Having looked at improper integrals last time, let’s look at some questions we’ve had involving integrals that either look improper but aren’t, or are improper but were missed, or that have other issues with their interval of integration.
1: Improper at an endpoint? No, just indeterminate
We’ll start with a question from Amia in early March:
Hi Dr math ,
I have the question below, and I want to know if I use limit in computing it or not, because I see it improper.
He’s right that, when \(x=0\), the integrand is undefined, because it requires division by zero: $$\require{AMSmath}\frac{-x}{(x+1)-\sqrt{x+1}}\bigg\rvert_{x=0}=\frac{-0}{1-1}=\frac{0}{0}.$$ So we can’t evaluate it there. And the limit will work; but is it necessary? Amia evidently recognizes that something is a little different here.
I answered, slightly missing the mark, as we’ll see:
Yes, as it is written, it is improper, and you technically need the limit (though I would not use 0 – ε; I’d use 0 + ε, in order to take the limit as x approaches 0 from the right). And you can certainly carry out all the work using the limit without difficulty.
But when I solve it, I find that the integrand simplifies quickly (in my case, after a substitution), and becomes defined at x=0, so it is no longer improper. So the limit is not really needed in the end.
In fact, the integrand actually has a removable discontinuity (which has the form 0/0 at x=0), and one point has no effect on the integral, so there is no problem once we remove it.
We’ll see below that I was wrong in calling it improper. But the limit is needed … sort of!
Here is my work, making the substitution \(u=\sqrt{x+1}\) (so \(x=u^2-1\), and \(dx=2udu\)), while ignoring whether it is improper: $$\int_0^1\frac{-x}{(x+1)-\sqrt{x+1}}dx=\int_1^{\sqrt{2}}\frac{1-u^2}{u^2-u}2udu\\=\int_1^{\sqrt{2}}\frac{(1-u)(1+u)}{u(u-1)}2udu=\int_1^{\sqrt{2}}-\frac{2u(1+u)}{u}du=\int_1^{\sqrt{2}}-2(1+u)du\\=-\int_1^{\sqrt{2}}(2u+2)du=-(u^2+2u)\bigg\rvert_{1}^{\sqrt{2}}=-(2+2\sqrt{2})+(1+2)=1-2\sqrt{2}$$
How did what felt like an improper integral lose its improperness? Is there more we should be thinking about? Was it really improper in the first place? Amia didn’t reply, so we didn’t have that further discussion.
But, as I mentioned, we could instead remove the removable discontinuity in the integrand itself, right at the start, removing any need for a limit:
$$\frac{-x}{(x+1)-\sqrt{x+1}}=\frac{-x}{(x+1)-\sqrt{x+1}}\cdot\frac{(x+1)+\sqrt{x+1}}{(x+1)+\sqrt{x+1}}\\=\frac{-x((x+1)+\sqrt{x+1})}{(x+1)^2-(x+1)}=\frac{-x((x+1)+\sqrt{x+1})}{(x+1)x}\\=\frac{-((x+1)+\sqrt{x+1})}{x+1}=-1-\frac{1}{\sqrt{x+1}}$$ This evaluates to \(-2\) for \(x=0\). Here is its graph:
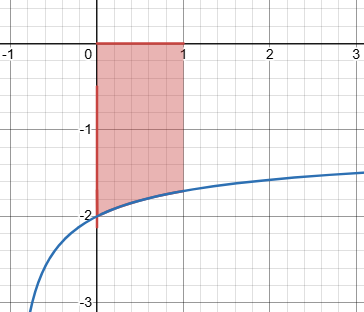
And we can easily integrate that:
$$\int_0^1\left[-1-(x+1)^{-1/2}\right]=-x-2(x+1)^{1/2}\bigg\rvert_0^1=(-1-2\sqrt{2})-(-2)=1-2\sqrt{2}$$
So clearly it is really not improper; you just have to “fill the hole” in the integrand. And since removable discontinuities in an integrand have no effect on the integral (whether it is in the interior or at an endpoint), that’s all perfectly legal.
Two integrals suspected of impropriety
2: Improper in the middle? No, just momentarily indeterminate
When I looked for earlier questions on improper integrals, I discovered that Amia had asked about the very same problem, seven years ago, in April of 2018. He first asked about another integral:
Is the integral improper?
I wanted to integrate the function (x-1) (1-(x-1)^6)^(1/2) on the interval [0,2]
I use substitution, I suppose u = (x-1)^2
du=2(x-1)dx ……. dx = du /(2(x-1))
When x=0 …. u=1
When x=2 …. u=1
Now the integration is: (1/2(x-1)) ∫ (1-u^3)^(1/2) .(x-1) on [1,1] = 0
My question: Can we divide by (x-1)?? (the value of (x-1)=0 when x=1 and x=1 belongs to the interval [0,2])
The integral in question is $$\int_0^2(x-1) (1-(x-1)^6)^{1/2}dx$$
After the substitution, he got $$\frac{1}{2(x-1)}\int_1^1(x-1) ((1-u^3)^{1/2}dx,$$ which is probably a typo; surely he didn’t think it valid to pull an expression containing the variable outside of the integral. I assume he really meant this:
$$\int_1^1\frac{1}{2(x-1)}(x-1) ((1-u^3)^{1/2}dx.$$
But even there, he has not completed the substitution.
His specific question is whether the \(x-1\), which becomes zero at one point within the interval, can be cancelled in the midst of his work. And what about those limits of integration both being the same after the substitution? There’s a lot to think about here.
Before we responded, he added another example of what he perceived to be the same issue (a seemingly improper integral), which I will hold for later to avoid confusion. That, as we’ll see, is the same problem we looked at above.
Doctor Fenton answered, first clarifying the meaning of “improper”:
Hi Amia,
An integral is improper if either it has a vertical asymptote in the interval of integration, or if the interval of integration is infinite. This function has no vertical asymptote (there is no factor of 0 in a denominator), and the interval of integration is finite.
You said,
I wanted to integrate the function (x-1) .((1-(x-1)^6)^(1/2) on the interval [0,2]
I use substitution, I suppose u = (x-1)^2
Good choice.
Improper integrals always involve infinity. This is what I failed to point out in my recent answer.
Amia presumably saw the integral as improper because there was a point within the interval where, in his work, he had to divide by 0; but that doesn’t make it infinite..
The substitution is a good choice because we see its differential, \(2(x-1)dx\), as part of the integrand.
You said,
du=2(x-1).dx ……. dx = du /(2(x-1))
I don’t recommend using the second differential [du /(2(x-1))], which mixes x and u. When you make a substitution u = g(x), and du = g'(x)dx, when you simplify all the x’s must disappear: an integral containing both x and u doesn’t make sense. Instead, you need to write
$$\int(x-1)\left(1-(x-1)^6\right)^{1/2}dx=\int\underset{(1-u^3)^{1/2}}{\underbrace{\left(1-(x-1)^6\right)^{1/2}}}\cdot\underset{1/2\,du}{\underbrace{(x-1)dx}}=\frac{1}{2}\int(1-u^3)^{1/2}du$$
I have seen teachers use such mixed differentials temporarily, but I avoid that. I’d do just what Doctor Fenton does, recognizing du as part of the integrand, rather than solving for dx. Note that no division is needed, because we just incorporate \((x-1)\) into \(du\).
You can see both Doctor Fenton’s style, and a Math Doctor using the ‘mixed differential” style, at Integration: Choosing a Substitution to Try.
You said,
when x=0 ….u=1
when x=2….u=1
so both limits of integration are 1, and you are integrating over an interval of length 0. Do you know what that gives?
That makes the integral zero, which he mentioned in his work (and may be the reason he didn’t fully carry out the substitution). We’ll be looking at another integral where this happens at the end of this post.
You said,
now the integration is: (1/2(x-1)) * the integration of (1-u^3)^(1/2) .(x-1) on [1,1] =0
As I said, an integral with two variables makes no sense here, so unless you can get rid of all the x’s, you have chosen the wrong substitution. However, in this example, the factors of x-1 in the numerator and denominator do cancel, leaving only an expression in u in the integrand.
Incidentally, you cannot find an elementary function antiderivative for this integrand, but you can evaluate the definite integral.
When you are trying to evaluate a definite integral, and it looks hard to find an antiderivative, it’s a good idea to check whether the interval might be carefully chosen to make things cancel out.
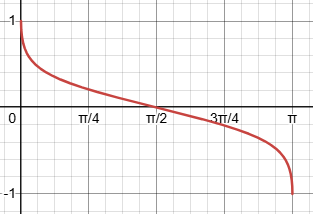
Here is what the integrand looks like:
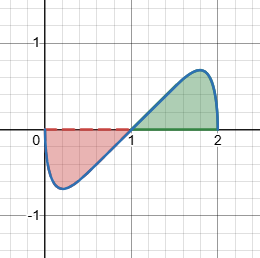
It should be obvious that the integral (over its entire domain) will be zero, because of its symmetry; the negative part cancels the positive part. The fact that the integrand is an odd function of \((x-1)\) is what makes this work.
1, reprise: Not improper, but indeterminate
Here is Amia’s second example, which is our first problem from above:
For example: if
f(x) = -x /((x+1)-sqrt(x+1))
and I wanted to integrate f on [0,1], it is improper integral, but if I use substitution
u = sqrt(x+1),
the integration becomes:
-2(1+u) on [0, sqrt(2)]
Is this method acceptable?
Another question: Can I use substitution to transform improper integral to proper integral?
As we saw, that substitution takes \(\int_0^1\frac{-x}{(x+1)-\sqrt{x+1}}dx\) to \(-2\int_1^{\sqrt{2}}(u+1)du\), which is proper.
So here, the substitution eliminates the division by zero.
Doctor Fenton’s answer continued to this problem:
You also ask about
For example: if f(x)= -x /((x+1)-sqrt(x+1)) on [0,1] and I wanted to integrate f on [0,1], it is improper integral, but if I use substitution u = sqrt(x+1), the integration becomes: -2(1+u) on [0, sqrt(2)].
Is this method acceptable?
That is not what I get. Could you show me your computation for this integral?
Amia showed his work:
I upload my solution below:
He did this a little differently than I did above, first finding an antiderivative in terms of x, and then evaluating the definite integral as an improper integral (using a limit), which as we’ve seen is not necessary.
Doctor Fenton responded:
Hi Amia,
That is correct. I don’t remember what I thought was different.
You could also work the problem without this substitution, by rationalizing the denominator:
$$\frac{x}{(x+1)-\sqrt{x+1}}=-\frac{x((x+1)+\sqrt{x+1})}{((x+1)-\sqrt{x+1})((x+1)+\sqrt{x+1})}=-\frac{x((x+1)+\sqrt{x+1})}{x^2+x}$$
which simplifies to
$$-\frac{(x+1)+\sqrt{x+1}}{x+1}=-\left(1+\frac{1}{\sqrt{x+1}}\right)$$
which is straightforward to integrate.
This is the same alternative work I did above.
Incidentally, this integral is not improper. Although the integrand is undefined at x=0, the left endpoint of the interval of integration, it does have a finite limit as x->0, so the integrand is not unbounded. It is usually assumed that the integrand is defined at x=0 so that the extended function is continuous.
This is where I was a little wrong in my answer: nothing becomes infinite, and filling in a “hole” is not the same as an improper integral.
3: Indeterminate at the last step? Rewrite it!
Another question, from 2022, is about an improper integral that was missed, though that’s not the main issue:
Can you please tell where am I going wrong here. Further evaluating it my answer is coming out to be infinity. But the correct answer is log 2
It appears that the problem is to integrate $$\int_0^{\pi/2}\frac{\cos(u)(1-\sin(u))}{\cos^2(u)}du.$$
Sheena immediately canceled cosines and wrote the integrand in terms of secant and tangent, using known formulas for the integrals. Looking at it now, three years later, I see a different approach that could have been taken: Rewrite the denominator and cancel in a different way: $$\frac{\cos(u)(1-\sin(u))}{\cos^2(u)}=\frac{\cos(u)(1-\sin(u))}{1-\sin^2(u)}\\=\frac{\cos(u)(1-\sin(u))}{(1+\sin(u))(1-\sin(u))}=\frac{\cos(u)}{1+\sin(u)}$$ This can be integrated by the substitution \(v=1+\sin(u)\), so that \(dv=\cos(u)du\), with interval of integration \([1,2]\), leading to the integral $$\int_1^2\frac{dv}{v}=\ln(2)-\ln(1)=\ln(2).$$
But the question is about the work shown, so we have to deal with that. We can’t evaluate \(\log|\cos(u)|\) at the end, because it is infinite when \(u=\frac{\pi}{2}\).
And did you notice that dividing by \(\cos(u)\) is troublesome when \(u=\frac{\pi}{2}\)?
I answered:
Hi, Sheena.
The first thing to notice is that this is an improper integral: The integrand becomes infinite at the upper limit.
In particular, you can’t just plug in π/2 for u; if you do, you get log(∞) + log(0) = ∞ – ∞, which is indeterminate.
So treat this carefully as a limit.
But … you can avoid the hardest part of the work by simplifying your result before evaluating; then the limit will no longer be an indeterminate form. What can you do with the sum of two logs?
This is somewhat related to our latest post (particularly the last section):
Here is the work, using the limit: $$\int_0^{\pi/2}\frac{\cos(u)(1-\sin(u))}{\cos^2(u)}du=\lim_{b\to\pi/2}\int_0^b\frac{\cos(u)(1-\sin(u))}{\cos^2(u)}du\\=\lim_{b\to\pi/2}\int_0^b(\sec(u)-\tan(u))du=\lim_{b\to\pi/2}\Bigl[\ln|\sec(u)+\tan(u)|+\ln|\cos(u)|\Bigr]_0^b\\=\lim_{b\to\pi/2}\Bigl(\ln|\sec(b)+\tan(u)|+\ln|\cos(b)|\Bigr)-\Bigl(\ln|\sec(0)+\tan(0)|+\ln|\cos(0)|\Bigr)\\=\lim_{b\to\pi/2}\Bigl(\ln|\sec(b)+\tan(u)|+\ln|\cos(b)|\Bigr)$$
That really changes nothing, except to remind us we are taking a limit, and can’t just plug in \(\frac{\pi}{2}\).
But when a limit has indeterminate form, we try to rewrite it so it is not indeterminate. Using the fact that \(\log\left(ab\right)=\log(a)+\log(b)\), we rewrite \(\ln|\sec(b)+\tan(u)|+\ln|\cos(b)|\) as $$\ln\Bigl|(\sec(b)+\tan(u))(\cos(b))\Bigr|=\ln\left|1+\sin(u)\right|$$ and the limit is \(\ln(2)\).
4: Why is it zero? Another vanishing interval
Let’s close with another example with interesting things happening at the limits. This is from Amia again, in April:
Hi Dr math,
I have the question solved below.
And I’m asking why the answer is zero?!
It is because integration on a point??
The substitution this time (like integral #2 above) transforms both limits of integration to the same point, reducing the interval to that one point. How does that happen?
Doctor Rick answered:
Hi, Amia.
“… because integration on a point ??”
Essentially yes. One of the basic properties of definite integrals is that
∫aa f(x)dx = 0
I was not entirely comfortable with the solution, but thinking it through, I see that it is valid. In substitution, in this case sin(x) = t2, the new variable (t) must be a function of the original variable (x), but it need not be a one-to-one function. We only need to be able to find t values corresponding to given values of x (in particular the limits of integration), not to find (a unique) x corresponding to a given t.
I also gain confidence by seeing another way to get the same answer! I notice that the integrand is an odd function when shifted by π/2, that is, f(π/2 + x) = –f(π/2 – x). Thus the integral over any interval symmetric about x = π/2 will be zero.
We’ll see this symmetry in a moment!
I joined in with some added thoughts on that “discomfort”:
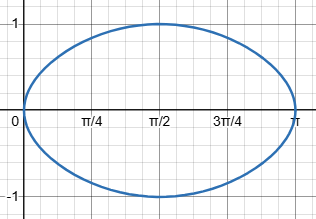
I agree that the integral is 0; here is the integrand:
The symmetry determines that.
That is, the areas above the axis on the left, and below the axis on the right, cancel out, leaving an area of zero. So the answer does make sense.
But it troubled me that the last line of your work doesn’t depend on the integrand! So the method still seemed suspect to me.
Here is the substitution you are making, sin(x) = t2 (x horizontal, t vertical):
So this is not only not one-to-one; it is not a function, as stated. But by taking a square root and thus assuming t is positive, t became a function of x:
One potential issue is that you didn’t define the substitution as a function of x; but ultimately you treated it as t = √sin(x), so that is okay. (I recommend explicitly stating this function; in trig substitution the same issue arises and can cause errors, because it is initially stated with x as a function of θ, and eventually you need the inverse.)
The fact that it is not one-to-one means that, ultimately, your integral is not literally “integration on a point”, but that the definite integral takes t from 0, to 1 (when x = π/2), and back to 0 corresponding to a different value of x. So if we found the antiderivative of your integrand in t, we would be evaluating it over a path that starts and ends at t=0, which is the reason for the answer of 0.
The issue with trig substitutions is that they are done in reverse to the usual “u-substitution”, not defining a new variable, typically u, as a function of the original, x, but rather replacing the original variable, x, with a function of a new variable, typically θ. Since, as Doctor Rick pointed out, the new variable must be a function of the new variable, we must define θ as a function of x by means of an inverse trig function. For example, when we let \(x=\sin(\theta)\), there are infinitely many values of θ that could work; it is not inherently a function of x, because the sine is not a one-to-one function. We need to keep in mind that we are really saying \(\theta=\sin^{-1}(x)\). And that memory is why using a function that is not one-to-one made me nervous!
I can’t think of an example of how this can cause trouble, but may add one later when I run across it!
Back to our problem, as x increases from 0 to π, t first rises to 1, and then falls back to 0. The integral is not all happening at one point, but (like a trip up a mountain and back) the net effect measured by the integral is as if we stayed at the bottom: We have not moved at all.
Let’s do the unnecessary, and actually find that antiderivative! I’ll make the substitution \(u=1+t\), so \(du=dt\):
$$\int\frac{2tdt}{(1+t)^2}=\int\frac{2(u-1)du}{u^2}\\=\int\left(2u^{-1}-2u^{-2}\right)du=2\ln(u)+2u^{-1}=2\ln(1+t)+\frac{2}{1+t}$$
And going back to the original variable, replacing \(t=\sqrt{\sin(x)}\), we get $$2\ln(1+\sqrt{\sin(x)})+\frac{2}{1+\sqrt{\sin(x)}}$$ Here is its graph (in green):
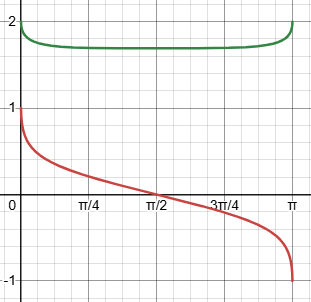
I also noticed, in experimenting with other substitutions that are not one-to-one, particularly an even function such as x = u2, that an integral over a symmetrical interval typically is zero because the integrand itself, when such a substitution helps, is odd. I don’t know how general that is, but it’s an interesting observation!
This is only a minor clarification, and only helps me feel more confident about what Doctor Rick said.
In our example, we would need to shift everything left by \(\frac{\pi}{2}\) to make it odd, with a symmetrical interval of integration; then the observation applies.

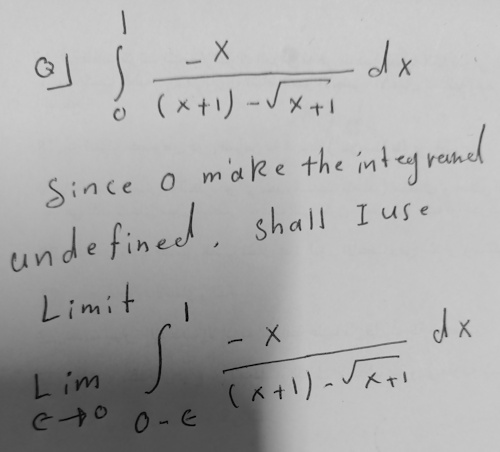
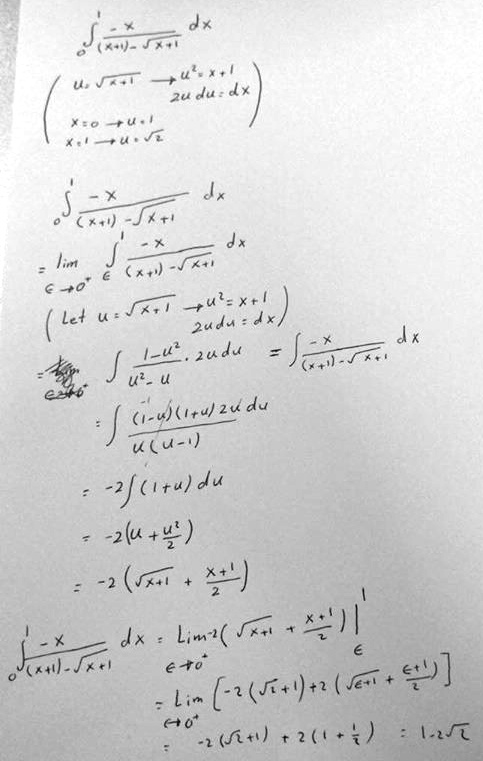
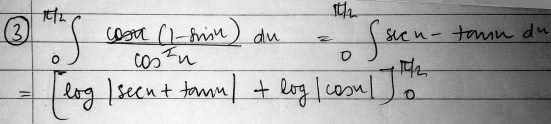

Pingback: Sign Issues in Integration – The Math Doctors