We’ll work through a textbook exercise that encourages students to discover what it’s like to invent a new number system, as well as why some ideas work but others do not. The topic: What would happen if we changed the definition of the imaginary unit i so that its square is 1 rather than -1?
Sometimes I don’t make a post from an otherwise good question, because the discussion got too long and complicated, editing would be too hard, and we have too many other good questions to publish. Here we have a wonderful exploration that seems worth the effort three years later.
An unusual exercise
The question came from Jitender in March 2022; he was asking in part about other people’s answers on a different site, where they weren’t careful to find out what the question really was (as we try to do), which led to confusion. I’ll be extracting only the most useful parts, and ignoring various wrong answers along the way. Here is the central question:
In the book of Bernard Johnston, titled: Numbers and Symmetry: An Introduction to Algebra; in section 1.1, Q.3 he states.
Suppose we defined i2 to be 1 rather than -1.
Describe the effect of multiplication by i in this situation in geometric terms.
Describe the effect of multiplication by 1 + i in geometric terms.
Attempt:
The usual meaning is that i2 lies on negative x-axis, i.e. (−1, 0). Also, i lies on y-axis.
When i2 lies on positive x-axis instead, the square root of i2 is ±i. So, i = ±1.
So the multiplication by i is now ambiguous as i is both 1, −1.
So such definition of i2 cannot be used.
The problem is definitely unusual, and requires some experience with abstract algebra (which is all about “what if”), and a willingness to set aside what one knows. This will not be “your father’s complex numbers”!
I answered:
I have several things to say.
First, the question is an odd one. To me,
Suppose we defined i2 to be 1 rather than -1. Describe the effect of multiplication by i.
is too much like
Suppose we defined 1+1 to be 1 rather than 2. Describe the effect on arithmetic.
The answer to that question is that everything would be different. You can’t just change the meaning of something. But something more is expected!
But, of course, this question is deeper than that; it is about changing one point in the definition of complex numbers.
I pointed out that those who had answered him on the other site should have asked about the context; I found it:
Here is what I see in the book (as I found it in Google):
The exercises:
(What you called question 3 is question 6 in this edition.)
What he had said about i2:
This first chapter is introducing the idea of abstract algebra by demonstrating the creation of “new kinds of numbers”, starting here with Gaussian integers (complex numbers with integer components). This idea of inventing a new number, i, and then picturing it as lying on an axis perpendicular to the real number line is explored in Making Sense of Imaginary Numbers. But whereas there we start with the goal of finding square roots of negative numbers, here he starts abstractly, just treating each point on a plane with integer coordinates as a “number”, and inventing operations of addition and multiplication. This comes down to the question of what \(i^2\) should be.
The author is approaching the concept of complex numbers purely through the geometric model, making some arbitrary choices and considering the consequences. Presumably he wants you to do the same sort of thinking he has demonstrated, and to conclude that i2 = 1 does not produce a useful structure.
My own first thought was simply that it would make i just another name for either 1 or -1 (both of which have 1 as their square), and therefore not useful! But that’s not the perspective he tells you to take.
As for your own answer, ambiguity is not the issue, as there are two square roots of anything, in the “usual” scheme.
The exercise tells you exactly what to do: Try multiplying several numbers by i, as he did with (3 + 5i)(6 – 2i), but starting, say, with (2 + 3i)i and so on, and then move on to things like (2 + 3i)(1 + i). What geometric effect does each multiplication have? Draw it out, and see if you can describe it in words.
The key to the exercise is to feel free to experiment, trying things that may not make sense, until, hopefully, they will! (Spoiler: They won’t, really.)
Starting to explore
Jitender replied:
(2 + 3i)i = 2i + 3i2 = 2i + 3, i.e. a reflection across the line y = x, of line 2 + 3i.
Continuing with (2 + 3i)(1 + i) = 2 + 5i + 3i2 = 5i + 5.
The modulus of 1 + i = ✓(1 + i2) = ✓(1 + 1) = ✓2.
The modulus of 2 + 3i = ✓(4 + i2.9) = ✓13.
The modulus of 5i + 5 = 2✓5.
Even, (✓2)2 + (✓13)2 ≠ 50.
He has a geometric description of one example of multiplication by i, then an unsuccessful attempt to analyze one example of multiplication by \(1+i\).
I answered, first about his first calculation:
Yes, that is what he is saying to do: You tried multiplying one particular number by i. And, yes, it is a reflection, rather than a rotation. Interesting! This suggests there may actually be something worth exploring.
In order to answer the actual first question, “Describe the effect of multiplication by i in this situation in geometric terms”, you need to try multiplying other numbers by i; presumably, you have already observed that the reflection in y = x is a general characterization of multiplication by i, not true only in the one example you have tried. Good.
One example is not enough to be sure of general behavior. We could generalize this by multiplying any number \(a+bi\) by i: $$(a+bi)i=ai+bi^2=b+ai$$ which is, in fact, a reflection over the line \(y=x\), from the point \((a,b)\) to the point \((b,a)\).
As to the second calculation:
You’ve found the result of multiplying one particular number, 2+3i, by 1+i, and I suppose you are trying to find some connection of the result with the original, by comparing the modulus of the factors and the product. That’s one try, and it didn’t produce any results, did it? So look for other connections. (You are, apparently, meant to be simulating the way new math is invented, which requires perseverance.)
What I would do is to find the products of several different numbers by 1+i, making a table and graphing the pairs in hope of seeing a pattern. One way to graph this would be to treat each “complex number” as a point on the plane, and draw an arrow from the input point to the output point (e.g. from(2, 3) to (5, 5), and repeat for other numbers.
You’ll find something interesting (which is also a good reason not to define multiplication this way!). You’ll then want to think about why that happens. To figure this out, you might want to make a general formula for (a + bi)(1 + i).
If you wanted to continue beyond what you are explicitly asked for, you might think about a general description of what this “multiplication” does in general, and consequently what these “complex numbers” really represent, which will vindicate my initial impression of them.
As we proceed, we’ll be seeing more examples, graphs, and general formulas; you, the reader, may want to try the same!
I put “complex numbers” in quotes, because they are not really complex numbers as we know them; perhaps “pseudo-complex numbers” would be a better term.
Jitender replied:
I tried everything, even modulus of product and comparing. Also, tried assuming value of i. But, I never tried to give no meaning to i, but assign a meaning for i2. This approach made no sense to me.
Let the number. to be multiplied with 1+i be denoted as: x. Taking different values for x, get:
x = constant, say = 5. Then 5(1 + i) = 5 + 5i. Modulus of 1 + i = ✓2. Modulus of 5 + 5i = ✓(25+25) = 5✓2.
Modulus of 5 = 5.
Product of modulus of 5, 1 + i = 5✓2 = modulus of 5 + 5i.
So, modulus is conserved.
Regarding, forming a graph : if i is left undefined, then how to graph is not clear.
Only modulus is possible, as considers i2.
Neither angle of any number involving I can be stated.
Unfortunately, he is trying every approach to thinking about the problem except what he was explicitly told to do. I see this in other students who have learned routine ways to do everything, and have trouble letting go and just experiencing the unknown. I tell them, Just try it, and see what happens!
I replied to the first paragraph,
Did you not notice that what the author did was to assume a quantity called “i” without giving it any meaning other than being a point on the plane, and defining only what i2 is?
What the author did for the actual i, is also what needs to be done here. What we mean by i is merely the point \((0,1)\), and nothing more. What we are exploring is the implications of a tentative definition of an operation.
Then, for the rest, rather than having “tried everything” …
You are trying too little.
Try multiplying many “complex numbers” by 1+i, not just one more real number, 5! I told you how important it is to persevere; and surely you know that a pattern can’t be seen from just one or two examples.
Try multiplying all of these by 1+i: -2, -1, 0, 1, 2; -2+i, -1+i, 0+i, 1+i, 2+i; -2+2i, -1+2i, 0+2i, 1+2i, 2+2i; and more if you want.
And don’t think about the modulus; that will not necessarily help at all. Look at the entire number you get. You may not need to graph them, but I think it will help.
And you were told how to graph it! Your i should still be at (0, 1), where the author put it long before this exercise. Without doing that, what geometrical interpretation could he possibly expect? If you don’t think there is any geometry that the question could be asking about, that should have been your first question of me. All he is telling you to change is the choice of a value for i2; everything else should be unchanged.
Jitender reported these results:
-2(1+i) = -2-2i (-2+i)(1+i) = -1- i (-2+2i)(1+i) = 0 -1(1+i) = -1-i (-1+i)(1+i) = 0 (-1+2i)(1+i) = 1+i 0(1+i) = 0 (0+i)(1+i) = 1+ i (0+2i)(1+i) = 2+2i 1(1+i) = 1+i (1+i)(1+i) = 2+2i (1+2i)(1+i) = 3+3i 2(1+i) = 2+2i (2+i)(1+i) = 3+3i (2+2i)(1+i) = 4+4i
I’ve omitted comments he made on each individual result, which “missed the forest for the trees”.
I commented:
Don’t just look at each one individually; you are looking for a pattern. That’s also why my suggestion of a graph would be helpful, if you would try it.
Do you notice, first, that many of these products are equal, and, second, that they are all very similar? Please open your eyes and look!
If you still don’t see it, then plot these on the complex plane, and observe where they all are.
And if you still don’t see the pattern, find the general formula for (a + bi)(1 + i), and compare with the table.
Keep observing and thinking. The point of this exercise is to give you some experience thinking like a mathematician, which is a new experience for you, so it will take time. It’s a far better exercise than my original impression.
What do you get in general, for (a + bi)(1 + i)? Can you describe that fully in a few words?
I also pointed out that it’s possible to get a product of zero when neither factor is zero; real numbers don’t have such “zero-divisors”, which can make a number system hard to use. (To be precise, the number system we are exploring is not an integral domain, so it will behave in many strange ways.)
The result I asked for is simple: $$(a+bi)(1+i)=a+ai+bi+bi^2=a+ai+bi+b=(a+b)+(a+b)i$$
I added:
Another way to say it is that the real and imaginary parts are always equal, and specifically equal to the sum of the components of the given number. Had you noticed this previously, from the examples?
Now, what does multiplication by 1 + i do to any number a + bi, in geometric terms? That is what they are asking for. (And this is where graphing the effects, as I have suggested from the beginning, can help.)
When that didn’t elicit the answer I was looking for, I added,
How about answering some more specific questions:
Geometrically, where do you always find the result of the multiplication?
And where do you find the numbers z whose product with 1+i has a given value, say r(1+i)?
Some words like “line” may be useful. That’s what we mean by “geometric”.
The geometrical perspective
Eventually, I answered my own questions:
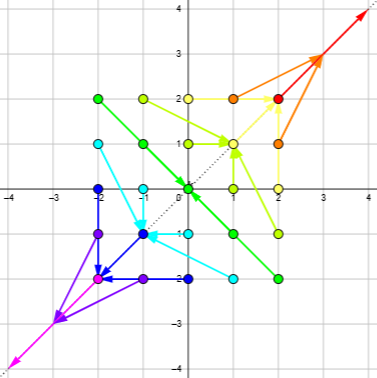
Here is a graph such as I have described before, with each arrow starting at one of 25 points, and its head at the product of that number with 1+i:
For example, one of the orange arrows shows that multiplication by 1+i takes (2+i) to 3+3i.
In contrast, here is what you would get for multiplication of actual complex numbers by \(1+i\), which rotates each point by 45° and dilates it by \(\sqrt{2}\):
For example, $$(2+i)(1+i)=2+2i+i-1=1+3i$$
Here I changed the coloring to represent the distance from the origin, because absolute value plays a central role here. Our pseudo-complex numbers have a different effect, which we want to understand.
My first question was about the locus of all the arrowheads (products), and my second question was about the locus of all tails of arrows whose heads are in a given place (such as 3+3i). The answers to both questions are suggested by features of my graph.
That is, the first question, about where the products are, is about the range of the function \(f(z)=(1+i)z\), and the second question is about the preimage of any given point.
The book’s question is asking for a way to describe what every arrow does, described geometrically. I’m not sure just what sort of description they expect; they might be satisfied with the answer to my first question, or they may want something more, for which my questions may suggest some ideas. I have one idea of a nice way to say it, using terms like “line”, “projection”, and “dilation” or “stretching”.
After further attempts to elicit a geometrical description, I gave the answers:
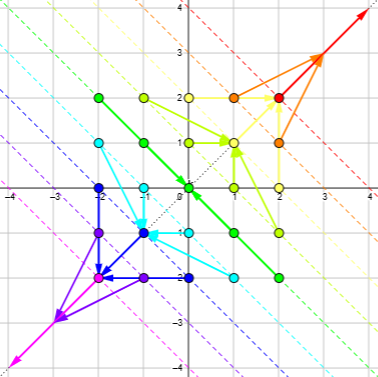
The answer to question 1 is that the product always lies on the line y = x; that is, it is a multiple of 1+i. You have essentially said this, without saying it explicitly.
One important implication of this is that the function f(x+yi) = (x+yi)(1+i) is neither one-to-one nor onto (an injection or a surjection), which is one good reason not to define multiplication of complex numbers in this way. It doesn’t behave like a multiplication should.
We expect the function \(f(z)=cz\), for any constant multiplier c, to yield a different answer for each input (a one-to-one function). And we expect to be able to get any number as a product.
The answer to question 2 is that the set of numbers that are transformed by multiplication into (r, r), that is, r+ri, lie on the line x+y=r.
So the product of all numbers on such a line are transformed into the same number.
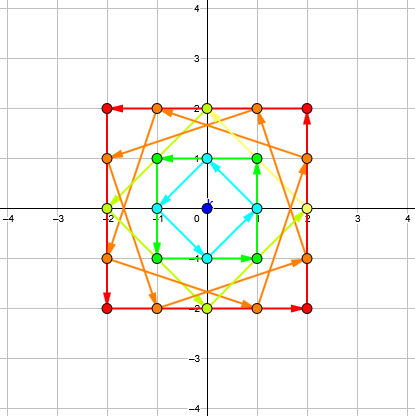
Here I have drawn the locus of products (black broken line, barely visible) and the locus of numbers that are transformed into each distinct product (colored broken lines):
Numbers on each colored broken line are equivalent under this multiplication; the function does not distinguish them.
Here is the same sort of graph, for multiplication by i:
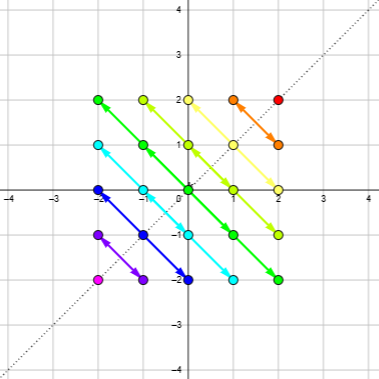
As we saw, this reflects each point across the line \(y=x\). This is less peculiar; but we still see that every point on one of those diagonal lines moves to a point on the same diagonal line. (That is, the product is a function only of the sum of the components.)
For contrast, here is multiplication of actual complex numbers by i:
This is a rotation by 90°, and leaves the absolute value unchanged.
My answer to the book’s question is this:
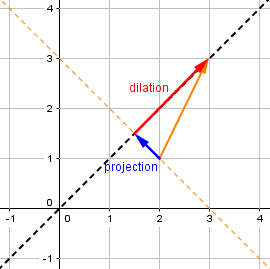
The transformation f(z) = f(x+yi) = (x+yi)(1+i) projects z perpendicularly onto the line y=x (along one of the colored lines) and then dilates by a factor of 2.
The multiplication, that is, squashes the entire plane onto a line, and then stretches it.
For example, here is the transformation for 2+i:
Multiplication by i, as we saw, flips a point entirely across the line, with no stretch.
The result is that multiplication by 1+i is effectively a matter of treating all “complex” numbers as a single number line, on which multiplication by 1+i is equivalent to multiplication by 1+1 = 2. (I presume something similar could be said of other multiplications.)
It isn’t quite that simple, but sort of.
This is related to my original sense (and perhaps yours) that this “i” is, for practical purposes, just another name for 1 (even though we can’t say it is 1). We don’t have a fully two-dimensional number system. The actual complex number system, in which multiplication transforms by rotation and dilation, and is therefore one-to-one, is far more interesting and useful.
And that is presumably the point of this very open-ended problem.
Expanding the exploration
After discussing this, Jitender tried multiplying by a general number \(a+bi\), but couldn’t see a pattern. This didn’t get very far, but we can look at it a little here, from a perspective we didn’t get to.
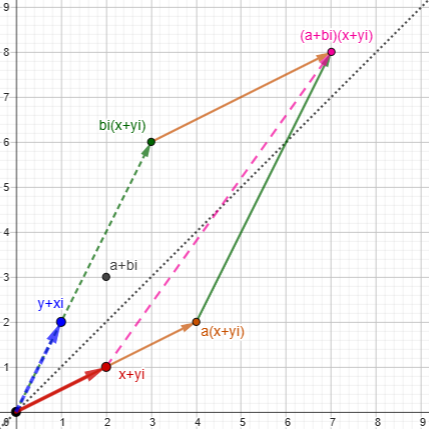
First, we can write the product as $$(a+bi)(x+yi)=ax+ayi+bxi+byi^2=ax+ayi+bxi+by=a(x+yi)+b(y+ix)$$
In terms of vectors, we are multiplying \(\left<x,y\right>\) by \(\left<a,b\right>\) to get the sum of a times \(\left<x,y\right>\) and b times \(\left<y,x\right>\).
So the “real” part multiplies the vector itself, and the “imaginary” part multiplies its reflection in the line \(y=x\). Here is \((2+3i)(2+i)=7+8i\):
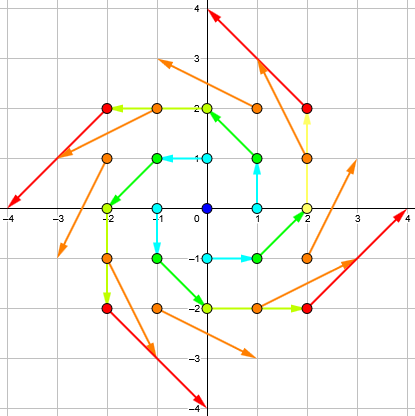
Here is what it looks like to multiply our set of 25 numbers by \((2+3i)\):
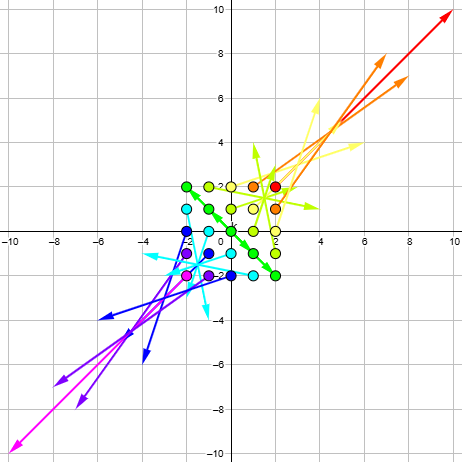
And here we multiply by ((2-3i)\):
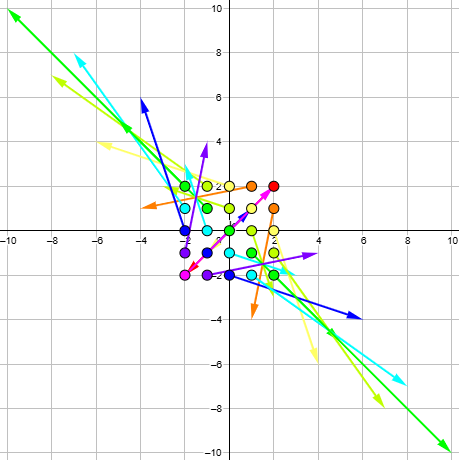
There are probably many more ways to describe what this does, and more questions to raise. But the main point seems clear: This would not be a useful type of number to invent, as interesting as it might be to explore!