We have a question about an improper integral, where one is strongly tempted to take a shortcut that makes it convergent, though the proper definition does not. Why can’t we do this? We’ll see something of the freedom mathematicians have in the matter of definitions, as well as why the standard definition has to be what it is.
Improper integrals: review
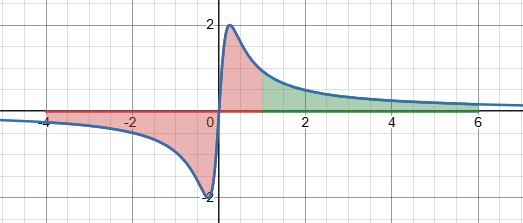
An improper integral is one that either has an infinite limit at either or both ends, such as \(\int_1^\infty \frac{1}{x^3}dx\), or whose integrand becomes infinite at either or both limits, like \(\int_0^3 \frac{1}{x}dx\), or somewhere in between, like \(\int_0^3 \frac{1}{x-1}dx\). We’ll start out looking at this latter example. Here is a graph of that integral:
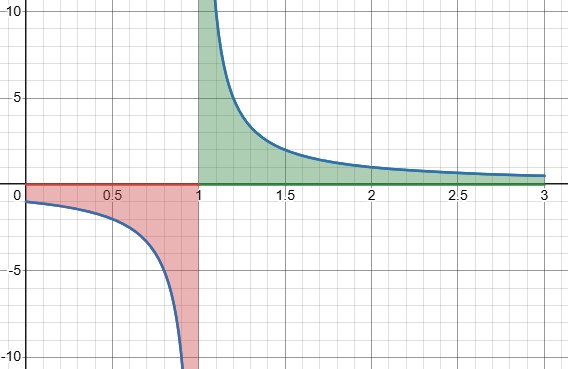
The integrand becomes infinite at \(x=1\), so we can’t literally add up slices to find the total area. Instead, we integrate up to some point short of the discontinuity, and take the limit as that point approaches 1, like this:
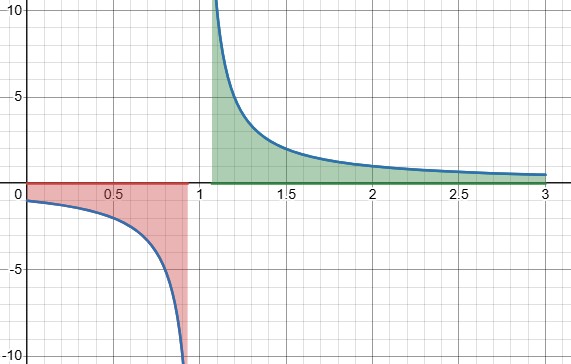
Sometimes the limits will exist; sometimes they do not, and we say the integral diverges.
(The green part above will be positive, and the red part is negative. Do you see an interesting possibility?)
Why can’t I combine the limits?
The question came from Sudeep in March, starting with a textbook example and the student’s own work:
When solving for the improper integral, if we were to solve for both parts of the integral, by taking different limits for both parts. Like as limit as t approaches 1 from the negative side and when s approaches 1 from the positive side. Now at the last step if I introduce 1-epsilon = t and 1+epsilon = s, would it become ln(1) which is zero so the solution is ln(2). Or is there some kind of mistake in those steps or approaching the problem like that. Also from the book solution. They say because the first integral is divergent the second one also must be divergent and therefore the whole integral is divergent. I am having trouble in understanding which one is true. Cause wouldn’t the integral have a finite value if you both integrals are essentially the same and are opposite of each other?
The author takes two separate limits, and finds that one of them doesn’t converge, so he gives up. (If he worked out that second limit, it, too, would diverge; but since both have to converge in order to have an answer, he doesn’t need to do that.)
Sudeep starts out following the book, but then wants to combine the two limits into one, by expressing both s and t in terms of one variable ε. If he does that, the rest of the work looks like this: $$\lim_{\epsilon\to0}\ln\left|\frac{-\epsilon}{\epsilon}\right|=\lim_{\epsilon\to0}\ln(1)=0,$$ so the answer is \(\ln(2)\).
You’d get the same answer if you just ignored the improperness altogether: $$\require{AMSmath}\int_0^3\frac{dx}{x-1}=\ln\left|x-1\right|\bigg\rvert_0^3=\ln|2|-\ln|-1|=\ln(2)-\ln(1)=\ln(2)$$
So why does the book insist that the integral is divergent?
A matter of definition
I answered:
Hi, Sudeep.
You said,
They say because the first integral is divergent the second one also must be divergent and therefore the whole integral is divergent.
No, that isn’t what they say. They say that because one is divergent, the entire integral is divergent – even if it should turn out that the second was convergent!
This is the definition of this sort of improper integral: The integral is the sum of two separate limits, and it converges only if both parts individually converge.
Here is a textbook definition that makes it explicit:
Paul’s Online Notes: Section 7.8 : Improper Integrals
Example 7 which follows this is much like yours:
You said:
Now at the last step if I introduce 1-epsilon = t and 1+epsilon = s, would it become ln(1) which is zero so the solution is ln(2). Or is there some kind of mistake in those steps or approaching the problem like that.
What you are doing in that last step is to take both limits simultaneously, using the same epsilon, so that you are approaching from both sides at the same rate. This is not allowed, just as it is not allowed to take limits going to \(\infty\) and \(-\infty\) at the same rate.
There are cases like this where you can make a case for a finite value for the integral, but it just doesn’t fit the definition. The limits must be approached independently.
This is where most textbooks I’ve seen leave it: Just do as we say, because this is the definition. But that isn’t very satisfying, is it?
But why must it be that way?
Sudeep had a further question:
Thank you Dr. Peterson for your reply.
I now understand the book’s approach.
But could you explain why it’s not allowed to substitute the limits from t and s to just epsilon. So that I can take the limit epsilon approaches 0 and then solve the limit. Is there no mathematical law that allows us to do that?
Good question!
I replied:
I spent some time looking for a source that would discuss this issue in detail, either in your case (an interior infinite discontinuity), or in the case of an integral from -∞ to ∞ (an infinite interval of integration). I was surprised not to find it readily.
(In fact, just now I checked my copy of Stewart to see if it says more, knowing it’s well respected, and found that that is your book! I was surprised to see that he emphasizes this issue less than the books I’d found online.)
Here is an example of an infinite interval, for which we need a separate limit at each end:
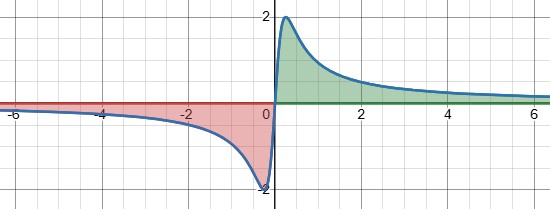
Typically we split this into two separate integrals: $$\int_{-\infty}^{\infty}\frac{16x}{16x^2+1}dx=\lim_{a\to-\infty}\int_a^0\frac{16x}{16x^2+1}dx+\lim_{b\to\infty}\int_0^b\frac{16x}{16x^2+1}dx$$
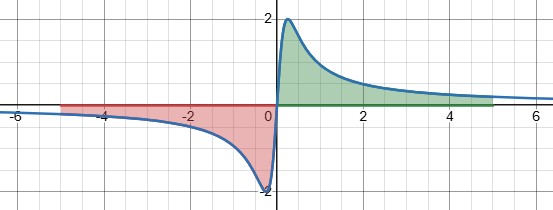
Each of these two integrals turns out to be divergent, so the entire integral is divergent.
What we can’t do is to combine it into one limit, like this: $$\int_{-\infty}^{\infty}\frac{16x}{16x^2+1}dx=\lim_{a\to\infty}\int_{-a}^a\frac{16x}{16x^2+1}dx$$
This, you may notice, would result in 0, even though the integrand is divergent, because this is an odd function and the red and green parts cancel..
But why? I gave two reasons.
So I’ll have to say a little more myself.
The idea is, first, that we need to define the integral as the sum of two integrals because that is a fundamental property of integrals: The integral from a to b, plus the integral from b to c, equals the integral from a to c. If that were not true, then it would break the rules for an integral. (It’s like the fact that if you cut a plane figure into pieces, the sum of their areas is the area of the whole.)
Then, if either part, calculated on its own, has “infinite area”, we can’t add them up, because infinities don’t work with arithmetic.
So if treating the integral as the sum of two different integrals (as the definition specifies) gives a different result (namely, undefined) than treating it as a single integral, both can’t be allowed.
But three’s more:
In your example, if you evaluate each integral, the first is \(-\infty\) and the second is \(+\infty\), and it just isn’t true that \(-\infty+\infty=0\); that’s an indeterminate expression.
“Indeterminate” means that you can get different answers depending on how you get there. As an example, you took t = 1-ε and s = 1+ε, resulting in
$$\lim_{t\to0^+,s\to0^-}\ln\left|\frac{t-1}{s-1}\right|=\lim_{\epsilon\to0^+}\ln\left|\frac{1-\epsilon-1}{1+\epsilon-1}\right|=\lim_{\epsilon\to0^+}\ln\left|\frac{-\epsilon}{\epsilon}\right|=\ln(1)=0$$
Suppose we make a small change and instead let t = 1-ε and s = 1+2ε. Then your answer becomes
$$\lim_{t\to0^+,s\to0^-}\ln\left|\frac{t-1}{s-1}\right|=\lim_{\epsilon\to0^+}\ln\left|\frac{1-\epsilon-1}{1+2\epsilon-1}\right|=\lim_{\epsilon\to0^+}\ln\left|\frac{-\epsilon}{2\epsilon}\right|=\ln\left(\frac{1}{2}\right)=-\ln(2)$$
rather than 0, so the integral becomes -ln(2) + ln(2) = 0 rather than ln(2). Approaching from the right slower than from the left changes the sum.
That’s why I pointed out that you were “approaching from both sides at the same rate“. Changing that changes the result. And that’s how indeterminate limits work. If the definition is to be consistent, it has to treat the two integrals separately, rather than let them interact in random ways.
Any time you can get two different answers by doing the same work different ways, something is wrong. This sort of definition can’t be allowed.
We can do it … if we give it a new name!
The next day, I happened upon a fuller answer:
While I was looking for a topic for a future post here, I discovered that we have an answer to your question (and more) on our old site, Ask Dr. Math (which is now accessible only with a free account).
Let’s take a look at that here. The question is from 2002, and deals initially with the infinite interval case:
Cauchy Principal Value Integral Why isn't an integral from negative infinity to positive infinity defined as the limit as t (or any other variable) approaches infinity of the integral from -t to t? In other words, why must we split an integral into two halves and evaluate each as a one-sided improper integral (as the standard definition of such an integral states)? For example, it would be intuitively pleasing for the integral of x^3 (or another odd function like x / (x^2+1), x, etc.) from negative infinity to positive infinity to be zero. Yet this integral diverges under the present definition because each side diverges! The fact that the sides are equal and opposite doesn't even come into play. This does not make sense to me. If someone has some insight into why mathematicians have defined integrals from negative infinity to positive infinity this way, I would greatly appreciate it if they would share their knowledge with me. I know there must be some good reason for it. Thank you.
Both of our examples so far are odd functions, which certainly look like the negative half cancels out the positive half. Why can’t it?
This example, \(f(x)=x^3\), is similar, but more troublesome, because each half more obviously has infinite area:
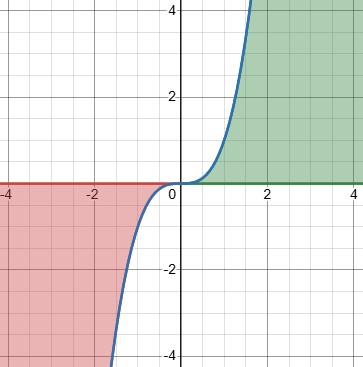
Here is the correct work for the integral: $$\int_{-\infty}^{\infty}x^3dx=\lim_{a\to-\infty}\int_a^0x^3dx+\lim_{b\to\infty}\int_0^bx^3dx=\lim_{a\to-\infty}\left[\frac{x^4}{4}\right]_a^0+\lim_{b\to\infty}\left[\frac{x^4}{4}\right]_0^b=-\infty+\infty$$ which is undefined.
(Yes, this is an indeterminate form, which can often be overcome; but as it results from taking two limits, rather than being part of the process of taking a single limit, there is nothing we can rewrite to make it possible to evaluate it: The sum has to be left undefined.)
But for any finite interval \([-t,t]\), the integral is clearly zero:
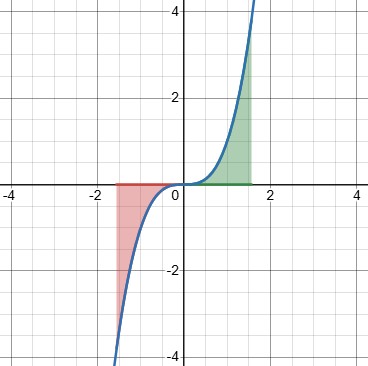
John, like Sudeep, wants to do this: $$\int_{-\infty}^{\infty}x^3dx=\lim_{t\to\infty}\int_{-t}^{t}x^3dx=\lim_{t\to\infty}\left[\frac{x^4}{4}\right]_{-t}^t=\lim_{t\to\infty}\left[\frac{t^4}{4}-\frac{(-t)^4}{4}\right]=\lim_{t\to\infty}0=0$$
Again, why can’t we allow this? Isn’t it good to turn something impossible into something possible?
Introducing the Cauchy Principal Value
Doctor Pete answered:
Hi John, Your question raises a very good point, one that is often inadequately discussed in undergraduate calculus courses. However, it is important to realize that what may make intuitive sense is not necessarily what is consistent with other mathematical concepts. In calculus, we must be careful in deciding what it really means to compute an improper integral, and more generally, the related notions of convergence and indeterminate forms.
Mathematical definitions usually are what they are because of experience; we find that if we defined a concept in any other way than what we do, then other things would stop working.
But should you feel like the type of improper integral you are describing does not have its own meaning or significance in mathematics, do not worry. You have just described what is known as the Cauchy principal value integral. There are essentially two types: the first is the doubly infinite improper integral, e.g.,for which the Cauchy principal value is defined as
Note, by the way, that this doesn’t require F to have any sort of symmetry; we are just taking symmetric limits. But it may be most useful in symmetric situations.
The second is where F has a discontinuity at some point c on the interval [a,b]. Then the improper integralhas Cauchy principal value
In both cases, the idea is to consider the improper integrals as limits that are symmetrically computed about the point of discontinuity (in the first case, the point of discontinuity is at infinity).
This is Sudeep’s case.
Why keep the two separate, rather than equate them?
Now Doctor Pete answers the big question:
In light of this, you are probably wondering why the improper integral itself is not defined to be the Cauchy principal value. After all, why talk about the two things as if they were separate? The simple answer is that they are indeed not the same thing at all. The key difference here is that the improper integral must satisfy a more strict criterion for convergence than the CPV, as required under the definition of integral as a Riemann sum. We need to distinguish these two things because not every function has a CPV integral, and those that do, do not necessarily have a convergent improper integral. So a distinction is made between the two because there are contexts in which it is inappropriate to give an integral a CPV, and others in which it is necessary.
So the Cauchy Principal Value is not really an integral, because we’re intentionally relaxing the rules. But sometimes it’s exactly what we need.
We have now arrived at the heart of your question: Why not give a function like F[x] = x^3 the Cauchy principal value when integrating over the entire real line? Well, the function itself increases (decreases) without bound as x tends to infinity (-infinity), and therefore talking about the value of the improper integral is like saying Infinity - Infinity = 0, which is not necessarily the case, as a discussion of indeterminate forms and L'Hopital's Rule would reveal. In fact, we don't even need to consider a function that is unbounded at infinity, only that the improper integral over a half-infinite subinterval is unbounded. Simply put, the symmetry of the function is unimportant in light of the fact that we are dealing with an indeterminate form.
He is referring to examples like those we used above, where the function itself was bounded (never became infinite), but the integral did, making the result an indeterminate form that couldn’t be resolved.
In our examples, the left half was negative infinity and the right half was positive infinity. They only cancel out to give 0 if we approach both infinities synchronously, so that the sum is never infinite.
Another way to look at it: What if you shifted the point at which you partition the real line? You would not want the value of the improper integral to depend on where you choose this point. And while it may be the case that there is an "obvious" choice for functions like F[x] = x^3, what about arbitrary polynomials of odd degree, which are not necessarily symmetric about the origin or any other point? It is pretty obvious that if you shift this point, the value of the improper integral will change. You could always choose to split the real line at the origin, but this merely amounts to computing the Cauchy principal value. Hence the CPV of doubly infinite integrals lacks a very important quality: independence from the underlying coordinate system. Therefore, we want to maintain a sufficiently strict interpretation of the improper integral so that when it exists, it is independent of the choice of limits of integration. Violation of this property is considered inconsistent with the development of calculus, more so than trying to preserve some aspect of symmetry in the integrand. That is the crux of the matter.
Here is what we get if we split the interval at \(x=1\) (that is, center our interval on 1 rather than 0):
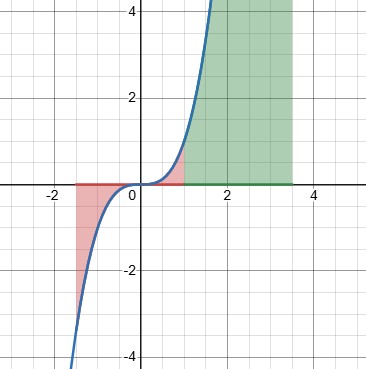
It certainly looks different; and indeed,
$$\text{“PV”}\int_{-\infty}^{\infty}x^3dx=\lim_{t\to\infty}\int_{1-t}^{1+t}x^3dx=\lim_{t\to\infty}\left[\frac{x^4}{4}\right]_{1-t}^{1+t}=\lim_{t\to\infty}\left[\frac{(1+t)^4}{4}-\frac{(1-t)^4}{4}\right]=\lim_{t\to\infty}\frac{8t^3+8t}{4}=\infty$$
rather than 0.
But this is the same as the PV (as properly defined) of \(x^3-1\), that is, our original integrand shifted right by one unit. How can an integral change when you just shift everything a little?
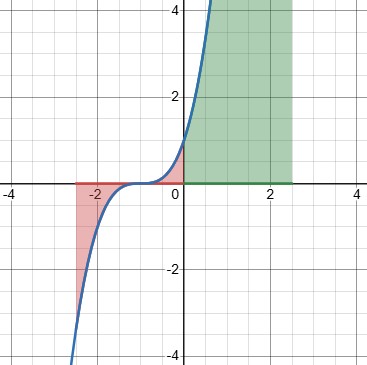
So the principal value integral changes when you shift the function! That’s not good.
Let’s do this with the example I made up earlier, again splitting it at \(x=1\):
$$\text{“PV”}\int_{-\infty}^{\infty}\frac{16x}{16x^2+1}dx=\lim_{t\to\infty}\int_{1-t}^{1+t}\frac{16x}{16x^2+1}dx=\lim_{t\to\infty}\left[\frac{1}{2}\ln\left|16x^2+1\right|\right]_{1-t}^{1+t}=\\\lim_{t\to\infty}\left[\frac{1}{2}\ln\left|16(1+t)^2+1\right|-\frac{1}{2}\ln\left|16(1-t)^2+1\right|\right]=\lim_{t\to\infty}\frac{1}{2}\ln\left|\frac{16(1+t)^2+1}{16(1-t)^2+1}\right|=\\\lim_{t\to\infty}\frac{1}{2}\ln\left|\frac{16(\frac{1}{t}+1)^2+\frac{1}{t^2}}{16(\frac{1}{t}-1)^2+\frac{1}{t^2}}\right|=\frac{1}{2}\ln\left|\frac{16}{16}\right|=0$$
So in this case, though it looks impossible at first glance, we do still get 0 with the offset. Why? This is normal for convergent integrals, but can also happen in the divergent case. Never assume anything in the presence of infinity!
Still, the CPV exists and is not without its uses, for example, in the computation of Hilbert transforms, or other more advanced topics in real and complex analysis. But it is not generally needed in elementary calculus, so it is not discussed. I hope I've answered your question to your satisfaction, long as my response may be. You've asked an excellent question, one that needs careful explanation and is not easily dismissed. If I may say so, it reveals your potential as a mathematician! If you want further clarification, or have any other questions, feel free to write.
I had forgotten whatever I may have learned about the topic, because I have not touched these fields in a long time; so we won’t try to go any deeper into it. The important thing is to know that there is something there – the idea was not irrational at all!
John answered:
Doctor Pete, Thank you very much for your answer. It was very clear and helpful (and I much prefer long responses to short ones!). I knew there was some important reason for defining an improper integral this way, and I now know that reason!
Many of the reasons he gave echo mine, but put into a clearer context.
I closed the current discussion:
Sudeep, I hope that helps. I expect to put this into a future post supplemented with graphs and examples. I think it will help many others.
While I was editing this post, Sudeep asked a different question that tied into this one in an interesting way (and affected some of what I’ve said here. We’ll get to that later.


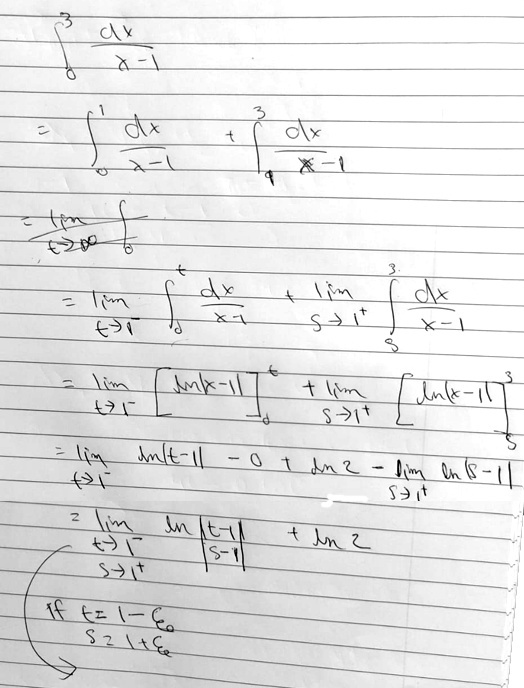


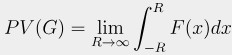
Pingback: When Is an Improper Integral Not an Improper Integral? – The Math Doctors