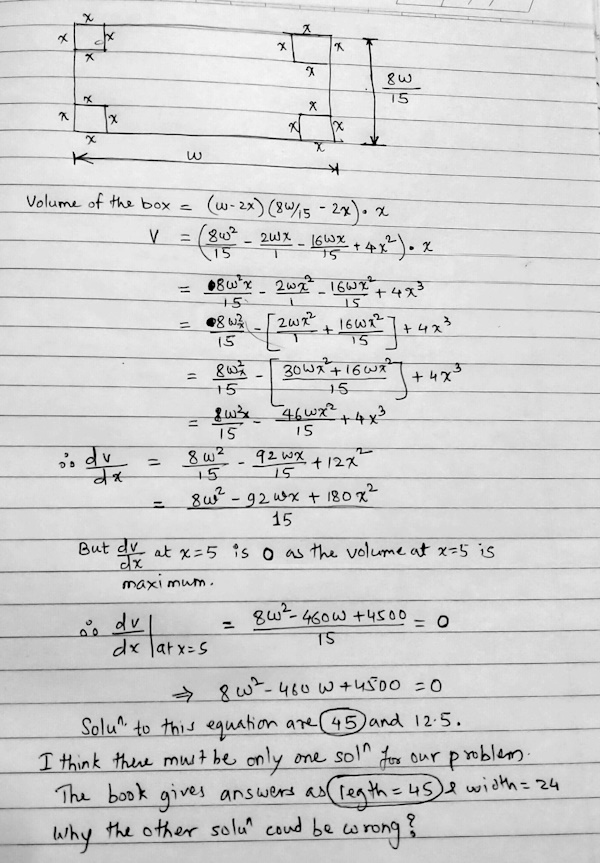Here is an interesting question we got recently, that turns a common maximization problem (the open-top box) inside-out. What do you do when you’re given the answer and have to find the problem? We’ll hit a couple snags along the way that provide useful lessons in problem-solving.
Prologue: how to handle ratios
Rahul asked us this in late August:
I was solving a calculus question about maxima minima.
There I encountered with a seemingly simple problem.
I was given that sides of a rectangle are in ratio 8:15.
I assumed that let the length of the rectangle be x and its width be y.
So y/x = 8/15, so y will be 8x/15. It was to make some equation in one variable.
Am I right in assuming in this way?
Or is it that I have to assume length as 15k and width as 8k, for some k?
After this answer, I would like to ask further question.
Thank you.
Regards,
Rahul.
The first approach, representing the lengths of the sides by two variables and relating them via the ratio, is common for min/max problems; the second, defining the proportional quantities as multiples of a common factor, is common for ratio problems (as a way to avoid fractions).
I answered:
Hi, Rahul.
Both approaches are good. The context might lead me to prefer one over the other, but both would still work.
I might most naturally tend to use his first method; but because methods taught in different cultures may be better than mine (especially for students used to those methods), I didn’t want to bias him! (As it turned out, I used his second approach!)
The problem: An open box
Rahul replied with the details. First, here is the problem:
Notice how this problem is different from the usual maximization problem. Normally, we would be given the actual dimensions of the paper, and asked to find the sizes of the squares at the corners. Here we are told the answer (the size of those squares, which will each have an area of 25 square units, and therefore a side of 5 units), and asked to find the paper size. This makes it a little tricky.
Here is a typical problem, from the book some of my students use:
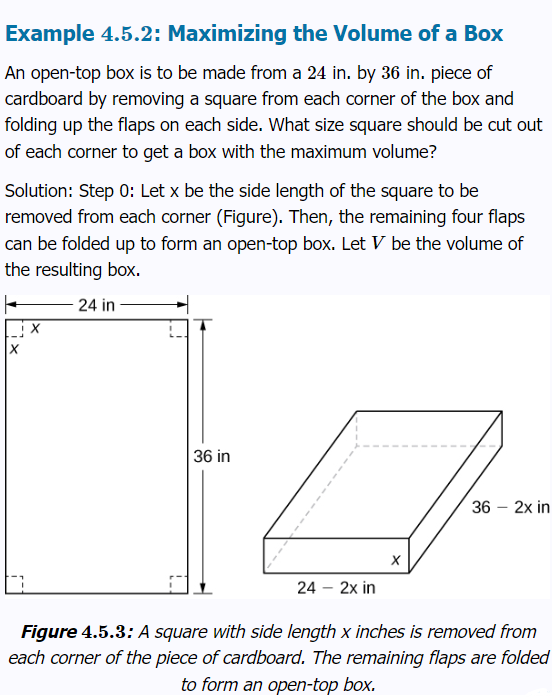
An incorrect solution
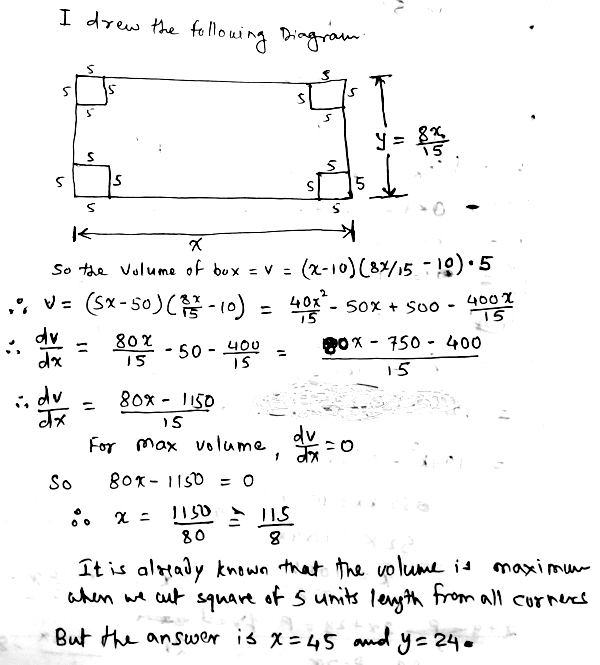
Now, here is Rahul’s work, using his first approach:
Unfortunately, by differentiating with respect to x, he has actually found the dimensions (14.375 by 7.667) at which the volume will be “minimized” (4.375 by -2.333 by 5 = -51.04167 cubic units). That isn’t even a box! In order to make an actual box with the 5-unit squares, x has to be more than 18.75.
I answered, focusing on the most important error:
You’re misinterpreting the problem.
It says,
A rectangular sheet of paper of fixed perimeter with the sides having their length in the ratio 8:15 [is] converted into an open rectangular box by folding after removing the squares of equal area from all corners. If the total area of the removed squares is 100, the resulting box has maximum volume. Find the [dimensions] of the rectangular sheet of paper.
It’s a little awkward the way it’s worded, but what they are saying is that, for a fixed sheet of paper (your x not being allowed to vary), we obtain the largest volume for the box (over all possible sizes of the squares we cut out) when we make those removed squares have a total area of 100. That is, we vary your s, not your x, and find that s = 5 gives the maximum volume.
It happens that I used your approach using dimensions 8k by 15k in my work to avoid fractions, but your way should work if you take dV/ds rather than dV/dx. I found the final steps of my work interesting; there are probably several different ways to do it.
In fact, I had misread his picture, because I expected the size of the squares to be a variable, so I saw all those “5’s” on the squares as “s”. (If I’d read everything, and not stopped at the picture, I would have seen that they were treated as 5!)
What I should have said is, “If you replace 5 with a variable (perhaps s for side), and differentiate with respect to that, then you will be going in the right direction.”
Rahul responded:
Thanks for your reply.
“I am not allowed to vary my x“, was most important thing to know.
Actually, in the diagram as well as in calculation I have used the box height (the length of the square i.e.5 units).
So the volume expression I had written is,
(x-10)*((8x/15)-10)*5. Which is Length * Width * Height.
I have not used the letter s.
So can I use letter s instead of actual value 5 units, and THE LENGTH AS x AND THE WIDTH AS (8x/15).
Using the actual value s = 5 after taking the derivative and equaling it to 0, will that give me the required value of x directly?
Yes, that should work.
I replied:
Ah! I misread that (in fact, that’s why I avoid using the letter s as a variable!), and failed to look closely at your work to see what you actually did, knowing that you had missed the basic idea.
I myself used x for the size of the squares, and took the width and length as 8k and 15k. You might instead use W and 8W/15.
After solving for “s” to obtain the maximum in terms of “x”, you can then set “s” to 5 and solve for “x”, to find the dimensions for which the maximum is obtained when the squares have side 5.
There are several other ways I can imagine doing this.
An almost-complete solution
Rahul replied with a corrected solution, and a new difficulty:
Thanks for the reply.
After all the suggestions I worked on the problem again.
Please find attached file for my work.
Again there is good and bad news that only one of my solutions matched the solution from the book.
In fact the book gives only one solution.
The work is very well done. But what can eliminate the extra solution?
Eliminating the extra solution
I had an answer ready:
At the end of my initial answer, I said,
I found the final steps of my work interesting; there are probably several different ways to do it.
You’ve discovered what I was hinting at! I (briefly) struggled with essentially the same issue, and considered mentioning it more explicitly; but I decided you might use a method that would avoid it, so I left it for discussion later (now).
Did you observe that this is a cubic equation, which will typically have both a maximum and a minimum? Those are what you found!
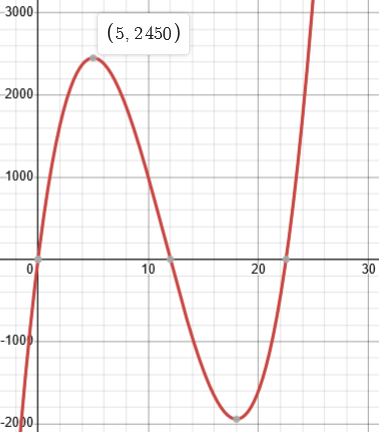
Here is what the function of x looks like when w = 45:
The volume has a maximum at x = 5. This is the solution.
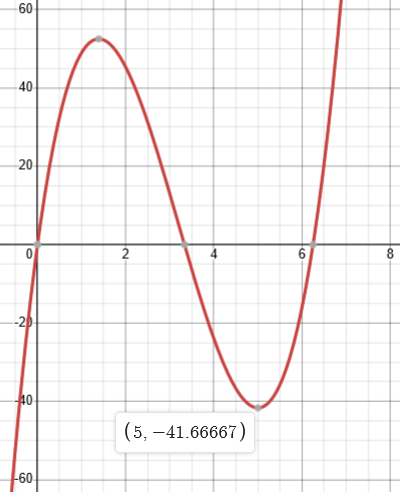
And here is what it looks like when w = 12.5:
Here it is the minimum that occurs at x=5; moreover, the volume is negative!
So how do we decide which to discard?
To eliminate the latter as a solution without graphing, you could check whether it is a maximum, e.g. by the second derivative test, or just check the volume, find that it is negative, and eliminate it because x is not in the domain.
In particular, x can’t be greater than half the width, which for your variables is 8/15 w; for w = 12.5, this is 6 2/3, so x can’t be more than 3 1/3. That’s why this solution must be rejected.
There are a few nice lessons here, aren’t there?
Alternatively, if you just took each of the two solutions and state the full answer (both dimensions), you will find that for \(w=45\), \(\frac{8}{15}w=24\), while for \(w=12.5\), \(\frac{8}{15}w=6\frac{2}{3}\), which is too small to allow for cutting out two 5-unit squares. This is probably the easiest way.
Finishing the work, two ways
Rahul replied:
Yes there are few nice lessons to learn.
Thank you very much.
Please see attached file for my final work after this beautiful workout.
Well done. He could also have used the first-derivative test.
I closed:
Excellent. I hadn’t tried this approach because the negative volume approach is easier; but this is satisfying!
If you’re interested, here’s how I solved it using the “15k by 8k” approach:
This method makes sense not only because it avoids fractions (which is why we might do it in a problem about ratios), but also because the dimensions are fixed, so that k will be a constant. I didn’t want to call the (fixed) sides x and y!
We start with a piece of paper \(15k\times8k\), and cut out four squares with side \(x\), leaving the base of the box with dimensions \(15k-2x\) by \(8k-2x\). The volume of the resulting box is $$V=x(15k-2x)(8k-2x)=4x^3-46kx^2+120k^2x$$
Differentiating this, and setting the derivative to zero, we get $$12x^2-92kx+120k^2=0\\4(3x^2-23kx+30k^2)=0\\4(3x-5k)(x-6k)=0$$ so we get two solutions, \(x=\frac{5}{3}k\) and \(x=6k\). For a cubic with positive leading coefficient, the maximum will be the leftmost critical point, so the solution is \(x=\frac{5}{3}k\); and since we are told that this is 5, we know that \(5=\frac{5}{3}k\) and \(k=\frac{3}{5}\cdot5=3\).
Therefore, the dimensions of the paper are \(15\cdot3=45\) by \(8\cdot3=24\).
An additional difference is that whereas Rahul set x to 5 before setting the derivative to 0, I did the latter first, completing the work of maximizing before returning to the givens of the problem. His way may have saved a little work. Doing that, the end of my work might look like this:
Replacing x with 5 in $$4(3x-5k)(x-6k)=0$$ we get $$4(15-5k)(5-6k)=0$$ so we get two solutions, \(k=3\) and \(k=\frac{5}{6}\). Also, taking \(x=5\) in the volume formula, we have $$V=4x^3-46kx^2+120k^2x=500-1150k+600k^2$$ Our two solutions yield volumes of $$V=500-1150(3)+600(3)^2=2450$$ and $$V=500-1150\left(\frac{5}{6}\right)+600\left(\frac{5}{6}\right)^2=-62.5$$ The former must be the maximum, so the dimensions are \(15\cdot3=45\) by \(8\cdot3=24\).