A recent question dealt with how to write the general solution to a trigonometric equation. I want to combine that with an older question that will set the stage for the issue. This topic was touched on in Trigonometric Equations: An Overview.
Finding all solutions of a cotangent equation
We’ll start with this question from June 2023:
I have solved the problem using the suggested steps given by the book. However, for this particular question I only arrived at one of the two answers. The other one I could not arrive at is 5.7 Rad. What have I done wrong or what have I missed from the book?
Thanks
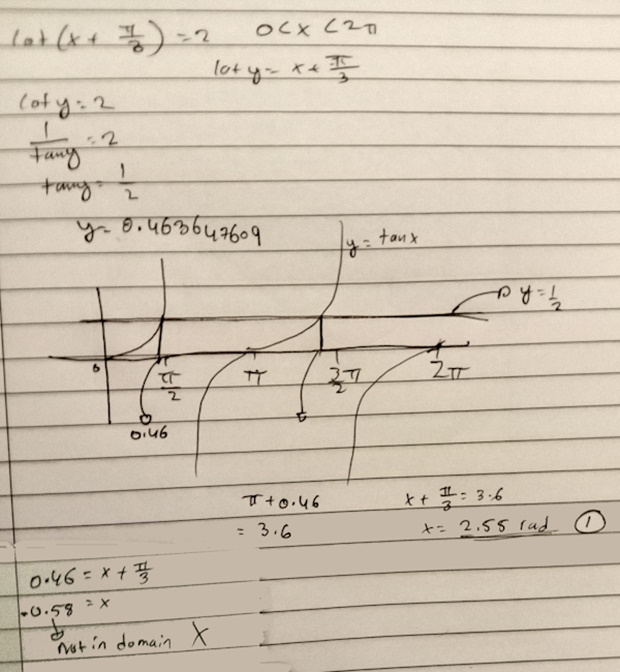
The problem Jamie is trying to solve is $$\cot\left(x+\frac{\pi}{3}\right)=2,$$ looking for all values of x between 0 and \(2\pi\). He started by making a substitution of \(y=x+\frac{\pi}{3}\), so that the equation becomes \(\cot\left(y\right)=2\). Taking the reciprocal of both sides, this becomes \(\tan\left(y\right)=\frac{1}{2}\). One solution of this is \(y=\tan^{-1}\left(\frac{1}{2}\right)\approx0.4636\). Reversing the substitution, he gets \(x+\frac{\pi}{3}\approx0.4636\), so that \(x\approx0.4636-\frac{\pi}{3}\approx-0.5835\). This is rejected because it is not in the required interval.
A second solution is found by adding π to the first solution, obtaining \(y=0.4636+\pi\approx3.6052\), so that \(x\approx3.6052-\frac{\pi}{3}\approx2.5580\). But there is supposed to be a third solution, and the book evidently doesn’t say how to find it.
An example
Jamie had included images of several example problems; here is the one closest to the problem he is solving:
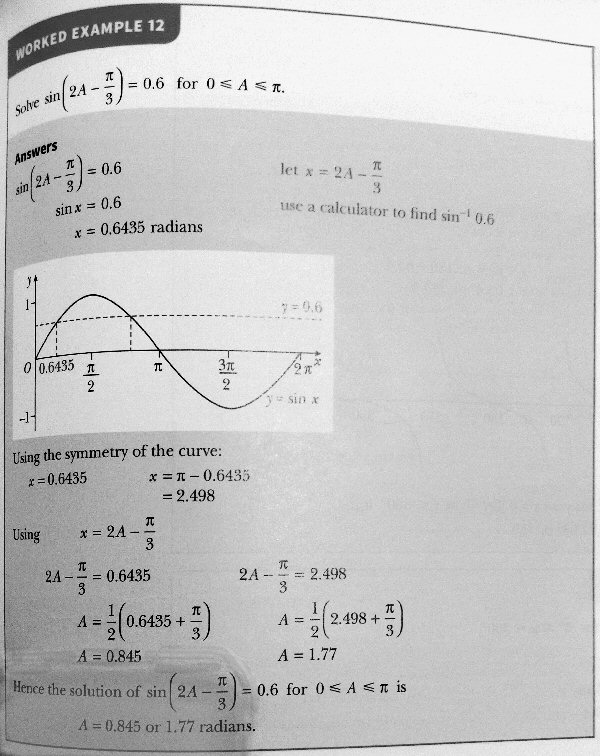
This example has the added complication that the variable is doubled; the method shown suggests they have not yet learned all that we’ll be discussing (about the general solution). They make a substitution like Jamie’s, letting \(x=2A-\frac{\pi}{3}\), and then draw the graph \(\sin(x)\) from 0 to \(2\pi\) without giving a reason for those limits. Possibly it is because A has to be between 0 and \(\pi\), so 2A would be between 0 and \(2\pi\). But if \(0\le A<\pi\), then \(2(0)-\frac{\pi}{3}\le x=2A-\frac{\pi}{3}<2\pi-\frac{\pi}{3}\), i.e. \(-\frac{\pi}{3}\le x<\frac{5\pi}{3}\). What they graphed is good enough for their problem, but our problem will need a little more attention.
They find each solution for x in the interval they graphed, and then back-substitute to find the corresponding values for A.
Many more solutions
Doctor Rick answered,
Hi, Jamie.
Thanks for showing your work. I see that you are solving the equation
cot(x + π/3) = 2
Letting y = x + π/3, you find that one solution of cot y = 2 is y = tan-1(0.5) = 0.4636. Adding π radians (the period of tan y) to that solution, you obtained a second solution, y = 3.6052. You then found the value of x corresponding to each of these values of y:
x = y – π/3 = -0.5825 or 2.558
Only the second of these is in the domain, 0 ≤ x < 2π.
This work follows the example, in making a substitution; but the example didn’t say anything about how to decide how much of the graph to think about, and where to stop. That will be the issue.
Do you think that these are the only two solutions for tan x = 1/2? No, there is an infinite number of solutions — all numbers of the form 0.4636 + kπ, where k is an integer. This is the nature of periodic functions. You have only tried, in effect, k = 0 and 1.
In the example, the first two solutions were tried, and both gave values of x in the specified domain; no more turned out to be needed. This problem is different because we need to look a little further, as we’ll see.
I notice that you only graphed the tangent function for 0 ≤ y < 2π. The solution x is restricted to this interval, but your intermediate variable y is not restricted to this interval! You need to consider all solutions for y, and determine which of these correspond to values of x that are in the given interval. You found that y = 0.4636 corresponds to an x that is too low; keep adding π to y until you find an x that is too high, and then you can be sure you found all solutions.
Explaining the general solution
Jamie asked about Doctor Rick’s work:
How did you derive your answer, 0.4636 + kπ, for better understanding?
Doctor Rick responded:
I suppose you have not yet seen how to write an infinite solution set for a trigonometric equation. In that case, here is a preview of coming attractions!
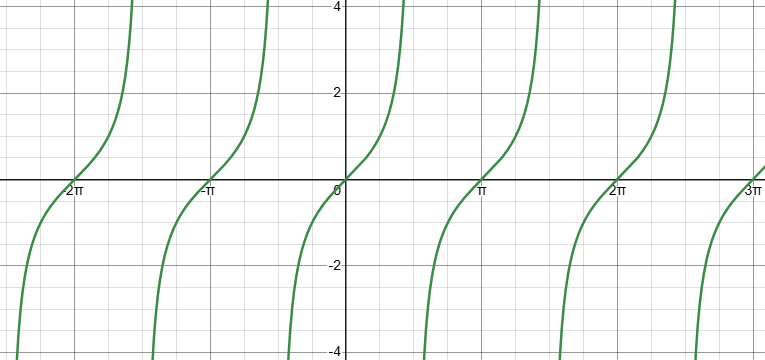
You drew a graph of y = tan x, but only for x between 0 and 2π, just enough to see two periods of the graph. The tangent function, being a periodic function, actually goes on repeating itself forever, like this:
Don’t think of it as stopping anywhere!
The identity tan(x + π) = tan x, which says that the tangent function has period π, implies that if you have one value of x such that tan x = 1/2 (for instance) — let’s call it “a” — then you can add π to that value to get another solution of the equation. But we don’t need to stop there: we can add π to that second value and get a third solution. Adding π to any solution gives us another solution. Thus if “a” is a solution, then all of these are solutions too: a + π, (a + π) + π = a + 2π, (a + 2π) + π = a + 3π, and on and on. In fact, a – π is also a solution, since by the same identity, 1/2 = tan(a) = tan((a – π) + π) = tan(a – π). Thus any one solution gives us an infinite set of solutions:
…, a – 3π, a – 2π, a – π, a, a + π, a + 2π, a + 3π, …
All of these solutions are of the form
a + kπ, where k is some integer.
For example, if we let k = 0, then we get a + kπ = a + 0π = a. If we let k = 3, then we get a + kπ = a + 3π. If we let k = -2, then we get a + kπ = a + (–2)π = a – 2π. Those are all in the list above.
If we add in a line showing where the tangent is equal to 1/2, we see more than just the two places Jamie found (in blue and red); we need to include at least the next one (in purple):
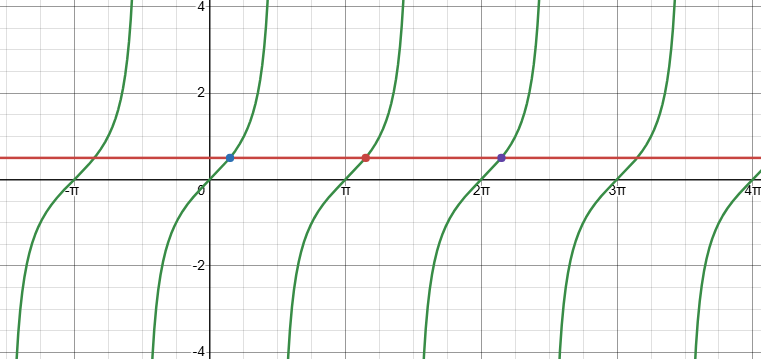
This additional solution, 6.7468, also needs to be considered as a value for y. We’ll see later how to decide what to include.
As I wrote before, the full set of solutions of the equation tan x = 1/2 is
all numbers of the form 0.4636 + kπ where k is an integer.
We have a formal way of writing sets in which what I just wrote looks like this:
{0.4636 + kπ | k ∈ ℤ}
But that’s farther ahead of where you are, probably.
The same applies to other trig functions, with different periods:
The sine and cosine functions have period 2π; that is, we have the identity sin (x + 2π) = sin x, and similarly for cos x. Therefore, if sin a = b then sin(a + 2π) = b, and a, a + 2π, a + 4π, etc., are all solutions of the equation sin x = b. In other words, a + 2πk where k is any integer, is a solution.
Is this enough for you to go ahead?
Jamie wrote back,
I have understood this and have solved the questions. Thank you!
Deciding which solutions to use
Let’s take this a little farther, in two directions: First, how do we actually decide when to stop (that is, when you have all the solutions in an interval); and, second, what can Jamie do without this idea of a general solution? (That is, what should the book have said about their own work?)
Having found the general solution for the substituted equation, \(y=0.4636+k\pi\), we then need to find the general solution for the original equation, by reversing the substitution: $$x=y-\frac{\pi}{3}\approx0.4636-\frac{\pi}{3}+k\pi\approx-0.5835+k\pi$$ Now we can just plug in values for k, seeing which are in the interval \([0,2\pi)=[0.6.2832)\). For \(k=0,1,2,3\) we find \(x=-0.5835,2.5580,5.6996,8.8412\); the middle two are valid, but the others are outside the interval. The two solutions, to the nearest hundredth, are therefore 2.56 and 5.70.
Alternatively, we could solve the inequality \(0\le-0.5835+k\pi<2\pi\) for k to determine which values of k to use; we find that $$0.5835\le k\pi<2\pi+0.5835\approx6.8667,$$ and then $$0.1857<\frac{0.5835}{\pi}\le k<\frac{6.8667}{\pi}=2.1857,$$ so that the only integer values we need for k are 1 and 2, giving the same two answers without having to calculate others.
Solving without a general solution
I mentioned, in discussing the example, at what they omitted in explaining their method: The possible values of the new variable (our y, their x) should be taken into account when finding values for that variable. Jamie’s graph, like theirs, didn’t go far enough to the right to handle all needed solutions.
While working in terms of y, we can find all the solutions within the appropriate interval for y. The interval \(0\le x=y-\frac{\pi}{3}<2\pi\) becomes \(1.0472=\frac{\pi}{3}\le y<\frac{7\pi}{3}=7.3304\), so after finding one solution at \(y=\tan^{-1}\left(\frac{1}{2}\right)\approx0.4636\), and seeing that it is too small, we add π once, making \(0.4636+3.1416=3.6052\), and adding π again takes us to \(3.6052+3.1416=6.7468\), which is still in range; but adding yet again would make it too large.
Now we have two values for y, 3.6052 and 6.7468. These yield solutions \(x=3.6052-\frac{\pi}{3}=2.5580\) and \(x=6.7468-\frac{\pi}{3}=5.6996\).
Alternatively, again, we could just recognize that because y is just x, shifted, solutions for x still differ by π. So after finding the first solution, \(-0.5835\), we can just add π twice to get the required solutions. If our substitution had involved a multiplication, this approach would be a little more involved.
Write all solutions as a single expression?
This September we got this question about a general solution:
I am able to find particular solutions in an interval.
I am able to find different general formula for different solutions.
I am not able to combine the two in one form as a solution.
Request you to help.
Regards,
Rahul.
The problem is to solve \(\sin(\theta)=\sin(\alpha)\) for the variable \(\theta\), given a constant \(\alpha\). We discussed a very similar problem (from a very different perspective) at the end of More On Mixing Trig Functions.
Rahul has two general solutions, \(\theta=\alpha\pm2n\pi\) and \(\theta=\pi-\alpha\pm2n\pi\). But the book’s answer is a single expression, \(\theta=n\pi+(-1)^n\alpha\). Is his own answer correct? How could he get theirs?
I answered:
Hi, Rahul.
First, I want to point out that not all solution sets can be, or need to be, written as a single expression. Often it is better to express it as the union of two simple lists, or something like that, rather than as a single complicated expression. If the solution to an equation were, say, x = π/3 + 2nπ or x = π/4 + 3nπ, I would probably just leave it at that.
Readability is often more important than neatness.
Also, if the answer in a book is given as nπ + (-1)nα, you don’t have to give your answer in the same form. Your answer, α ± 2nπ or (π – α) ± 2nπ, is perfectly acceptable. (I would, however, write it as α + 2nπ or (π – α) + 2nπ, where n is any integer, because the plus-or-minus is not needed; n is not necessarily positive.) If I were unsure of my answer because it differs from the book’s, I might list the first several solutions as implied by each answer, and make sure they agree even though they are written in different forms.
This is easier for a numerical problem like our first one above (if it had asked for the general solution); but here we can list like this:
$$\{n\pi+(-1)^n\alpha\;|\;n=0,1,2,3,4,5,\dots\}=\{\alpha,\pi-\alpha,2\pi+\alpha,3\pi-\alpha,4\pi+\alpha,5\pi-\alpha,\dots\}$$
$$\{\alpha+2n\pi\;|\;n=0,1,2,\dots\}=\{\alpha,2\pi+\alpha,4\pi+\alpha,\dots\}\\\{(\pi-\alpha)+2n\pi\;|\;n=0,1,2,\dots\}=\{\pi-\alpha,3\pi-\alpha,5\pi-\alpha,\dots\}$$
These combine to give the same solutions.
How to rewrite it
But we can change your answer to the book’s form. with a little extra effort. Here is one way:
One set of solutions is α + 2kπ, and the other is (π – α) + 2kπ = (2k + 1)π – α. We can rewrite these both as
α + nπ for any even integer n
-α + nπ for any odd integer n
since any even integer can be written as 2k, and any odd integer can be written as 2k+1.
And since (-1)n = +1 for any even n and -1 for any odd n, we can combine the two cases as
(-1)n α + nπ for any integer n
Does that help?
What we’re doing here is simplifying each of the two solutions in a way that makes them look more similar.
Rahul replied:
Thank you very much for the help.
Yes, I now totally understand how we can change my answer to the books form.
In this single form all the possible solutions can be gotten because n ∈ Z.
Regards,
Rahul.
Another way to see it
A month later, Rahul wrote again, with second thoughts about the same question:
x = nπ + ((-1)^n)y, where n is any integer is a general solution for sin x = sin y.
It is obtained from following 2 solutions,
x = (2n+1)π – y, and x = nπ + y.
I can check for any n and find that it satisfies.
But does not satisfy me.
One approach was writing the solutions as,
x = (2n+1)π + ((-1^(2n+1)) y and
x = nπ + ((-1)^n) y
and then saying that, 2n+1 and n are same.
It still does not satisfy me.
Is there any other trick that could be satisfying.
I hope that the question makes a sense.
Thanks in advance.
Regards,
Rahul.
He didn’t follow up on this when we asked what about my explanation is not satisfying. But perhaps we can improve his attempt (which of course is not valid as written because \(n\) and \(2n+1\) are not in fact the same).
Here is what we can do:
- His first solution, \(x=(2n+1)\pi-y\), can be rewritten as \(x=(2n+1)\pi+(-1)^{2n+1}y\), since \((-1)^{2n+1}=-1\), being an odd power of \(-1\).
- His second solution, \(x=n\pi+y\), applies only when n is even. But if we replace n with 2n, forcing it to be even, then it can be rewritten as \(x=(2n)\pi+(-1)^{2n}y\), since \((-1)^{2n}=1\), being an even power of \(-1\).
So we have that for any n, \(x=(2n+1)\pi+(-1)^{2n+1}y\) and \(x=(2n)\pi+(-1)^{2n}y\). But any k can be written as either \(2n\) or \(2n+1\), and these equations both become \(x=k\pi+(-1)^ky\). So that is our general solution!