Let’s look at three similar questions we’ve received about Least Common Multiples, Greatest Common Factors, and so on, starting with a recent question and going back in time. We’ll see a bad question, a good question, and an interesting challenge.
Given HCF, LCM, and one number, find other number
Recall, first, that the GCF (Greatest Common Factor) of a set of numbers is also called the GCD (Greatest Common Divisor), or HCF (Highest Common Factor). The LCM is the Least Common Multiple.
For example, given the numbers 12 and 30, their GCF is 6, because \(12=6\times2\) and \(30=6\times5\), and nothing larger is a divisor (factor) of both. Their LCM is 60, because \(12\times5=60\) and \(30\times2=60\), and nothing smaller is a multiple of both.
These are discussed in
Three Ways to Find the Greatest Common Factor
Many Ways to Find the Least Common Multiple
(The three questions we’ll look at are from India, Singapore, and Bangladesh; all used the term HCF. We’ll sometimes use their terms, and sometimes GCD or GCF.)
We’ll start with this question that came from Manish, a teacher, in March:
The HCF and LCM of two numbers are 33 and 264 respectively. When the first number is completely divided by 2, the quotient is 33. Find the other number.
My work:
Let the first number be a and the other number is b.
Therefore, LCM(a, b) = 264 and HCF(a, b) = 33.
Since, the first number is completely divided by 2, the quotient is 33,
a = 2 × 33 = 66.
As we know a × b = LCM(a, b) × HCF(a, b).
Then
b = [LCM(a, b) × HCF(a, b)] ÷ a
b = (264 × 33) ÷ 66 = 132
But HCF of 132 and 33 is not 33 instead its 66
132 = 33 × 2 × 2
66 = 33 × 2
HCF = 33 × 2 = 66
Please clarify Sir
Thank you
The fact that \(LCM(a,b)\cdot HCF(a,b)=ab\) was discussed here.
The work is good, but it looks like the answer, 132, doesn’t work. What is wrong?
Doctor Rick answered:
I see no conclusion to draw other than that the problem is faulty: there is no such other number.
The expression, “When the first number is completely divided by 2, the quotient is 33,” is unfamiliar to me, but I think it must mean that the result of dividing a by 2 is 33 with no remainder, so that a = 2·33 = 66. And you are correct, this leads to the conclusion that b = 132, but HCF(66, 132) = 66, not 33.
My own first impression was that the phrase “completely divided by 2″ might be intended to mean “is divided by 2 until no factors of 2 remain”, or equivalently “is divided by the highest possible power of 2”. It is definitely not part of my own dialect. I searched for uses of the phrase, and found that it sometimes (mostly in India?) is taken to mean “divisible by 2″; but the grammar here – being used as a verb, not an adjective, resulting in a quotient – makes that impossible.
The only place I found the phrase in a similar context is this . very . problem, which is solved identically in many places, with Manish’s answer (even a couple of videos), but none of these check, as Manish did, to see that it doesn’t work!
(I also found a similar problem in which our 264 was replaced by 198; that one works.)
We can check the answer a different way:
We can list all the multiples of 33 = 3·11 that are factors of 264 = 23·3·11:
3·11, 2·3·11, 22·3·11, 23·3·11
All possible pairs (a, b) satisfying the conditions HCF(a, b) = 33, LCM(a, b) = 264 must be in this list; but unless 33 is one of the pair, HCF(a, b) will be greater than 33.
This list was made by observing that all such numbers must be 33 times some part of the remaining factor, \(2^3=8\), so they are 33, times 1, 2, 4, or 8. But unless 33 itself is one of the numbers, the HCF will not be 33.
My guess is that the writer of the problem used the rule you used without realizing that the check is needed. It is true that
If HCF(a, b) = p and LCM(a, b) = q, then pq = ab.
However, this is not an “if and only if”. The converse is not true:
If HCF(a, b) = p and pq = ab, then q = LCM(a, b). [FALSE]
Though q will be a common multiple of a and b, it is not necessarily the least common multiple. Thus, given a, p, and q, after we find b, we need to check whether HCF(a, b) really equals q.
It’s amazing that so many people have shown solutions to this problem, and none of them (that I found) thought to check it!
Thinking visually about factors
The fact that \(LCM(a,b)\cdot HCF(a,b)=ab\) was illustrated here with this Venn diagram:
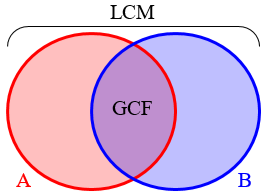
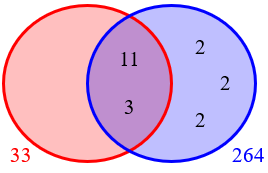
Each number (A and B) is the product of all the prime factors we’ll put into its circle; the LCM is the product of all of them, and the GCF is the product of just those in the overlap. If we multiply A and B together, we are multiplying all factors in the LCM, and those in the GCF a second time, which explains the formula.
In our case, \(GCF=33=3\cdot11\) and \(LCM=264=2^3\cdot3\cdot11\), so we can place 3 and 11 in the middle, and have three 2’s left to place. We are told that A is 2 times the GCF, so we have to do this:
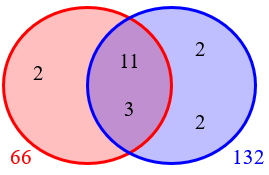
But then the two numbers have another common prime factor, 2, so the GCF is really 66, not 33 as required:
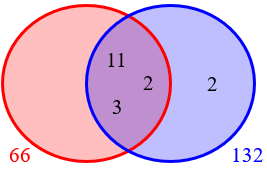
So we don’t have the right GCF or LCM.
On the other hand, what if we weren’t told anything about either number? Once we have the GCF filled in, we have three 2’s left over from the LCM that have to be put somewhere:
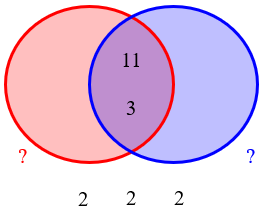
They all have to go on one side or the other, since if there were some on each side, we would have an extra common factor, and the GCF would be wrong. So the only pair of numbers that will work are these:
So it turns out that the only version of the problem that makes sense is if we take “completely divided by 2” to mean, as I had originally surmised, “divided by the largest possible power of 2”. I doubt that’s what was really intended, though; I’ve found no evidence of it being used that way. (Also, that requirement turns out to add nothing to the problem.)
This led me to check whether we have answered any similar problems in the past, and I found that we did; these will add some useful ideas to the discussion.
Given LCM, HCF, and bound, find both numbers
We got a valid question of this type in July 2021:
I wrote the prime factorisations below but I don’t know what to do after.
Find two numbers, both smaller than 100, that have a lowest common multiple of 450 and a highest common factor of 15.
LCM = 450 = 2×32×52
HCF = 15 = 3×5
This is similar to my modified version of the first problem, where we are given only the LCM and HCF; we can guess that the restriction on the size of the numbers prevents there being too many solutions.
Doctor Fenton answered:
Hi Louis,
You are off to a good start, by finding the prime factorizations of the GCD and LCM. It seems you know that the GCD must contain all the primes which divide both numbers, and the LCM must contain all the primes which divide either number. In addition, if a prime divides both numbers but occurs to different powers in the prime factorizations, the GCD will contain that prime to the smallest power which occurs in both numbers, and the LCM will contain that prime to the largest power which occurs in either number.
For example, if the prime 3 occurs in one number to the power p, and in the other number to the power q, and if p < q, then the GCD will contain the factor 3p and the LCM will contain the factor 3q.
Here is a typical example:
\(\;\;\;\;180=2^2\times{\color{Red}{3^2}}\times5^1\\\;\;\;\;\;54=2^1\times{\color{Green}{3^3}}\times5^0\\GCD=2^1\times{\color{Red}{3^2}}\times5^0=18\\LCM=2^2\times{\color{Green}{3^3}}\times5^1=540\)
Any factor of 180 must have no more than 2 3’s in its factorization. Any multiple of 54 must have at least 3 3’s in its factorization. So we use the smaller power of 3 in the GCD, and the larger power of 3 in the LCM.
For our problem, we have to think backward:
For example, in your problem, the GCD prime factorization contains only one factor of 3, while the LCM prime factorization contains 32. So one number must be divisible by 3 (but not by 9), and the other must be divisible by 9.
One such pair of numbers with GCD 15 and LCM of 450 is n = 3×5 = 15 and m=2×32×52 = 225, but that doesn’t solve your problem because both numbers must be less than 100. Can you find find a way to distribute the prime factors to make both numbers less than 100?
Here, he put all the extra factors in B:
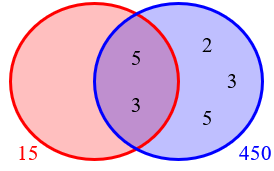
But they don’t have to be all together. Our task is to distribute (place) these factors such that neither number will be greater than 100.
Louis wanted more help:
Can you teach me how to distribute? The first time I tried this question my answer was 450 and 15 ;-; I need more help on the concept of distribution
Ultimately, it will come down to trying things. It is likely that Louis expects to be able to find the answer by some routine method, rather than trial and error (guess and check); but the latter is perfectly valid math!
Doctor Fenton replied:
Look at it this way: you want two numbers whose LCM is 450 and whose GCD is 15.
(1) that means that both numbers must be divisible by 15, so they have at least one 3 and one 5 in their prime factorizations.
(2) To make the LCM 450, one number must be divisible by 9 and one number must be divisible by 25. Since the question asks you to find two numbers, both less than 100, it can’t be the same number which is divisible by 9 and by 25: if it were, then that number would be a multiple of 9×25=225, which is larger than 100.
So one number must be 3×52, perhaps multiplied by another prime, and the other number must be 32×5, perhaps multiplied by another prime. The LCM also has a factor of 2, so one of the numbers must be divisible by 2. Which one could it be? Could it be either, or must it be one of the two above?
Here is our second failed attempt, making B divisible by both 9 and 25, but not by 2 as before:
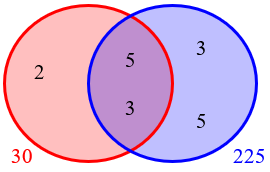
That doesn’t work; neither would this, with A divisible by 9, and B by 2:
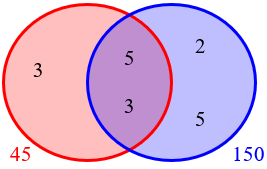
Louis made another attempt:
For the first number I put 5^2 because 3×5 is 15, and it cannot be 15 as it’s already stated in the question?
One number must be divisible by 15.
One number must be divisible by 9 and one number divisible by 25.
First number = 3×52 ??
Second number = 2×32×5
That works:
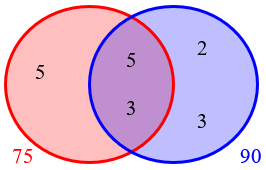
Doctor Fenton agreed:
Your work is correct: 3 × 52 = 75; and 2 × 32 × 5 = 90, so 75 and 90 are the two numbers the problem asks for. Good work!
What we see in this problem is typical: unlike the first example (without the given number), there are multiple possibilities unless we have an extra condition. This problem (unlike our first) was well-designed.
Given a sum and a ratio, find the LCM
Finally, we have a question from March 2021, which has a different feature:
The sum of two positive integers is 2022. The LCM of the numbers is 2018 times of their HCF. What is the LCM of the numbers ?
Hello sir,
I’ve been trying to solve the problem but I don’t know how to do so. I’m stuck at the very beginning and don’t have any clue. So I’m sorry that I wasn’t able to send you any progress of my trying to solve the problem.
Can you please help me catch up?
This time we have only relationships (the sum of the numbers, and the ratio of the LCM and HCF) rather than any specific numbers. So it looks like we’ll be doing algebra rather than just arithmetic. Or maybe not …
Doctor Fenton answered with some general hints at how to start thinking about such a problem at all:
Hi Shuvodip,
One thing you might think about is how to go about finding the HCF and LCM of two numbers. (You can find the HCF with the Euclidean algorithm, but it doesn’t give you the LCM.) If I gave you two numbers and asked you to find their HCF and LCM, how would you go about it? Suppose I would tell you anything you want to know about the two numbers, what would you ask me for that would make finding the HCF and LCM easy?
You might also just pick a couple of numbers, find their HCF and LCM and the relationship between the two, and see what that tells you about the two numbers.
Do either of these give you some hints on how to approach the problem?
The hints are aimed at getting Shuvodip thinking about how the various numbers are related, without being very specific. “What you would want to know” is their factorizations!
Shuvodip didn’t respond; let’s see what we can do, using the various tools we’ve seen..
Using algebra
My first thought is to use algebra, using some ideas we haven’t quite seen yet.
Let’s call the two numbers a and b, and define \(d=GCD(a,b)\) and \(m=LCM(a,b)\). Then we are given that $$a+b=2022\\m=2018d$$ The fact that \(LCM(a,b)\cdot HCF(a,b)=ab\) means that \(ab=md\). So $$a+b=2022\\ab=2018d^2$$ Can we do anything with this? The trouble is, we have two equations in three unknowns, with the additional knowledge that the variables are all integers, so this is a Diophantine problem. I don’t see anything useful yet.
Factoring the big numbers, we have \(2022=2\cdot3\cdot337\) and \(2018=2\cdot 1009\).
Each number is a multiple of the GCD, so we can say \(a=hd\) and \(b=kd\), where h and k have no common factors. Then the LCM is \(m=hkd\). That is, $$LCM=\frac{ab}{GCD}=\frac{hd\cdot kd}{d}=hkd$$
Now our givens become $$hd+kd=2022\\hkd=2018d$$ Simplifying, $$(h+k)d=2022=2\cdot3\cdot337\\hk=2018=2\cdot 1009$$
I’ll suppose that \(a<b\), so that \(h<k\). The second equation tells us that either \(h=2,k=1009\), or \(h=1,k=2018\). The first equation therefore becomes either \(1011d=2022\) (so that \(d=2\)), or \(2019d=2022\) (which can’t work).
So we have our solution: \(h=2,k=1009,d=2\) so \(a=hd=4\) and \(b=kd=2018\). Their sum is 2022, and \(LCM(a,b)\div HCF(a,b)=4036\div2=2018\) as required.
Distributing factors
The simple factoring suggests there’s an easier way, without explicit algebra.
The LCM is the product of the GCD and the extra factors of A and B. (That is, \(m=hkd\).) Since \(m=2018d\). we know that \(hk=2018=2\cdot 1009\), so that, as before, \(h=2,k=1009\), or \(h=1,k=2018\). The former leads to this Venn diagram:
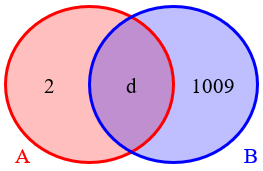
But then \(a+b=2d+1009d=1011d\), and if this is 2022, then the GCD must be \(d=2\):
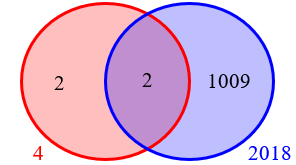
That’s really the same work without dressing it up as algebra!

Pingback: Assertions, Reasons, and Logic – The Math Doctors