Solving Equations with Newton’s Method

Last time we solved some of the equations connected with a segment of a circle using Newton’s Method. Let’s take a closer look at the method – how it works, why it works, and a few caveats.

Introducing numerical approximation

Here is the question, from 2007:

Using Newton's Method to Solve an Implicit Equation

How do you solve the equation sine theta/theta = 0.7031?  The answer given for the value of theta was 80.3 degrees and I cannot seem to see how they did it.  The text just said "solving numerically, the answer is 80.3 degrees."  

Thanks for your help!

We showed how to solve the general form of this equation, \(\displaystyle\frac{\sin(x)}{x}=k\), last time.

Doctor Minter answered:

Hi Vanessa,

Solving equations like these is the basis for an entire branch of mathematics called numerical analysis.  That's why your textbook just says "solving numerically," and leaves it at that.  Usually, numerical analysis methods are taught in a numerical analysis (aka "numerics") course, so your textbook (calculus, perhaps?) does not go into how this type of equation is solved.

The phrase “solving numerically” could also mean “using a calculator that does this”! Graphing calculators and many online sites provide numerical solutions without explaining their methods. Calculus books commonly do teach at least one numerical method, but in other contexts it is not uncommon that the method is not as important as the result.

Let me elaborate on what I mean by "this type" of equation.  This equation is called "implicit."  You cannot isolate the variable on one side of the equal sign in an implicit equation.  From your problem, we have

  sin(t) / t = 0.7031 (where t is used instead of theta)

so

  sin(t) = 0.7031 * t

To invert the sine function, we would have to take the arcsine of both sides.  That would give us t by itself on the left, but an arcsine function of t on the right.  The only way to invert the arcsine function is to take the sine of both sides, and we're back where we started, and no better off.  Thus, we cannot solve this equation for t.  Because you cannot solve for t, this equation is implicit.

Some implicit equations can be solved; for instance, if we had \(\displaystyle\frac{x^2-1}{x}=0.7031\), we could write it as \(x^2-1=0.7031x\), and solve the quadratic equation \(x^2-0.7031x-1=0\) using the quadratic formula. When you can’t do that, it’s time to pull out the numeric tools!

For your information, there are a great many ways to find values of t that solve this equation.  All of them are approximations.  By applying the numerical methods, you can get an approximation that is as accurate as you like (that is, up to as many decimal places as desired), but the result will never be exact.  Of course, there's not much difference in two numbers whose first several decimal places are equal, so at some point, we have to say "That's close enough."

Elsewhere, we’ve shown a number of numerical methods, for example, to find square roots, one of which happens to be what we’ll spend the rest of the time with here. And we’ve looked at numerical methods for calculating trigonometric functions.

Newton’s method

In my opinion (but it's just an opinion), the best way to solve this type of equation is called Newton's Method, after the same Isaac Newton that you hear about often in basic physics.  Other methods that come to mind are the Bisection Method, the Secant Method, and the Fixed Point Algorithm.  However, Newton's Method tends to be superior under the right conditions.  I won't get too far into what the "right conditions" are, but suffice it to say that this problem definitely has all the right conditions to use Newton's Method.

There is some very good information about how Newton's Method works on Wikipedia and Math World at the following links:

  Newton's Method
    http://en.wikipedia.org/wiki/Newton's_method 
    http://mathworld.wolfram.com/NewtonsMethod.html

We discussed several methods, including some of these, in Numerical Approximation Methods: When Algebra Doesn’t Work.

The result of the derivation of Newton's Method is

  t_(n+1) = t_n - f(t_n)/f'(t_n)

where t_(n+1) is your "next" approximation, t_n is your "current" approximation, f is the function that you're working with, and f' is that function's derivative.  That is, f' = df/dt.  The underscores denote subscripts if you're writing it on paper.  Make a special note of this above equation because we'll be using it throughout.

That is, $$t_{n+1}=t_n-\frac{f(t_n)}{f'(t_n)}$$

Let’s see where this formula comes from, since Doctor Minter didn’t do that.

Here is the function we’ll be using below; we’ve chosen a starting value of \(a=1\), and drawn in the tangent there:

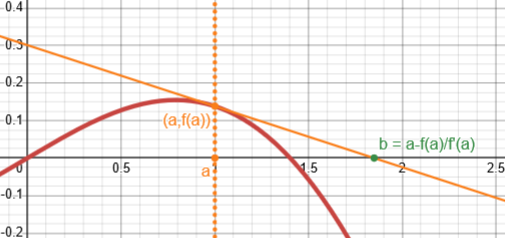
Since the slope of the tangent is \(f'(a)\), the tangent line is \(y=f(a)+f'(a)(x-a)\). Setting this to zero and solving for x to find its x-intercept, we get $$f(a)+f'(a)(x-a)=0\\x-a=-\frac{f(a)}{f'(a)}\\x=a-\frac{f(a)}{f'(a)}$$

We’ve followed the (yellow) tangent line from the point at a to a new point, b. If the function were a straight line, then that would be the solution to \(f(x)=0\). It isn’t; and in fact, this is no closer than our first guess. But we can repeat the process, starting with this new value, \(b=a-\frac{f(a)}{f'(a)}\), as our next guess:

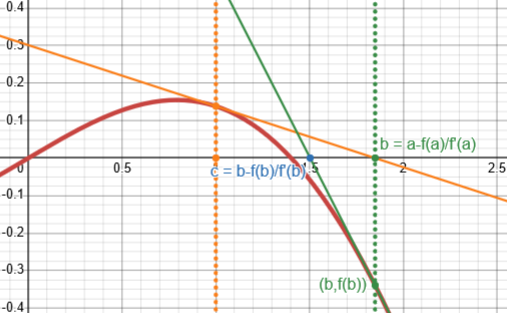
We’ve followed a new (green) tangent line to a new point, c. That’s closer! And we can repeat yet again, using this new value \(c=b-\frac{f(b)}{f'(b)}\):

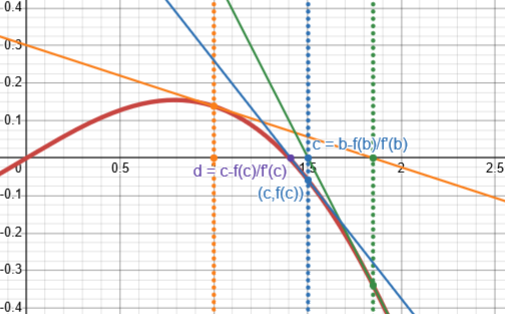
The new value, d, is very close!

That’s a preview of what we’ll be doing below.

Choosing a function

Let's start with the function f in this problem.  What is this function?  We have

  sin(t)/t = 0.7031

How do we get a function out of this?  Newton's Method is also called a "root-finding" method, so we need to transform the above equation into something of the form f(t) = 0.  While it is perfectly legitimate to subtract 0.7031 from both sides to obtain

  sin(t)/t - 0.7031 = 0,

we'll end up having to differentiate this function, so looking ahead, we should use

  sin(t) = 0.7031 t

  sin(t) - 0.7031 t = 0

where the left side is much easier to differentiate.  Thus, we let 

  f(t) = sin(t) - 0.7031 t

and we have our form f(t)=0.

As with many things we’ll be doing here, there is not just one way of doing things when you are approximating!

If we had used the function \(\displaystyle f(t)=\frac{\sin(t)}{t}-0.7031\), its derivative would be \(\displaystyle f'(t)=\frac{t\cos(t)-\sin(t)}{t^2}\), which is a  little harder to work with than what we’ll be doing. But in some cases, it might be worth using a harder derivative if that makes the approximation converge faster. In this case, we’ll find that this choice does in fact work a little better. We’ll be carrying out the work both ways below.

Here are the graphs of both functions, \(\displaystyle f(t)=\sin(t)-0.7031t\) in red and \(\displaystyle f(t)=\frac{\sin(t)}{t}-0.7031\) in green:

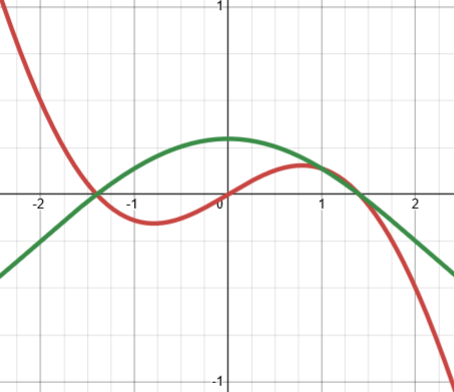
Not surprisingly, they share the same roots, except for 0 (which is not a solution of the original equation).

Making an initial guess

Now, we need our t_n.  Since we have t_n and t_(n+1), the equation for Newton's Method will always have two t's, and their subscripts will be one number apart.  So if we know t_0, we can find t_1, which we can use to find t_2, which we can use to find t_3, and so on.

So all we need is t_0 and we can find the rest by re-using the formula for Newton's Method.  For your information, this type of equation that we can keep reusing to find more values of t_n is called a "recursive relation."

Recursion is more common than you may realize; it is the basis of “lather, rinse, repeat (and repeat, and repeat)”. If we’re doing the right thing, each step will be an improvement.

How do we find t_0 ?  The answer is, "you don't."  That's not to say that we don't NEED a t_0 because we certainly do.  But there's no way to FIND t_0.  What do we do?  Just guess!  That may seem like a strange thing to do in math, but it's actually quite common in numerics and differential equations.

But we shouldn't just shout out some random number.  It's always better to have an "educated guess."  How do we come up with an educated guess?  Just think of a number that you think might come CLOSE to solving

  sin(t)/t = 0.7031

A good way to do so is to rewrite this equation as

  sin(t) = 0.7031 * t

and try to come up with a value of t that makes the two sides equal.  A graph is a very powerful tool in this case.  Graph the function sin(t) and the function 0.7031 * t on the same axes.  The intersection point is the value of t that we're ultimately looking for, because that's the value that solves the implicit equation.

We don’t need to have a graph of our function f, such as those above. As the example suggests, we can just sketch the basic functions involved in our problem. Here is the suggested graph, with \(y=\sin(x)\) in red and \(y=0.7031x\) in green:

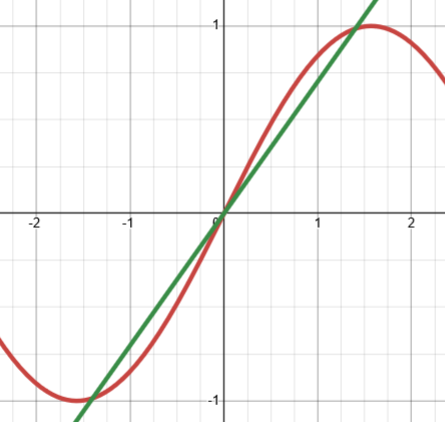
With this accurate graph, we could guess that the answer is about 1.4 radians. But we don’t need to be that accurate; we could just observe from a quick sketch that the intersection will be somewhere near \(\frac{\pi}{2}\approx1.57\), which might suggest trying 1.5. We’ll be keeping it even simpler than that as we proceed.

I want to take a second to tell you that this problem should be solved in RADIANS, and not DEGREES.  Many of the mathematical formulas are designed for use in radians, and not degrees.  Many methods will not work if degrees are used instead of radians, and this method that we're working with here is no exception.  One radian is approximately 57.3 degrees.

If we had tried to check the book’s answer, we might have tried evaluating  $$\frac{\sin(80.3^\circ)}{80.3^\circ}\approx\frac{0.9857}{80.3^\circ}\approx0.012275$$ which is clearly wrong.

To do it correctly (according to what the equation actually means), we have to convert \(80.3^\circ\) to radians (\(80.3\cdot\pi\div180=1.4015\)) and check with that value: $$\frac{\sin(1.4015)}{1.4015}\approx\frac{0.9857}{1.4015}\approx0.7033$$

That’s a little off, presumably due to rounding (we’ll see below that a better approximation is \(80.33^\circ\)).

Thus, why don't we start with t_0 = 1 radian?  Beforehand, we know that the answer is just over 80 degrees, so we expect the answer to be between 1 and 2 radians.  It doesn't matter if t_0 is too high or too low.  It's just a starting point to work with.

If we found that our guess didn’t work, we could just try another guess.

If you read the last post, on circle segments, you may recall that this particular problem is Case 1, where we solved \(\displaystyle f(x)=\frac{\sin(x)}{x}-k\) for any value of k; the instructions there said to start with \(x_0=\sqrt{6-6k}\), which in this case is \(x_0=\sqrt{6-6(0.7031)}\approx1.3347\). We can see from the graphs above that this is quite close.

Making and using the formula

Now, we need to differentiate f(t) because Newton's method involves the function f'(t).  Basic differentiation rules will show that

  f'(t) = cos(t) - 0.7031

Now we have all of the pieces that we need.  We can start with the Newton's Method formula with n=0.  Thus, let t_0 = 1, and let

  f(t_0) = sin(t_0) - 0.7031 t_0 = sin(1) - 0.7031

and

  f'(t_0) = cos(t_0) - 0.7031 = cos(1) - 0.7031

Putting these pieces into the formula gives us

   t_1 = 1 - (sin(1) - 0.7031*1)/(cos(1) - 0.7031)

where the two minus signs (one from the formula, one from the denominator) have canceled.  That's why there's a plus after the 1, when there was a minus before.  Putting this into a calculator or computer shows that t_1 is approximately 1.850.

In editing this, I discovered a sign error in Doctor Minter’s work, which I’ve corrected here and through the rest of the work. (The clue was that the points in the graphs I started with above were “wrong”.)

So our recursive formula is $$t_{n+1}=t_n-\frac{f(t_n)}{f'(t_n)}=t_n-\frac{\sin(t_n)-0.7031t_n}{\cos(t_n)-0.7031}$$

so that, in particular, with \(t_0=1\), $$t_{1}=t_0-\frac{\sin(t_0)-0.7031t_0}{\cos(t_0)-0.7031}=1-\frac{\sin(1)-0.7031(1)}{\cos(1)-0.7031}=1-\frac{0.13837}{-0.16280}=1.84994$$

The next step is to plug the number we just obtained BACK into the formula for Newton's Method, with n=1.  Thus,

   t_2 = 1.850 + (sin(1.850) - 0.7031*1.850)/(cos(1.850) + 0.7031)

Putting this into a calculator, we see that t_2 = 1.503.  Now we plug 1.503 into the formula with n=2 to obtain t_3 = 1.410, plug that into the formula with n=3 to obtain t_4 = 1.402, and so on.

Again, $$t_{2}=t_1-\frac{\sin(t_1)-0.7031t_1}{\cos(t_1)-0.7031}\\=1.84994-\frac{\sin(1.84994)-0.7031(1.84994)}{\cos(1.84994)-0.7031}\\=1.84994-\frac{-0.33940}{-0.97863}=1.50313$$

$$t_{3}=t_2-\frac{\sin(t_2)-0.7031t_2}{\cos(t_2)-0.7031}\\=1.50313-\frac{\sin(1.50313)-0.7031(1.50313)}{\cos(1.50313)-0.7031}\\=1.50313-\frac{-0.05914}{-0.63549}=1.41007$$

$$t_{4}=t_3-\frac{\sin(t_3)-0.7031t_3}{\cos(t_3)-0.7031}\\=1.41007-\frac{\sin(1.41007)-0.7031(1.41007)}{\cos(1.41007)-0.7031}\\=1.41007-\frac{-0.00431}{-0.54306}=1.40213$$

The drawback to these "recursion relations" is that you can't skip ahead.  Note that we needed t_1 to obtain t_2, and t_2 to obtain t_3, and so on.  Nevertheless, recursion relations are powerful tools indeed, as long as you have the beginning terms to get you going.  In this case, that was t_0, which, for obvious reasons, is sometimes called an "initial guess."

If you keep plugging in these numbers, you'll soon notice that with each step, they don't change very much as you keep going.  When you get to t_5, you should notice it is still 1.402, out to the thousandths decimal place.  Of course, t_4 and t_5 aren't EXACTLY equal, but they're very close, and recall that at some point, we have to say, "That's close enough."  

When the answers stop changing by very much, that means that you're very close to the actual value of t that solves the original equation.  Thus, since t_4 and t_5 are so close, let's use t=1.402 as our approximation to the answer.

Let's see if it works:

   sin(1.402)/1.402 = 0.7031

And it does!  Now, we note that 1.402 is approximately 80.33 degrees, using 1.402 * 180 / pi.  So we have arrived at the answer that your textbook gave, which is a very good sign.

Obviously, it’s a lot easier if we let a computer do the work. We can put this formula easily into a spreadsheet (here I’ve displayed 6 decimal places), and we get these results:

step	x	f(x)	f'(x)	delta x
0	1.000000	0.138371	-0.162798
1	1.849957	-0.339417	-0.978649	0.849957
2	1.503134	-0.059142	-0.635489	-0.346823
3	1.410069	-0.004308	-0.543064	-0.093065
4	1.402136	-0.000031	-0.535238	-0.007934
5	1.402078	0.000000	-0.535181	-0.000058
6	1.402078	0.000000	-0.535181	0.000000

So after only 6 iterations, we have 6 decimal places of accuracy.

And if we had started with a better guess, we would have reached the same level of accuracy even sooner. For example, if we had started with the Case 1 initial guess of \(x_0=\sqrt{6-6(0.7031)}\approx1.3347\), we would, in effect, have skipped the first couple steps above.

step	x	f(x)	f'(x)	delta x
0	1.334691	0.033835	-0.469182
1	1.406806	-0.002542	-0.539844	0.072115
2	1.402098	-0.000011	-0.535201	-0.004708
3	1.402078	0.000000	-0.535181	-0.000020
4	1.402078	0.000000	-0.535181	0.000000

Please refer to the links above to see exactly how Newton's Method works, if you're interested.  It's very clever.  Please also note that sometimes Newton's Method DOES NOT WORK, and also that sometimes Newton's Method can be VERY SLOW, in that you may have to repeat the process hundreds or even thousands of times to get a good approximation.  This problem, however, worked very nicely.  Keep in mind that the closer your initial guess is to the right answer, the less times you have to apply the formula to get a good approximation.

Experimenting with the process

Now, recall the other option we had, of solving \(\displaystyle f(t)=\frac{\sin(t)}{t}-0.7031\). Here are the steps to get six decimal places that way, again starting with our very rough guess of 1, but converging a little quicker:

step	x	f(x)	f'(x)	delta x
0	1.000000	0.138371	-0.301169
1	1.459447	-0.022152	-0.390441	0.459447
2	1.402710	-0.000242	-0.381806	-0.056736
3	1.402078	0.000000	-0.381705	-0.000633
4	1.402078	0.000000	-0.381705	0.000000

But if we made a less accurate guess, we could get an entirely different answer for our original work. Here is what happens if we use \(\displaystyle f(t)=\sin(t)-0.7031t\) but start with \(x=0.85\):

step	x	f(x)	f'(x)	delta x
0	0.850000	0.153645	-0.043117
1	4.413465	-4.058761	-0.997592	3.563465
2	0.344907	0.095605	0.238007	-4.068558
3	-0.056783	-0.016828	0.295288	-0.401690
4	0.000207	0.000061	0.296900	0.056990
5	0.000000	0.000000	0.296900	-0.000207
6	0.000000	0.000000	0.296900	0.000000

Graphing the first few steps above, we see that the low slope at the starting point sent the first step wild:

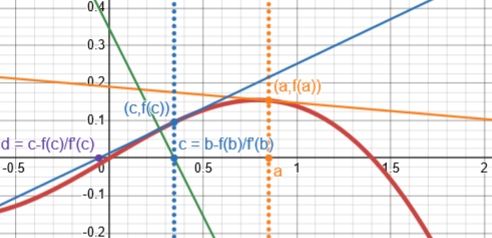
What’s happening here? Let’s zoom out:

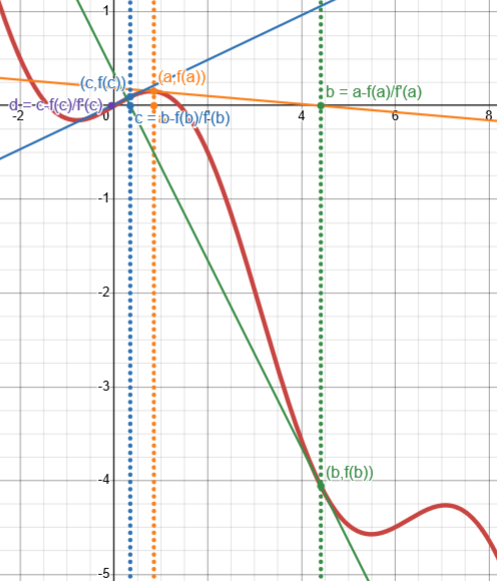
We were very lucky to come back at all near the starting point; but by eventually converging at zero, which is not a solution of the original equation, we totally failed. Another initial guess might lead to the negative root, or perhaps never converge at all.

This illustrates what can go wrong. Next time, we’ll look a little more deeply into that.