Last week we examined three probability problems that had problems. Looking further back, I find that Jonathan, who asked the first of those questions, asked a group of questions about rolling multiple dice in 2022. They provide some additional lessons about easy mistakes to make.
First problem: Overdoing the subtraction principle
First,
I have 3 related questions concerning rolling multiple dice. I have worked them all through. I am interested in confirmation that my reasoning and working is sound.
The first question is:
Say you roll five dice.
- What is the chance that you’ll get at least one 5 and at least one 6?
- What is the probability that the sum of the numbers showing is 5 or less?
My solution:
- It is easier to compute the number of ways of not getting any 5’s or 6’s and subtract these from the number of possible outcomes.
So the number of ways of getting 1 to 4 is 4^5.
The number of ways of getting all 5’s is 1. (There must be at least one 6.)
The number of ways of getting all 6’s is 1. (There must be at least one 5.)
Then the probability is (6^5 – 4^5 – 1 – 1)/6^5 ≈ 0.868.
- It is easier to compute the number of ways of getting a sum of 6 and subtracting these from the number of possible outcomes.
The only way to get a sum of six is for the six faces to show 1, 1, 1, 1, 2. Clearly, four of the dice must have a minimum value of 1 and so the other must show a 2.
The number of ways of getting this outcome is 5 (the 2 can appear on any of the five dice with the other 4 showing a 1).
So the probability is 5/6^5 ≈ 0.000643.
There are good ideas here, but some details are wrong.
I answered this one:
Here is part 1:
Say you roll five dice. What is the chance that you’ll get at least one 5 and at least one 6?
You are calculating P(at least one 5 and at least one 6) as
1 – ( P(no 5’s and no 6’s) + P(all 5’s) + P(all 6’s) ).
Why?
You are implicitly saying that the outcomes that do not have at least one 5 and at least one 6 can be partitioned into (a) no 5’s or 6’s; (b) all 5’s; (c) all 6’s. But there are other possibilities, such as, say, 11115 (that is, at least one 5, but no 6’s). So you are not covering all cases.
The idea of subtracting is useful for “at least one” problems, because \(P(\text{at least one }A)=1-P(\text{no }A)\). But this is a little different. He is using the fact that \(P(E)=1-P(\text{not }E)\); but what is “\(\text{not }E\)”?
I might start with the fact that the negation of “at least one 5 and at least one 6″ is “no 5’s or no 6’s”. This is an important fact you may not have learned explicitly: The negation of “p and q” is “not p or not q”. The language of “or” and “and” can be very tricky, both in English and in math! I discussed these ideas in
Part 2 uses the same idea.
Here is part 2:
What is the probability that the sum of the numbers showing is 5 or less?
You are trying to calculate P(sum ≤ 5) = 1 – P(sum > 5); but you seem to forget that the sum can be greater than 6 (in fact, it can be as high as 30).
Hint: What is the lowest possible sum on 5 dice? What is the probability that the sum is 5?
Probably he was thinking of individual values, which can be no more than 6; his idea would be correct if this were about one die.
Corrections
Jonathan replied, with a good diagnosis:
Hi Doctor Peterson,
I can see I have been overzealous with the subtraction principle in an effort to reduce the enumerations necessary. Sadly, it seems I have misapplied it.
For the first part, based on what you have said, even without applying the negation operator of formal logic it is now obvious that, from the total number of outcomes, I need to subtract (the number of ways of getting no 5’s) AND (the number of ways of getting no 6’s), i.e., separately, and not (the number of ways of getting no 5’s AND no 6’s).
So the number of ways becomes: 6^5 – 5^5 – 5^5 = 1526, and so the probability is 1526/6^5 ≈ 0.196.
For the second part, the number of ways that the sum of the numbers is 5 or less is 1, as 5 is the lowest sum possible with 5 dice. So the probability is 1/(6^5) ≈ 0.000129. This is very small, as expected, as the number of times one would get all 1’s is very low.
Is my reasoning more sound than before? In particular, is the approach correct? One day I would like the get the hang of this combinatorics. It sounds a useful and practical pursuit. At the moment it appears that my haste triumphs over more careful reasoning.
He is almost right on part 1, and right on part 2.
I responded:
The first problem:
What is the chance that you’ll get at least one 5 and at least one 6?
Your calculation is
1 – (P(no 5’s) + P(no 6’s)).
But the subtraction double-counts cases where there are neither 5’s nor 6’s.
Keep in mind the formula for “or”: P(A or B) = P(A) + P(B) – P(A and B). What you want is
1 – (P(no 5’s or no 6’s)).
What he did applies when two events are mutually exclusive, so they can’t both happen. The key idea here, in its most general form, is the Inclusion-Exclusion Rule.
The second problem:
What is the probability that the sum of the numbers showing is 5 or less?
Your answer is correct. The only way to roll 5 or less is to roll five 1’s.
The wording hides a trivial question, by distracting your with “or less”.
The first problem is perhaps harder than it looks; the second is easier than it looks. Both are devious.
As to getting the hang of it, I’ll just remind you that my haste triumphs over careful reasoning more often than you see! My first (in my head) answer to your first problem was less correct than yours was, because I totally missed a fact or two. But I caught it before I wrote anything down, much less typed it … though I think there were a couple erasures along the way.
I often remind students to take their time; and also not to trust what they think without writing it down.
Jonathan now got it:
I see the error in part 1. I sketched a Venn diagram and this revealed all. In fact is was an ‘inverse’ Venn diagram, where the circles represent (NOT 5) and (NOT 6) and the intersection (NOT 5) AND (NOT 6).
What I need is (total number of outcomes) – (number of ways of getting no 5’s) – (number of ways of getting no 6’s) + (number of ways of getting no 5’s AND no 6’s).
This is 6^5 – 5^5 – 5^5 + 4^5 = 2550
The probability is then (6^5 – 5^5 – 5^5 + 4^5)/(6^5) = 0.328
Does this look correct? I feel you are going to tell me there is an easier way.
He was right.
His Venn diagram may look like this:
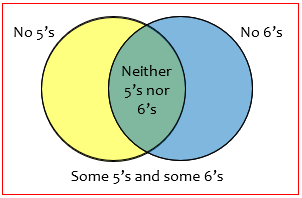
The event “at least one 5 and at least one 6” is the outer region; its complement is the union, “no 5’s or no 6’s”, whose probability is the sum of “no 5’s” and “no 6’s”, minus the overlap, “no 5’s and no 6’s”.
It could also be done in positive form:
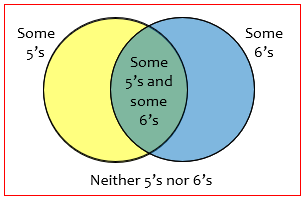
But it would be harder to solve this way.
Second problem: Highest number
In the game of Phigh, each player rolls three dice; their score is the highest number that appears.
- What is the probability of scoring 1?
- What is the probability of scoring 2?
- What is the probability of scoring 2 or less?
- Your opponent scored 4. What is the probability that you’ll win (that is, score 5 or 6)?
My solution:
The rules of the game, as given, are a little vague. So I have made the following assumptions.
(a) What is meant by ‘the score’ is the highest face value appearing on all 6 dice and not the total on all 6. So the score is that considering both players and not the score on just one player’s dice. If the score was considered to be the sum of the values on each die, then the solution to parts 1, 2, and 3 would be trivially 0; so that is clearly not what is meant.
(b) In part 4, I have taken the score to be that of an individual, i.e., the highest face value on just the three dice of one participant.
He showed work, but I’ll omit it here (along with comments on it) because his interpretation of the entire problem is wrong.
In my initial response, I commented on this one:
I do notice that you are misinterpreting this:
In the game of Phigh, each player rolls three dice; their score is the highest number that appears.
The English could have been improved (the word “their” is probably meant to be a non-gendered singular, but makes it sound as if it were not about one individual); but in a game it should be clear that each player gets a score, so it doesn’t really make sense to say
What is meant by ‘the score’ is the highest face value appearing on all 6 dice and not the total on all 6. So the score is that considering both players and not the score on just one player’s dice.
This is definitely not about a total, but it is also clearly about one player’s dice. Part (4) makes this obvious; the scores they are talking about are individual.
So, if I roll 3 dice, what is the probability that the highest of the three is 1?
After the question was submitted separately, Doctor Rick answered:
Much of your work looks good given your interpretation of the problem — but like Doctor Peterson, I believe your interpretation is incorrect.
It makes no sense to me to interpret the “score” in different ways in different parts of the problem. Since in part 4, it is clear that each player has an individual score, I would carry this into parts 1-3 as well. I would rewrite the introductory sentence like this:
In the game of Phigh, each player rolls three dice; the highest number appearing on one of these dice is the player’s score.
How will this change your answers to parts 1, 2, and 3?
As for part 4, there is a better solution method. Think about another way to say “the highest number is NOT either 5 or 6.”
Solving the right problem
Jonathan replied:
Hi Doctor Rick.
Thank you for your comments.
For part 1 [score of 1], the total number of outcomes is now 6^3, so the probability of scoring 1 is 1/(6^3) = 0.00463 to 3 s.f.
For part 2 [score of 2], a player can score one 2 in three ways, two 2’s in three ways, and three 2’s in one way. In all cases, the other die or dice must have the value 1. The total number of outcomes is again 6^3. So the probability is (3 + 3 + 1)/(6^3) = 7/(6^3) = 0.032 to 3 s.f.
For part 3, the number of ways of scoring 2 or less is the number of ways of scoring 1or 2. From parts 1 and 2, this is: ((3 + 3 + 1) + 1)/(6^3) = 0.037 to 3 s.f.
For part 4, using the method of part 2, the number of ways of scoring one 5, two 5’s and three 5’s is three, three and one, respectively. Similarly for scoring 6’s.
Now consider what value or values the other die or dice can have in each case.
For one 5 or 6, it must be 4^2; for two 5’s or 6’s it must be: 4^1; and for three 5’s or 6’s it is not relevant.
So, the number of ways of getting a 5 or a 6 is: (3 * (4^2)) + (3 * (4^1)) + 1) * 2 [multiply by 2 because I can have 5’s or 6’s].
So the probability is ((3 * (4^2)) + (3 * (4^1)) + 1) * 2)/(6^3) = 0.565 to 3 s.f.
Concerning your suggestion about NOT (5 OR 6), This is the same as (NOT 5) AND (NOT 6).
Well, the highest number (NOT 5) AND (NOT 6) leaves me with the highest number 4 or less. I’m not sure if this is easier.
His work on part 4 gets the probability of scoring 5 right, but it is not the same for 6.
Doctor Rick responded:
I get the same answers as you for parts 1, 2, and 3: 1/63, 7/63, and 8/63.
For part 4, I get a different answer. I am not inclined to try to figure out where your method went wrong, because the method I am hinting at is much easier and less error-prone.
You are correct that “the highest number is not 5 or 6” is equivalent to “every number is 4 or less.” However, apparently you have not yet seen how easy it is to find the probability that every number is 4 or less.
Notice that part 3 can be expressed in the same form: the probability that every number is 2 or less. There is an easier way to solve that part, too — easier than adding the results from parts 1 and 2. Just looking at the answer to that part (as a fraction) might be enough to give you an idea.
Here is another hint, if you need it: Consider how you found the denominator for all of these probabilities.
Jonathan replied:
Thank you Doctor Rick.
This seems to typical of the way I approach these problems. Once I pursue a method I continue with it by hook or by crook.
Yes, the solution to part 3 is simply (2^3)/(6^3) = 0.037 to 3 s.f. What is particularly vexing to me is that I have used this observation in this problem and elsewhere.
So, of course, for part 4: the number of ways to arrive at 4 or less is 4^3 = 64. Then the number of ways to score 5 or 6 is 6^3 – 4^3 = 152, resulting in a probability of 152/6^3 = 0.704 to 3 s.f.
Is this now correct?
If so, I would still like to pursue my original method, but I expect I will have to do that on my own, which is OK: it will be good for me. At least I now have a means of verifying the method.
Perseverance is something we love to see!
Doctor Rick responded again:
Yes, that’s the answer I got. You caught on to the idea I wanted you to see. Great!
As to your other method, without digging deeply into it, my first expectation was that you would be overcounting; but your answer was too low, so it appears that you undercounted — that you missed some possibilities. Of course, it’s possible that you both overcounted and undercounted — counting some possibilities more than once, but missing even more possibilities. Have fun trying to fix it!
I should add that, in combinatorics and probability, we really prefer to have more than one solution method (as long as they give the same result). It gives us much more confidence that we haven’t made an error. So I am all for your trying to get the other method to work.
Correcting his original method
Jonathan replied:
Hi Doctor Rick,
I have taken your advice and pursued the other method.
What I overlooked when I considered the number of ways of obtaining one, two or 3 6’s is that the other die or dice can have a value of 5, and not just 1 to 4, as this will also give me a score of 6.
So the sum becomes (3*(4^2) + 3*(4^1) + 1) + (3*(5^2) + 3*(5^1) + 1) = 61 + 91 = 152, in agreement with the other method.
It took a while to see it but I am pleased I persevered and it has at least taught me something.
Thank you for your help and for the encouragement.
Doctor Rick responded again:
Good! Let me just “think out loud” a bit about your method. In such a method, it’s important that we make sure we have a valid partition of the possibilities — that is, a collection of subsets such that every possibility is in exactly one of the subsets. Here is how I see the partition:
One 5, two 4 or less: 3·42 = 48 Two 5's, one 4 or less: 3·4 = 12 Three 5's: 1 One 6, two 5 or less: 3·52 = 75 Two 6's, one 5 or less: 3·5 = 15 Three 5's: 1 -- 152That looks like a solid partition to me.
Jonathan closed:
That is an interesting way of representing it. So I used Boolean algebra and you used some set theory. I can see there are several inter-related branches of discrete mathematics one can use to tackle problems like these. It has been an interesting and fruitful adventure.
Thank you for your help and suggestions.
Third problem: Roll a 7 twice in 10 rolls?
The last problem had a different sort of trick.
Suppose you roll a fair die 10 times.
- What is the probability that you’ll roll a ‘7’ exactly twice?
- Which of the following is most likely:
(a) you roll exactly one 6;
(b) you roll exactly two 6’s;
(c) you roll exactly three 6’s;
(d) you roll no 6’s.
My solution.
1. I cannot make sense of this question. The probability is 0, as there is no 7. If it is taken to mean the sum of two consecutive throws is 7, then I would need to consider the number of ways of getting a seven from two throws; then there are five ways of positioning the two adjacent throws within the 10 throws.
Additionally, I would need to consider the number of ways the other 8 dice can come up, which is 6^8. …
I am not convinced that this is what the question is after, and so the initial probability of 0 still stands.
2. Consider each outcome in turn.
(a) The 6 can appear on any one of the 10 throws. Then the other throws must have a value of 1 to 5. So the number of ways is 10*5^9. Probability is then (10*5^9)/6^10 ≈ 0.323.
(b) The two 6’s can appear on any two of the 10 throws. So there are (10 choose 2) = 10!/8!2! = 45 ways. For each of these, the other 8 throws must have a face value of 1 to 5.
So the probability is (45*5^8)/6^10 ≈ 0.291.
(c) The three 6’s can appear on any three of the 10 throws. So there are (10 choose 3) = 10!/7!3! = 120 ways. For each of these, the other 7 throws must have a face value of 1 to 5.
So the probability is (120*5^7)/6^10 ≈ 0.155.
(d) The number of ways of getting no 6’s is the number of ways that each of the other die have a value 1 to 5. This is 5^10. So the probability is (5^10)/6^10 ≈ 0.162.
Thank you for any comments you may have on my solution.
On part 1, I replied,
You’re right that the probability is 0; that makes perfectly good sense! There is no mention of sums of consecutive throws, so I wouldn’t even consider that. And I don’t even want to try answering your reworded question, which is more complicated than it’s worth, just as you’ve indicated.
In probability classes, we do sometimes ask trivial questions, because sometimes it matters.
As for part 2,
I agree. This is just a binomial distribution problem.
