Here is a short problem with several levels of difficulty. The problem itself is poorly designed, as we’ll see, but still provides several useful lessons, dealing with measurement, rounding, and ratios.
Finding proportions on a pie chart
It came from Rawan in mid-September:
How do I solve this problem? I don’t understand it.
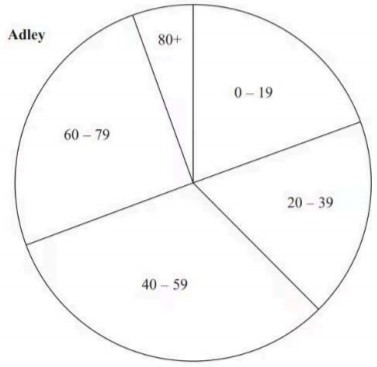
The pie charts give information about the ages, in years, of people living in two towns, Adley and Bridford.
Diagrams accurately drawn
The ratio of the number of people living in Adley to the number of people living in Bridford is given by the ratio of the areas of the pie charts.
What proportion of the total number of people living in these two towns live in Adley AND are aged 0-19? Give your answer correct to three significant figures.
I have no work to show.
It’s far more common to find problems stating “not drawn to scale” so that you will not be tempted to measure what you see; here, measuring is clearly the point. And that is the difficulty.
Approaching the problem
Doctor Rick answered, explaining the meaning of the problem so Rawan could get started:
Hi, Rawan, thanks for writing to the Math Doctors.
One important point in the problem is the note “Diagrams accurately drawn.” This means that you can find information from the figures by making measurements. You will need a ruler and a protractor. (You could do without the protractor if you know trigonometry, but I imagine the problem is not meant to assume this knowledge.)
Another important point is the comment, “The ratio of the number of people living in Adley to the number of people living in Bradford is given by the ratio of the areas of the pie charts.” You should be aware of the fact that the same is true of any two regions in a pie chart; because of the comment, it is true of any two regions in either or both pie charts.
What can you do with this guidance? Do you know how to find the area of a sector of a circle? If this doesn’t seem familiar to you, what do you know about pie charts?
In a pie chart, the values represented are proportional to the central angles, and therefore also to the arc lengths, and to the areas, since \(s=r\theta\) and \(K=\pi r^2\cdot\frac{\theta}{2\pi}=\frac{1}{2}r^2\theta\) (when the angle is given in radians). This makes the entire problem consistent; all areas are proportional to the populations they represent.
Rawan replied, this time with a solution:
The answer I got (rounded to 3 significant figures) was 11.3, is this correct?
Assuming (because I can’t measure accurately due to only having a soft copy of the question) that the angle for the (0-19) part in the Adley pie chart is 70°, and the radius of the Adley circle is 1.6 cm, and the Bridford circle’s radius is 1.4 cm.
First I found the Sector Area [ (θ/360) * π * (r2) ] of the (0-19) part in Adley, so (70/360) * π * (1.62) = 1.6 cm2 .
Then I found the Total Areas (πr2) of both pie charts, I got 8.04 cm2 for Adley, and 6.16 cm2 for Bridford. The total of the areas is 14.2 cm2.
The question says that the areas can basically be used as the number of people in each town’s pie chart or sector (proportions are equal, and since we do not have exact values we use these directly).
Since we are looking for the proportion, I should get the fraction of the Sector Area of the (0-19) part in Adley over the total areas of both pie charts, multiplied by 100. And that will be, 1.6/14.2 = 0.11267, times 100, that will be: 11.267 = 11.3% (rounded to 3 s.f.). Is this correct, or did I do something wrong?
There is very good thinking here. In particular, rather than try to convert areas to actual populations (which, of course, we can’t do without more information), he recognizes that he can use ratios of areas directly. His answer is almost right, apart from two issues: measurements, and rounding.
I suspect he may have done his measuring on a phone screen, considering the size; this would also make it difficult to measure the angle.
Measuring woes
Doctor Rick responded:
Thanks for showing your work. I have a protractor, and the angle does appear to be 70°. On my laptop screen, the radii of the two circles are 4.5 cm and 3.75 cm. Based on these figures, I do not get the result you obtained. Let me now check your work …
Of course we have different measurements for the radii, but the ratio of the radii ought to be the same, within measurement precision. From your measurements I get a ratio (Bridford to Adley) of rB/rA = 7/9 = 0.778, whereas from my measurements I got a ratio of 5/6 = 0.833. That’s quite a big difference, and could easily account for the difference in our answers, as the ratio of areas is the square of the ratio of radii.
In my calculations I took a shortcut, working with ratios all the way. Using your data, I find the ratio we seek to be 0.1101, close to your result (but not the same – see below). So I think your method was valid; the main error is in the measurements.
Here is how we’d measure the angle, which is indeed (about) 70°:
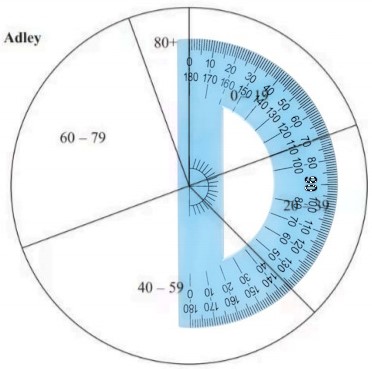
On my screen, I read the radii as 5.2 cm and 4.4 cm, for a ratio of 11/13 = 0.846! Rawan’s ratio of 1.4/1.6 is 7/8 = 0.875; Doctor Rick appears to have misread that as 1.4/1.8 = 7/9 = 0.778. And his own ratio of 3.75/4.5 reduces to 5/6 = 0.833. Taking this into account, they are not very far apart; but clearly, we can’t expect an answer correct to three significant figures based on such uncertain measurements. We’ll get back to that.
On the other hand, it’s interesting that our measurements all reduce to fairly simple fractions, which is likely the intent of the problem; possibly the actual size on paper is meant to be a pair of numbers that most students would agree on, so that they would consider them accurate to 3 significant figures. But that would be a mistake: It is impossible to actually measure either the angle or the radii that accurately with ordinary tools, so this would be a false sense of precision, exactly the opposite of what I would want students to learn! It is not true, even in the classroom, that if you get a whole number, it has to be exactly right.
Looking for other sources of the problem, I found a pdf of a 2017 GCSE exam containing this problem (pag3e 12), and I read the radii there onscreen as 6.3 cm and 5 cm, for a ratio of 50/63 = 0.79365 (which doesn’t reduce nicely). The “answer” given there is “depends on printing size”, which is wrong; as long as the printing is not distorted, the ratio should be the same at any size. But when I use the measuring tool for the downloaded PDF, it gives different measurements:
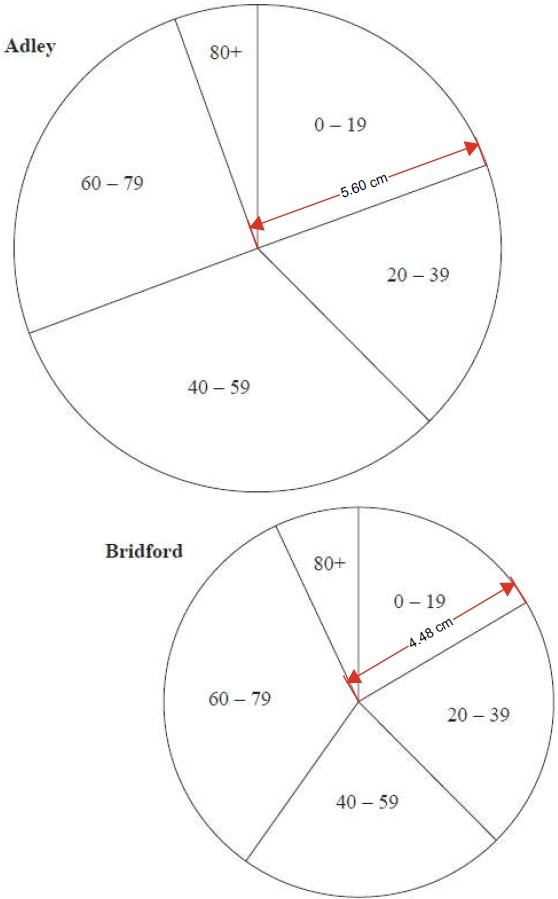
The ratio 4.48/5.60 turns out to be exactly 4/5 = 0.8. If we had measured by hand on a printed copy, we might have called it 4.5/5.6 = 0.8036.
I also found a video solving this problem, which says (apparently from measuring on paper) that the radii are 5 cm and 4 cm (the sort of nice numbers I expected), which again gives a ratio of 4/5 = 0.8. Yet there I measure the radii onscreen as 5.4 cm and 3.7 cm, with a ratio of 0.685. Clearly, it isn’t valid to measure anything on a screen!
Rounding issues
However, it appears that not only did you have only two significant figures in your measurements, you also rounded to two significant figures in your work. This will not result in three significant figures of accuracy in the result; you see that even using your measurements, my answer does not match yours to three significant figures.
I wonder if accuracy was the point of this exercise! Three significant figures is a lot to ask when the numbers are not given to you; it takes care in measuring and in calculating.
If we use Rawan’s numbers, but avoid rounding in intermediate work, then his work looks like this:
$$\text{Sector area }=\frac{70}{360}\pi(1.6^2)=1.56381…\\\text{Adley area }=\pi(1.6^2)=8.04247…\\\text{Bridford area }=\pi(1.4^2)=6.15752…\\\text{Total area }=8.04247…+6.15752…=14.19999…\\\text{Proportion }=\frac{1.56381…}{14.19999…}=0.11012…\approx11.0\%\text{ to 3 sf}$$
If we use Doctor Rick’s numbers, but avoid rounding in intermediate work, then his work looks like this:
$$\text{Sector area }=\frac{70}{360}\pi(4.5^2)=12.37002…\\\text{Adley area }=\pi(4.5^2)=63.61725…\\\text{Bridford area }=\pi(3.75^2)=44.17864..\\\text{Total area }=63.61725…+44.17864…=107.79589…\\\text{Proportion }=\frac{12.37002…}{107.79589…}=0.11475…\approx11.5\%\text{ to 3 sf}$$
If we use the (apparently intended) radii of 4 and 5 cm, treating them as if they were exact, and avoid rounding in intermediate work, then the same method looks like this:
$$\text{Sector area }=\frac{70}{360}\pi(5^2)=15.27163…\\\text{Adley area }=\pi(5^2)=78.53981…\\\text{Bridford area }=\pi(4^2)=50.26548…\\\text{Total area }=78.53981…+50.26548…=128.80529…\\\text{Proportion }=\frac{15.27163…}{128.80529…}=0.11856…\approx11.9\%\text{ to 3 sf}$$
But if I had designed the problem, I might have given full credit to a student whose final answer was, “Because I don’t have suitable tools to measure to three significant figure accuracy, the problem can’t be answered as specified.” One can give an answer with three significant figures of precision, but not correct to three significant figures! Accuracy and precision are not the same thing, and if the problem is intended to teach or assess the concept of precision, then it fails.
Using ratios: making a formula
Rawan wanted additional help:
How do you find the ratios though? I couldn’t figure them out. For me the measurements don’t matter right now since this is only for practice, but is my actually method practical/correct? Is there a easier way to figure this out or could you please explain the steps of this problem.
Doctor Rick replied:
As I said, your method is fine. It is what I suggested. My method using ratios doesn’t save a lot of work; it just eliminates two multiplications by π (pi). However, ratios are very useful in general, so I will explain what I did. I don’t know how much you know about ratios and proportions, or algebra, so some of this may be very familiar and some may be new to you.
First, we’ve used the fact that in a pie chart, the quantity represented in the chart (population of an age group, in our case) is proportional to the area of a sector. We can also say that the quantity is proportional to the central angle of the sector. This is because the area of a sector is proportional to the central angle; you used this fact when you took the area of a sector with central angle 70° to be 70/360 times the area of the circle. (The central angle of a full circle is 360°.)
This was part of Rawan’s good thinking.
I also mentioned that the ratio of the areas of two circles equals the ratio of the squares of their radii. Let’s give names to the various quantities we’ll be working with: Let A be the area of circle A, and let B be the area of circle B. Also call the area of a sector of circle B by the name S, and call its central angle θ. If the radii of the two circles are rA and rB, then the areas of the two circles A and B are
$$\frac{B}{A}=\frac{\pi r_B^2}{\pi r_A^2}$$
I can cancel the π’s and rearrange using algebra to get
$$\frac{B}{A}=\frac{r_B^2}{r_A^2}=\left(\frac{r_B}{r_A}\right)^2$$
This shows that the ratio of the areas of the circles is the square of the ratio of their radii. You see how all this saves is two multiplications by π, but it has broader application. It is true in general that the areas of any two similar figures are proportional to the squares of any linear dimension of the figures. For instance, the areas of two circles are proportional to the squares of their circumferences, or the squares of their diameters; the areas of two equilateral triangles are proportional to the squares of their altitudes; etc.
Knowing this makes it unnecessary to even write out the fractions (and risk missing something in the calculations).
Putting these ideas together, we can come up with a formula. Here’s how. First, we have the area of the sector of circle A:
$$S=\frac{\theta}{360^\circ}\cdot A$$
We want to find the ratio S/(A + B):
$$\frac{S}{A+B}=\frac{\theta}{360^\circ}\cdot \frac{A}{A+B}=\frac{\theta}{360^\circ}\cdot \frac{r_A^2}{r_A^2+r_B^2}$$
We could use this as it is, or simplify a little if we prefer:
If you know enough algebra, you’ll know that we can divide the numerator and denominator of the fraction by rA2 to get
$$\frac{S}{A+B}=\frac{\frac{\theta}{360^\circ}}{1+\left(\frac{r_B}{r_A}\right)^2}$$
That’s our formula. To solve your problem, using your measurements, the ratio of radii is rB/rA = 1.4/1.6 = 7/8, so
$$\frac{S}{A+B}=\frac{\frac{70}{360}}{1+\left(\frac{7}{8}\right)^2}=0.11012…\approx11.0\%$$
Using my measurements, the ratio of radii is rB/rA = 3.75/4.5 = 5/6, so
$$\frac{S}{A+B}=\frac{\frac{70}{360}}{1+\left(\frac{5}{6}\right)^2}=0.11475…\approx11.5\%$$
And using the “official” measurements, the ratio of radii is 4/5, so
$$\frac{S}{A+B}=\frac{\frac{70}{360}}{1+\left(\frac{4}{5}\right)^2}=0.11856…\approx11.9\%$$
That is presumably the intended answer.
All three of these answers agree with what we found Rawan’s way.
Does this help? As I said, a lot depends on how much you know about proportions, and about algebra, so we could go further into any parts that aren’t clear yet, if you’d like.
This evidently was enough.
Using ratios without a formula
There are, as usual, several other ways we could do this. For example, we could use ratios in much the same way, but without making a formula:
If the radii are 5 and 4, then the areas have the ratio \(A:B=5^2:4^2=25:16\), and we can convert this part-to-part ratio to a part-to-whole ratio \(\frac{A}{A+B}=\frac{25}{25+16}=\frac{25}{41}\). The 0-19 group in A is \(\frac{70}{360}=\frac{7}{36}\) of A, and therefore \(\frac{7}{36}\cdot\frac{25}{41}=\frac{175}{1476}\approx0.11856\) of the whole.