To finish up this long series on the order of operations, I want to look at where the “rules” came from, which will also demonstrate why some aspects are not fully agreed upon, finishing up the discussion from last time.
The “rules” are only descriptive
First, here are a couple paragraphs from the 2017 answer I discussed last time (Even More on Order of Operations), that transition to this final topic:
In talking about the extra “juxtaposition” rule taught in some textbooks, I pointed out,
What many people don't realize is that the "rules" we teach are only an attempt at DESCRIBING what mathematicians did for a long time without explicitly stating what rules they were following. They do not PRESCRIBE what inherently must be done, a priori. In just the same way, English grammar came long after English itself, and has sometimes been taught in a way that is inconsistent with actual practice, in an attempt to make the language seem perfectly rational.
At this point, I referred to the post I’ll be discussing below, on the history of the order of operations. Then I concluded,
In my opinion, the rules as usually taught are not the best possible description of how expressions are evaluated in practice. (This is supported by a recent correspondent who found articles from the early twentieth century arguing that the rules newly being taught in schools misrepresented what mathematicians actually did back then.) Unfortunately, for decades schools have taught PEMDAS as if it must be taken literally, so that one must do all multiplications and divisions from left to right, even when it is entirely unnatural to do so. The better textbooks have avoided such tricky expressions; but others actually drill students in these awkward cases, as if it were important.
I’ll examine that 1917 article later.
So who made the rules? Nobody.
We’ve often been asked where the rules came from. The fullest answer we’ve given to that question was to this version in 2000:
History of the Order of Operations I was teaching a computer class and the history of order of operations came up. Where, when and with whom did the order of operations first originate? Was it the Greeks or Romans? Thank you! There is a whole class waiting to hear the answer.
The problem is that not much is written about this history; I had to pull a few ideas (some of them just speculations) from a variety of areas. My answer is, in fact, given as a reference in the Wikipedia article on the subject. I began:
The Order of Operations rules as we know them could not have existed before algebraic notation existed; but I strongly suspect that they existed in some form from the beginning - in the grammar of how people talked about arithmetic when they had only words, and not symbols, to describe operations. It would be interesting to study that grammar in Greek and Latin writings and see how clearly it can be detected.
As mathematicians through the 17th century gradually moved from stating equations entirely in words, to modern symbolic notation, the grammar of the symbols was part of that development, and likely carried along some of the grammar of their languages. For a quick look at what some of the early notations looked like, see here. Every writer used a slightly different notation, which he explained at the beginning of a book or chapter.
Subsequently, mathematicians just informally and tacitly agreed on how to read their various notations; and textbook authors formalized the “rules”, largely in the 1800’s.
At the other end, I think that computers have influenced the subject, so that it is taught more rigidly now than it used to be, since programming languages have had to define how every expression is to be interpreted. Before then, it was more acceptable to simply recognize some forms, like x/yz, as ambiguous and ignore them - something I think we should do more often today, considering some of the questions we get on such issues.
Many people have written to us, convinced that the rules had changed since they were in school. That is, in fact, possible in some areas! Computers need well-defined rules more than people do, so some details that humans had had no trouble working around were formalized in computer languages, and some of that has leaked back into ordinary mathematical writing and teaching.
I spent some time researching this question, because it is asked frequently, but I have not found a definitive answer yet. We can't say any one person invented the rules, and in some respects they have grown gradually over several centuries and are still evolving.
We’ll see some of that current evolution at the end.
Hierarchy and grouping
The easiest and earliest part seems to have been the central hierarchy of operations:
1. The basic rule (that multiplication has precedence over addition) appears to have arisen naturally and without much disagreement as algebraic notation was being developed in the 1600s and the need for such conventions arose. Even though there were numerous competing systems of symbols, forcing each author to state his conventions at the start of a book, they seem not to have had to say much in this area. This is probably because the distributive property implies a natural hierarchy in which multiplication is more powerful than addition, and makes it desirable to be able to write polynomials with as few parentheses as possible; without our order of operations, we would have to write
ax^2 + bx + c
as
(a(x^2)) + (bx) + c
It may also be that the concept existed before the symbolism, perhaps just reflecting the natural structure of problems such as the quadratic.
What I’ve said here is closely related to the reasons for the order of operations discussed in Order of Operations: Why These Rules?.
You can see an example of early notation in "Earliest Uses of Grouping Symbols" at: http://jeff560.tripod.com/grouping.html where the use of a vinculum (an early version of parentheses) shows, both in its presence (around an additive expression) and its absence (around the multiplicative term "B in D") that the rules were implicitly followed: In Van Schooten's 1646 edition of Vieta, ________________ B in D quad. + B in D is used to represent B(D^2 + BD).
The example is also found in Cajori’s A History of Mathematical Notations, Vol 1, p. 182, and again (in a discussion of aggregation, or grouping, symbols) on p. 386.
At this point in the development of notation there was a mixture of words and symbols; multiplication was indicated by the word “in” (I’m not sure why!), and not yet by any of our current symbols (much less by juxtaposition). But in order to ensure that the two terms are added before the multiplication by B, they must be grouped; whereas under the vinculum we clearly have two terms, each formed by multiplication before the addition is performed.
Not always consistent
2. There were some exceptions early in this development; in particular, math historian Florian Cajori quotes many writers for whom, in the special case of a factorial-like expression such as
n(n-1)(n-2)
the multiplication sign seems to have had some of the effect of an aggregation symbol; they would write
n * n - 1 * n - 2
(using a dot or cross where I have the asterisks) to express this. Yet Cajori points out that this was an exception to a rule already established, by which "nn-1n-2" would be taken as the quadratic "n^2 - n - 2."
This reference is to Cajori Vol. 1, p. 396, where he says, “In \(n\cdot n-1\cdot n-2\), or \(n\times n-1\times n-2\), or \(n, n-1, n-2\), it was understood very generally that the subtractions are performed first, the multiplications later, a practice contrary to that ordinarily followed at that time.”
There was also an early notation in which a multiplication would be replaced by a comma to indicate aggregation:
n, n - 1
would mean
n (n - 1)
whereas
nn-1
meant
n^2 - 1.
This use of commas is explicitly mentioned on page 390. It does seem helpful to have a symbol that combines multiplication and grouping for cases where that is appropriate. Still, this is all a special case distinct from the multiplication-first order that was already well-established.
Multiplication and division
If the “rules” evolved gradually through usage, it should not be surprising that some are still not fully settled:
3. Some of the specific rules were not yet established in Cajori's own time (the 1920s). He points out that there was disagreement as to whether multiplication should have precedence over division, or whether they should be treated equally. The general rule was that parentheses should be used to clarify one's meaning - which is still a very good rule. I have not yet found any twentieth-century declarations that resolved these issues, so I do not know how they were resolved. You can see this in "Earliest Uses of Symbols of Operation" at: http://jeff560.tripod.com/operation.html
Cajori makes this statement on page 274.
Starting to teach rules
4. I suspect that the concept, and especially the term "order of operations" and the "PEMDAS/BEDMAS" mnemonics, was formalized only in this century, or at least in the late 1800s, with the growth of the textbook industry. I think it has been more important to textbook authors than to mathematicians, who have just informally agreed without needing to state anything officially.
By “this century” I meant, somewhat belatedly, the 20th century. I don’t have specific information on the earliest uses of these terms, but I’ll get to one evidence of it below.
The implicit multiplication controversy
The rules were never decreed “officially”, and even now are unstable, as some parts are not taught consistently (the topic of the last post):
5. There is still some development in this area, as we frequently hear from students and teachers confused by texts that either teach or imply that implicit multiplication (2x) takes precedence over explicit multiplication and division (2*x, 2/x) in expressions such as a/2b, which they would take as a/(2b), contrary to the generally accepted rules. The idea of adding new rules like this implies that the conventions are not yet completely stable; the situation is not all that different from the 1600s.
As in early writings on symbolic algebra, it is still necessary to state the rules one is using!
Natural rules vs. artificial rules
I concluded that some rules are inherent in the way operations work, and are clearly appropriate, while others are more debatable:
In summary, I would say that the rules actually fall into two categories: the natural rules (such as precedence of exponential over multiplicative over additive operations, and the meaning of parentheses), and the artificial rules (left-to-right evaluation, equal precedence for multiplication and division, and so on). The former were present from the beginning of the notation, and probably existed already, though in a somewhat different form, in the geometric and verbal modes of expression that preceded algebraic symbolism. The latter, not having any absolute reason for their acceptance, have had to be gradually agreed upon through usage, and continue to evolve.
That’s where I left it in 2000.
The rules were never quite right
In 2017 we had a long discussion (never archived) with a reader named Karen, in the course of which there was a reference to an interesting article by N. J. Lennes in the American Mathematical Monthly of February 1917: Discussions: Relating to the Order of Operations in Algebra. Here are my comments on it:
I agree with some aspects of the article, and in fact said something like it both in my "History of the Order of Operations" and in my comment to you about what my ideal rules would be. When I answer questions about the issue, I take the usual teaching, and the current contradictory rules, for granted, and don't generally dig into whether the rules make sense. But the article is about exactly what I usually leave unsaid.
I generally talk about what we should do given the way the order of operations is currently taught, rather than what it would be if I had my say. Here, I have my say, because that is what Lennes is doing at a time in history when that was easier.
After quoting some of what I said above on the history, specifically on disagreements over the order of multiplication and division, I continued:
One interesting thing about Cajori's comment is that he only talks about the order of the obelus (÷) and the explicit multiplication sign (Greek cross, ×), and doesn't mention expressions combining the obelus and implicit multiplication (juxtaposition). The same is true of all the references in the Earliest Uses page except the modern example. The article you found (which I haven't seen before) is from a little before Cajori, and the first section likewise does not mention juxtaposition. It is my impression that the "rules" for order of operation (which as I have mentioned elsewhere are, like many prescriptive "rules" of grammar, really descriptions rather than actual underlying rules) were developed in such a context, using only explicit multiplication, where it feels reasonable since all the signs are the same size! When you start using juxtaposition (as in the second section of your article), things change.
For instance, in \(2\div 3\times x\), the symbols look similar and separate the numbers by similar distances, whereas in \(2\div 3x\), the multiplication appears “tighter” and is naturally treated as a single unit. And the latter is where Lennes, but not Cajori, focuses his attention:
As Lennes points out, the "rules" that were (and are now) taught as if they were laws of nature, do not actually reflect what was found in real use, *in cases when juxtaposition is used for multiplication*. The whole idea is really a false extrapolation from what is done in easy cases to a general rule, making everything seem neater that it really should be. (Educators have made that same sort of mistake in other areas as well.) That has led to generations of students being taught a simplistic set of rules that really don't work in mathematicians' own writings. That, ultimately, is what leads to the ambiguity we have been discussing, as people have been forced to fill in the gap between rules and reality in whatever way they can.
When rules don’t fit nature, people don’t follow them.
This is not unlike pseudo-rules of grammar like “never end a sentence with a preposition” that are based on false assumptions about how things work, and not on how real people talk.
Lennes says that Chrystal (whoever he is -- I haven't been able to find such a textbook that might have been an early source of the "order of operations") is careful never to use an obelus followed by a product (which is true of many modern texts as well), but that others do, and interpret, say, 10bc -:- 12a as (10bc)/(12a), so that they are inconsistent with their own stated rules. (My first exposure to this issue came from students asking about similarly inconsistent modern texts.)
Just as I have said about modern textbooks, the best of them avoided examples like this \(10bc\div 12a\), but those that include them too often failed either to follow their own rules, or to state that they are making an exception, and just evaluate as if it were \(\frac{10bc}{12a}\). Why? Because they think that rules are rules, but they are too human to really follow them.
I disagree with Lennes in his conclusion, however. He says that the rule should be that all multiplications are to be done first. As I have said to you, if I were free to decree the rule, I would have only implicit multiplication done before divisions, and that perhaps only when the division is expressed with the obelus. Lennes gives no examples of following his rule with explicit multiplication combined with an obelus, which I think would be less convincing. So he is perhaps making the same mistake that Chrystal does.
When you use only one type of example, you can fail to show reality, whichever direction that is.
In the end, he comes to the same sort of comparison I make between math and grammar, saying that treating 12a as the divisor is an "idiom" that must be recognized. As he says, this is a matter not of logic but of history -- it is not something that can be proved, or that can be done by consistently following axioms, but by accurately describing actual use. I agree: the rules as taught are not accurate. I support them only because that is what students learn, and with the strong caveats that parentheses must be used to clarify, and that the obelus is best avoided.
I have taken this position (for example, “the alternative rule is not unreasonable”), ever since my first answer to the question, while also warning against ever writing a division followed by a multiplication (of any sort) without clarifying the meaning by parentheses. It was nice to learn that this view went back a hundred years!
Here is what Lennes says:
Idiom is not exactly the right word here, but the idea is important: The order of operations “rules” are not binding, but should only describe actual usage.
Incidentally, Karen also referred to this page by George Bergman,
Order of arithmetic operations; in particular, the 48/2(9+3) question
which as I said, could have been written by me, though its author evidently was new to the issue. As he says of PEMDAS (which he clearly is not familiar with as a teaching tool),
But so far as I know, it is a creation of some educator, who has taken conventions in real use, and extended them to cover cases where there is no accepted convention. … Should there be a standard convention for the relative order of multiplication and division in expressions where division is expressed using a slant? My feeling is that rather than burdening our memories with a mass of conventions, and setting things up for misinterpretations by people who have not learned them all, we should learn how to be unambiguous, i.e., we should use parentheses except where firmly established conventions exist. If expressions involving long sequences of multiplications and divisions should in the future become common, then there may be a movement to introduce a standard convention on this point. (A first stage would involve individual authors writing that “in this work”, expressions of a certain form will have a certain meaning.) But students should not be told that there is a convention when there isn’t.
It’s good to know I’m not alone in my opinions.
The difference between handwriting and typewriting mathematics explains many common confusions.
In typewritten notation, which does not normally include a horizonal line to indicate division, these are the two mutually exclusive forms of the algebraic compound fraction notation that can exist: 48(9 + 3)/2 [where the brackets lie above the division line when handwritten] and 48/2(9 + 3) [where the brackets lie below the division line when handwritten].
48(9 + 3)/2 and 48/2 (9 + 3) or 48/2 x (9 + 3) are the same thing but would all be different ways of indicating in typewriting that the brackets are not below the division line in clear terms. But as soon as you compound the brackets with the 2 it’s now in fraction notation and below the division line in handwriting – in fact it’s the only way to typewrite that accurately and proves the convention.
These are partially equations resolved from BODMAS string notation into the more precise algebraic compound notation used for final solution of a written equation. The oblique is not a BODMAS string notation symbol but it being difficult to find and type the traditional BODMAS division symbol in many typed media has led to ambiguity over what an author intends when using an oblique. Traditionally the oblique was and is an acceptable final form algebraic compound notation symbol used to finally record fractions in handwriting that are incapable of further resolution in whole numbers.
Similarly, juxtaposition of letters with numerals without interposing traditional BODMAS string notation symbols such as brackets or multiplication symbols is also an algebraic compound notation convention not a BODMAS string notation convention.
Such conventions and how to convert between them can be as complex as any language but were being taught consistently since at least the beginning of the 1970s in Britain and throughout its former colonies north and south of the equator, i.e. the full span of my education that allows me to attest to this directly. Any confusion over these governing conventions we all were expected to use to translate mathematic equations into our own language within that educational paradigm in order to understand what was intended to be said by the author of the equation is always down to individuals’ imperfect memory of the convention due to lack of frequent use or individuals adopting imprecise homebrew writing conventions later in life and typewriting not being a convenient form of writing in the conventional language of mathematics.
Hi, Andrew.
I think you are largely referring to the “implicit multiplication” controversy that is the focus of the end of this post, and all of the previous post.
When you talk about “typewritten” notation, I assume you mean writing all on one line; “handwriting”, as I understand it, is essentially the same as what I would call “typeset” notation as used in books, and allows what you call “algebraic compound fraction notation” with the horizontal fraction bar. I’m not sure if there are other distinctions you are making. You also talk about “BODMAS string notation” (apparently your own invention, as I find the term used nowhere), which I suppose is the same as typeset notation (found in books) but perhaps all on one line, as you distinguish it from “algebraic compound notation”. These nonstandard distinctions make it hard to follow your point.
You appear to be taking “48/2(9 + 3)” to mean \(\frac{48}{2(9+3)}\), but “48/2 (9 + 3)” with a space to mean \(\frac{48(9+3)}{2}\). I’m not sure whether you think this is prescribed by some rules, or is a mistake. My recommendation is to use parentheses to make it clear, rather than depending on easily missed subtleties of spacing: “48/(2(9 + 3))” vs “(48/2)(9 + 3)”.
I would agree that the tendency to replace the obelus (÷) with a slash or oblique (/) in typing contributes somewhat to students’ tendency to assume that everything that follows is in the denominator, as if the fraction bar were just being tilted. But the same issue is present with the obelus; none of what I have said applies only to the slash. And if you are implying that BODMAS does not apply to typeset notation, I think you are wrong.
Perhaps my main disagreement with you is that you are assuming a universally accepted, prescriptive convention that people simply forget to follow, whereas I believe that the “rules” are (or should be) descriptive, and the difficulty in this area arises largely from their not adequately describing natural usage. There is no authority that sets rules. The conflicts we see are found even between textbooks, not just in typing, and do not on the whole involve the “oblique”. But it may be different in your part of the world.
If you’d like to discuss this at length, you might use the Ask a Question link to make it more convenient.
6/2(2+1). I am finding people see this problem differently. I was taught to do parentheses first using PEMDAS. Therefore 6/2(3)=3(3) is 9. It was argued to me that you work from parentheses out. Therefore 6/2(2+1) = 6/2(3)=6/6=1. Which way would be considered correct and was the process changed with the invention of calculators and computers?
Have you read the previous post, Order of Operations: Implicit Multiplication?, which was about your exact question?
My impression, as discussed there, is that
So which is right? If you’re in school, follow the rules you’re taught; if you’re at work, check what those around you mean by what they write; and if you’re on social media, ignore the nonsense, which is only intended to stir up unnecessary arguments.
Turn that divisor line to the horizontal as intended. Then work the problem.
6. 6-- (1+2) = -- (3) = 3 (3) = 9
2. 2
There’s just one problem with this answer: How do you know what the original author of the expression intended by it? If he is a student in an American school, it is quite possible he intended what you say; but not everyone would.
6/2(1+2) is a monomial
Factors multiplied make a single term.
In my opinion, factors multiplied together making a single term, looks very similar to implied multiplication.
And Euler explains it clearly.
The following was written in 1765.
“It is also plain, that 12mn, divided by 3m, gives 4n; for 3m, multiplied by 4n, makes 12mn. But if this same number 12mn had been divided by 12, we should have obtained the quotient mn.”
Euler p14 Section 1 Elements of Algebra.
Hi, Doug.
You are saying several different things here.
The first claim, that the definition of a monomial settles the question, is wrong; I have discussed here the fact that it can’t be proved mathematically.
The quotation from Hawkes, on the other hand, is an argument from usage, which is valid: Some authors do teach that implied multiplication is done before division, and this is one of the clearer early cases (though he still does not explicitly state such a rule, as I’ll show in response to another of your comments here). By the way, I found several editions of this book available; in this source, your quotation is on page 74.
It’s worth noting that Hawkes wrote around 1910, the time period in which Cajori said there was wide disagreement, as I quoted here.
As for the Euler quotation, which I find here among other places, he doesn’t actually use the notation, so it proves nothing. Anyone would agree that if you divide 12mn by 3m you get 4n; the issue is whether everyone agrees that 12mn / 3m means that. (I think there is good reason to take it that way, just as you say; I just can’t speak for everyone.)
I discussed this matter of what is or is not standard usage here.
I think Mixed Numbers contribute significantly to the idea that implicit operators are applied before explicit operators.
You see 5 3/4 and know it’s 5+3/4, not 5*3/4
You are taught that a variable next to another value is implicitly being multiplied – and as such, the precedence exists with the two values.
I don’t think that’s very relevant. It’s an example where juxtaposition does not mean multiplication! If you mean that it’s a reminder that in algebra it normally does, that doesn’t say anything about precedence relative to other multiplications.
I say that the only thing that matters is consensus; and the problem is that, at least in American schools, students tend to see an artificial consensus on what is ultimately the wrong rule. Until we have a genuine consensus, we just have to write expressions defensively.
Respectfully, sir, the only thing that matters is the real world consequences of the answer. When calculating the trajectory of a rocket to the moon, which one lands one safely on the moon and which one sends the rocket into the sun? Consensus doesn’t matter here, real world consequences do.
I think you are missing the point. Consensus about notation doesn’t matter if you are just doing the math yourself; you can make up any notation you want, as long as you mean the right thing. But it is essential for communication, which is what this discussion is all about.
But you chose an interesting example. Have you never heard of the Mars shot that failed because different project groups lacked consensus on the format of data (namely, what units to use)? If two people share a formula but interpret it differently, then everything goes wrong.
Another interesting observation: juxtaposition is fine as long as it is clearly understood that variables are always a single character. That is, 2ab can only mean 2 * a * b, not 2 * [the variable] ab. Now that so many people are computer-literate, one-character variables are going out of fashion. So why should we continue to accept juxtaposition. It’s certainly not accepted with numeric digits!
Having said that, I come from the generation for which variables WERE always one character and implied multiplication DID have priority — and also from a l-o-n-g career with computers.
It’s important to keep in mind that computer programming has its own separate issues, and does not directly influence what should be done in writing mathematics. Most languages don’t support juxtaposition as implying an operation, just because of the way they are designed. And we can write mathematical expressions using multi-character variables (often when communicating to non-mathematicians, as in financial formulas), but obviously we don’t use juxtaposition when we do so. Within mathematics, single-character variables keep things concise, so I don’t think they are going away.
So, do you think elementary and secondary schools should stop teaching the Order of Operations as they do? I’ve taught in three provinces in Canada and one in China and it’s been consistent to treat multiplication and division as the same and perform operations left to right. Like, for example 48/3 = 48*(1/3) so wouldn’t it follow that 48/3(2+1) = 48(1/3)(2+1)?
I’m so used to this method I find it so difficult to see the ambiguity.
Your reasoning is good, and convincing when you just think logically, as I did in Order of Operations: Common Misunderstandings. The only problem is that others (including many mathematicians) see juxtaposition as being different, and with good reasons that I also find convincing! We aren’t going to convince everyone to take the same perspective; and each rule is likely to be forgotten in particular circumstances where it just feels unnatural. Nor could we convince everyone not to use juxtaposition at all, which would be another solution if it weren’t so inconvenient!
I think the only thing I’d want taught differently is to be aware that others may read such an expression differently (whether it’s because they were taught differently, or because they are reading it according to their feelings), so they should write defensively. They should generally avoid using the slash or obelus (that is, writing divisions on one line), and instead use the horizontal format with a fraction bar. And when they have to write in-line (such as typing in a comment here) they should use more parentheses than they think they need, such as “(48/3)(2+1)”.
And when they read such an expression, they should be cautious.
Since your perspective is not American, but also not British (as many who insist on juxtaposition-first are), I have to ask: In your contexts, have you ever seen such expressions actually in use? If so, how were they interpreted? I’ve been searching for evidence on that, and rarely found conclusive evidence of actual usage.
Surely, the fact that 2(1+2) is a classic example of the Distributive law, combined with the connection by multiplication between the 2 factors, the division separates the 6 from the 2.
One major problem is that simplifying the parentheses, often stops at 2(3), then they follow PEMDAS for left to right 6/2, then 3*3
Parentheses first
6/2(3) = 6/6 = 1
Perhaps there should be clarification on how to simplify the parentheses. Such as-
Hi, Doug.
As I explained here (and mentioned above), you can’t use the distributive property (a fact about rewriting an expression whose meaning is known) to determine the meaning of the expression.
As for the quotation from Hawkes (section 8 on page 8 in this copy), all he is saying is what we all agree on about parentheses today: that the expression inside is taken as a single entity. He does not say that the entire expression around the parentheses, including the multiplication, must necessarily be treated as a unit.
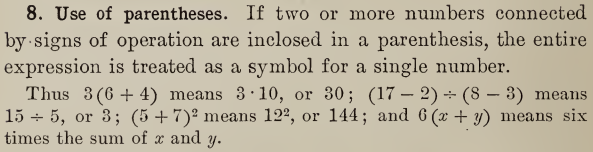
Furthermore, in the next section, he presents the standard PEMDAS rules, with no special mention of implied multiplication:
None of the subsequent examples, in that section or the next, involves the combination of inline division with implied multiplication; all divisions are written with the horizontal bar. As I’ve said, mathematicians avoid the former, with good reason.
Again, my point is not that implied division should or should not be done first, but that we should avoid ambiguity.
I never had this problem at all at school in Scotland for some reason. We weren’t asked such questions that were ambiguous. But engaging with maths tutors and teachers from the USA online they appear to have turned the whole thing into a religion of sorts. “Thou shalt always go left to right and divide comes first”! Of course a great many computer languages also interpret it this way but what is never mentioned (and if I do I get struck down) is to say – put the brackets in and avoid any confusion in the first place! That goes down like a lead balloon since their whole purpose in life is to make basic maths as hard as possible hence justifying their very existence. As a long time academic engineer we never face this problem since we use fractions and brackets where necessary. So just what is the point in all these silly questions? Maths is about communication. Like speech you must be as clear as possible. I would never even write y=1/2x and put it in fractional form just to be sure. If I was programming it I would write it such that y=1/(2x). Also we should not be using the Obelus symbol outside of 4th grade.
I agree with a lot of what you say, but not about teachers. Their goal is to teach whatever they understand to be right, and that is typically either what they learned as children, or what their curriculum says. There is a great deal of inertia in education! And if they believe the rule they were given is right, then they will teach even the hard cases (where they may not really apply), unless they know better.
Now, as I’ve said elsewhere, the books I’ve used generally don’t show any examples of the ambiguous sort of expression, and they do advocate using parentheses for clarity, as well as using the obelus only in restricted applications; but it is clear that there are enough books out there that teach a rigid approach to PEMDAS, to keep it in circulation.
In a comment that was posted to your article about implied multiplication, a reader reasoned the 6÷2(1+2) expression was best described as a word problem this way (paraphrased): that 6 apples were to be distributed/divided among 2 groups of children consisting of three kids each. Considered this way the 6 apples / 2 groups = 3 apples per group or 6 apples / (2 x 3 kids) = 1 apple per kid. So, this gave me the idea to view the expression as a group of sets, to wit: if we describe each group as a set of three distinct items but to further define each set as having 1 boy and two girls that would not change the number of apples per child. You would still have 2 groups of 3 kids each to distribute 6 apples. That could be written as 6 apples / (2 groups x (1 boy + 2 girls)) = 1 apple per kid or…
6 apples / ((2 x 1 boy) + (2 x 2 girls)) = 1 apple per kid. To your point, note the extra set of parentheses but also note the similarity to the actual expression. I really cannot see how one can get 9 apples out of the expression; at least not whole ones!
As I said there to Richard, “the fact that one application of the expression fits your interpretation of the expression is not sufficient to say that the expression must always mean that!” An expression represents a calculation, not a word problem; any given calculation might be used to solve many different problems, and the meaning of a problem is not directly reflected in the way the calculation is written.
We tend to see in an ambiguous expression (or sentence) whatever feels most natural to us at first glance, which is not always what it was intended to mean. It is entirely possible to find a problem for which the correct calculation is to divide 6 by 2 and then multiply by (1+2). Then you will likely want to write it as 6÷2(1+2), even, perhaps, if you believe that implied multiplication should be done first (but definitely if you don’t believe that). For example, suppose that you were told to give 6 apples to every pair of children, and there are one boy and two girls here. Then there are 6/2 apples per child, and (1+2) children, for a total of 6/2(1+2) apples (namely, 9). Of course, if you know thoroughly that in your culture implied multiplication is done first, you would write it as 6/2*(1+2), or as (6/2)(1+2). But you can’t say that no one would write it that way! It’s simply hard for you to imagine, because of what you are accustomed to.
Also, as I’ve said many times, the distributive property is irrelevant to the issue. You can only apply a property after you have decided what the expression, as written, means. When you apply it mechanically, you are making a blind assumption about what to do first.
And I’ll repeat yet again, my argument is not against implied-multiplication-first; it’s against a claim that mathematics requires any particular precedence rule. Grammar is a (communal) choice, not an inherent reality; and the world-wide educational community is not agreed on this choice.
Yes, sir, I get your point, but, gosh, I thought I had perfect descriptions of quotitive (aka quotative) and partitive division. It is hard for me to accept that mathematics does not require any particular precedence rule notwithstanding the need to write unambiguous statements. Does not every body of study especially mathematics and the sciences require foundational knowledge and precepts in order to advance and be understood? I am not so interested in establishing a certain solution to the viral expression but rather that we have a clear set of rules to follow when subject expressions are not ill-defined. I am still disturbed that my college text teaches clearly that a÷bc is a÷(bc) or a over bc yet we have many who see it as (a÷b)c. Does this mean that we have to resort to loads of parentheses and brackets? My point is that the rule for how we solve expressions should also extend to real numbers. Thank you for your keen observations.
Yes, we have to resort to parentheses for clarity. As I’ve said (and will say again in an upcoming post), it would be great to have uniform rules, but we can’t make that happen, and even that wouldn’t prevent ambiguity in practice, whichever rule we chose to agree on.
There are three rules I know of. Your textbook, which will be in that post, taught all-multiplications-first, rather than either strict-PEMDAS or implied-multiplication-first; and that option, too, was taught early (see this very post). Here is what I referred to from Cajori:
All languages have ambiguities, because they are spoken or written by humans.
Division is multiplication of the inverse.
Therefore, the answer to that problem must be 12 and no other. As it is the same as 24 * ¼ * 2, then it doesn’t matter which part you do first;
24 * ¼ = 6 then 6 * 2 = 12;
or ¼ * 2 = ½ then 24 * ½ = 12
Hi, Andy.
On the whole I agree with you in this case (\(24\div4\times2\)), where the operations are explicit, and I say so in Order of Operations: Common Misunderstandings.
On the other hand, as explained in this post and the previous one, Order of Operations: Implicit Multiplication?, ultimately the precedence rules can only be determined by consensus, not proved mathematically. Your argument (and mine) supports the common modern consensus, but if everyone chose to do multiplication first (and there is some tendency in that direction, from what I read), we would have to follow, just as we follow some bits of English grammar that we might prefer not to. Then we would have to explain that the divisor in the example is not \(4\), but \(4\times2\): \(24\times\frac{1}{4\times2}\). (No, I wouldn’t like that.)
You have multiplied the 24 by the reciprocal of the factor 4. The factor 4 is being multiplied by the factor 2. Factors multiplied make a single term, therefore you must use the reciprocal of the term 4*2.
In this example, the multiplication is explicit: \(24\div4\times2\).
So you are saying that all multiplications should be done before divisions (what I’ve called AMF), rather than that implied multiplications are done first, but explicit multiplications in order from left to right (IMF)? Some people do say that, but it’s a different issue (and contrary to Hawkes, whom you quoted in another comment above).
Great article. I have written and studied much lately about PEMDAS/Order of Operations in my own blog and have sharpened my understanding on the subject. One of the problems I have is that some of these online “click-bait” pages (particularly on Facebook) tend to equate the obelus with the solidus and the fraction bar (vinculum), which is a fatal flaw in my opinion. The obelus represents a pure division problem, while the fraction bar or solidus indicates the intention of creating a monomial. Some have (mistakenly) said that an expression like 6 ÷ ½ is nothing more than 6 ÷ 1 ÷ 2 without parentheses and insist the answer is 3. But if the fraction is treated as a monomial as it should be, and we multiply by the inverse of the fraction to solve as most of us were taught, the answer is 12.
With respect to juxtaposition, there’s also the issue of dividing by a mixed number, which is a juxtaposed monomial. 6 ÷ 1½ is not treated as 6 ÷ 1 + ½! So if the juxtaposition that implies addition is not disturbed when working that sort of problem, why would juxtaposition that implies multiplication (which has a higher priority than addition) be disturbed in an expression like 6 ÷ 2(1 + 2)?
Scott
I don’t quite agree with you; the obelus and solidus are not “officially” different in meaning, but “colloquially” the latter is thought of more as marking a fraction, and the former as division. As a result, when I want to type an expression containing a fraction (and implicitly treat that fraction as a distinct entity), I will use a solidus (commonly with spaces around it to emphasize that I am seeing it by itself). I don’t think of that as a rule, just as a natural way to say what I want. For the same reason, when I read such an expression, I tend to guess that the writer intended a fraction, though that is not always true. (It’s harder to type “÷” than “/”, since the latter is on the keyboard, so it is common to type “/” to mean division, without making any distinction. Furthermore, the horizontal fraction bar has exactly the same meaning as both the obelus and the solidus; a fraction is a division.)
For example, if I have in mind the formula for the area of a triangle, \(\frac{1}{2}bh\), but am just typing in-line, I will likely start to type “1/2bh”; but then, realizing that is a little ambiguous, I’d instead type either “1/2 bh”, which more clearly suggests the fraction I have in mind, or “(1/2)bh” to make it absolutely clear. If the context is clear enough that any reader would know I am writing the area formula, I would worry less about being misread. And the same is true of reading what someone else has written, especially if it is a student who may not be as aware of ambiguity as I am. But these are not rules, and not everyone necessarily takes it the same way.
Note that this does not necessarily apply when there is a variable present; 1/ab is more likely to be read as \(\frac{1}{ab}\), so if (for some odd reason) I intended \(\frac{1}{a}b\), I would write it as (1/a)b, and not 1/ab or even 1/a b.
You’re not using the term “monomial” in its proper sense; I think what you mean is “a single entity”.
I presume when you say “6 ÷ ½”, you have in mind “6÷1/2”, since what you typed, using a single symbol for 1/2, leaves no doubt as to the meaning. I would say that “6÷1/2” is sufficiently ambiguous (and odd) that it requires clarification, either by writing “6 ÷ 1/2”, using spacing to imply grouping, or explicitly as “6÷(1/2)”.
But all this is informal , not “rules”; as I suggested, it is “colloquial”.
Now, when you bring in mixed numbers, you are going further outside the realm of order of operations. We don’t use mixed numbers in algebraic expressions, precisely because juxtaposition has a different meaning there. Once you know that a mixed number is being used, you know to follow a separate rule, one that is used in arithmetic, not algebra. I wouldn’t extend that rule to algebra.
So, although I probably agree with how you want to read these expressions, I disagree with the idea that that is an absolute rule, and even more that it is provably correct.
I’ve had the pleasure of graduating for two math heavy master degrees. In a country where PEMDAS was not universally taught before the 80s and the switch in high school teaching happened in the 80s. (In the middle of my high school career that is)
I’ve had to read many mathematical papers for my two theses. And I learned very quickly to first read the style guide of the publication and/or scan the paper for well known theorems or lemmas to figure out the order used.
My biggest problem with the teaching today is that PEMDAS is taught as if it is fundamental to math and therefore unchangable. And no one teaches you neither in highschool or universities that this is wrong. You are left to find it out for yourself.
Now people will run into major problems if they have to use certain journals or for example read Richard Feynman’s work to give a somewhat recent example of a work that distinguishes between a ÷ and a / in meaning. They will learn the wrong thing if they don’t catch on quickly.
I know I got a shock when I read my first paper using PEMDAS one month into my first bachelor’s. My high school was one that made the switch late and I had used an different standard for over a decade! And then again when I learned about implicit multiplication precedence in some journals.
It’s good to teach a standard and have new generations use that when and where they can. But even today they should be aware of the existence of other standards, as you’ll be required to use them if you want to get published in certain well regarded journals or even for writing a thesis or dissertation at certain institutions.
And yes, high school teachers should learn to use the formula editor, or better LaTeX, to write unambiguous problems. Writing ambiguous problems assuming PEMDAS is bad teaching and doing your students a disservice.