Minimizing a Function of Two Variables: Multiple Methods

(A new question of the week)

A recent question from a student working beyond what he has learned led to an interesting discussion of alternative methods for solving a minimization problem, both with and without calculus.

The problem

The question came from Kurisada a couple months ago:

f(x, y) = x² – 4xy + 5y² – 4y + 3 has a min value. Find the value of x and y when f(x, y) is minimum.

This is the first time I met this question, and here is my way:

First I made f'(x) = 2x – 4y = 0.     (I’m not sure if I can make it to f(x) while it is actually f(x, y).)

Therefore x = 2y.

Then I input x = 2y to f(x, y) = y² – 4y + 3 = (y – 2)² – 1

Thus min value = -1

y = 2

x = 4

Apparently this student has not done multivariable calculus, but has invented some of its basic concepts, particularly partial derivatives. The method is nonstandard, but correct. Now we need to show why!

Partial derivatives

Doctor Rick replied:

From your parenthetical comment, it appears that you may not have learned about partial derivatives; but what you have done is perfectly valid.

The partial derivative of f(x, y) with respect to x, ∂f/∂x, is what you get when you differentiate while interpreting y as a constant rather than a variable. The minimum of a function of two variables must occur at a point (x, y) such that each partial derivative (with respect to x, and with respect to y) is zero. (Of course there are other possibilities akin to those in calculus of one variable — if the derivative is not defined, etc. They don’t apply here.)

You found the locus of points on which ∂f/∂x = 0, then wrote a function in one variable representing the value of f(x, y) on that locus, and minimized that function. It worked — good job!

Kurisada just hoped that it would be valid to temporarily pretend that y was constant; in effect, this amounted to slicing the surface defined by function f with a plane \(y = k\), and finding the minimum point of the resulting curve. This is what a partial derivative does: it gives the slope of such a curve.

Here is a graph of the surface defined by f (light blue), showing the intersection with the (arbitrarily chosen) plane \(y = 3.5\) (red) and its minimum point, A. The slope of this curve at any point is \(\frac{\partial f}{\partial x}\). M is the absolute minimum we are seeking.

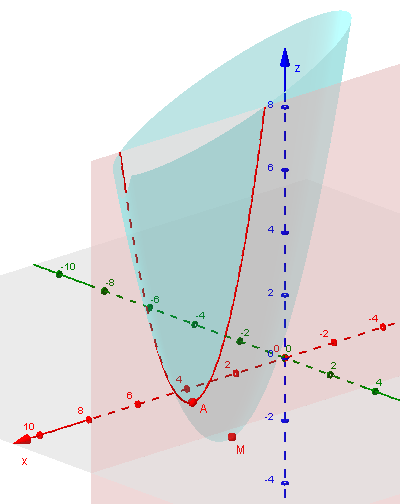
Kurisada had found that the ordered pairs for which \(\frac{\partial f}{\partial x} = 0\) satisfy the equation \(x = 2y\), which is the equation of a plane; so the low points on the y-slices lie on the intersection of this plane with the surface. This curve is the locus (set of points) Doctor Rick referred to. Replacing \(x\) with \(2y\) in the equation \(z = x^2 – 4xy + 5y^2 – 4y + 3\) yielded \(z = (2y)^2 – 4(2y)y + 5y^2 – 4y + 3 = y^2 – 4y + 3\), which is the equation of the projection (“shadow”) of the locus on the yz-plane.

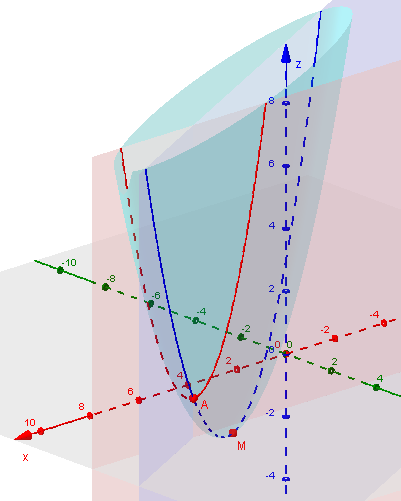
Here I have added in the intersection of the surface with the plane \(x = 2y\) (blue), showing how our point A lies on this locus; M is the minimum point of the locus, and therefore the minimum point on the surface.

The usual calculus method

Kurisada had questions about the reference to each partial derivative:

Is it possible if I regard y as the variable and x as the constant?

Does it mean that actually I need to do both the partial derivatives with respect to x and with respect to y?

Or is it only done to check whether the answer is true?

Doctor Rick replied first to the suggestion to treat only y as the variable:

That should work also. That is, find the locus of points at which ∂f/∂y = 0, then minimize f(x, y) constrained to this locus.

Let’s try that, using Kurisada’s method with y rather than x. We have $$f(x, y) = x^2 – 4xy + 5y^2- 4y + 3,$$ so $$\frac{\partial f}{\partial y} = -4x + 10y – 4,$$ which is zero when $$y = \frac{2x+2}{5}.$$ Putting this into \(f(x,y)\), we get $$f(x, y) = x^2 – 4x\left(\frac{2x+2}{5}\right) + 5\left(\frac{2x+2}{5}\right)^2 – 4\left(\frac{2x+2}{5}\right) + 3.$$ This simplifies to $$\frac{1}{5}(x-4)^2 – 1,$$ whose  minimum again is -1, when \(x = 4\) and \(y = \frac{2(4)+2}{5} = 2.\)

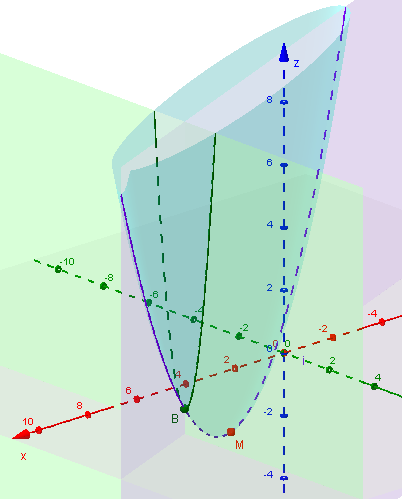
Here we have the intersection of the plane \(x = 7\) (green) with the surface, showing its minimum (B), and the locus of these minima (purple), which again passes through M:

As to whether the method using both partials is needed:

What you did is sufficient. You minimized the function in two directions: the x direction, and along the “valley” you had identified.

My description says that you can also choose to minimize the function in the x and y directions. If you want to try solving the problem this way, use your equation that says ∂f/∂x = 0, and write another that says ∂f/∂y = 0, then solve these two equations simultaneously. This is no more difficult than what you did.

I like this description of the locus of what we might call “east-west” minima as a “valley”; the solution is the lowest point along this valley.

The usual method, as explained here, is to set both partial derivatives to zero, and combine the two resulting equations. The equations, as we’ve seen, are \(2x – 4y = 0\) and \(-4x + 10y – 4 = 0\). Multiplying the first by 2 and adding, we get \(2y – 4 = 0\), giving \(y = 2\); putting this into the first equation, we get \(x = 4\). So the minimum is at \((4, 2)\), and \(f(4, 2) = 4^2 – 4(4)(2) + 5(2)^2 – 4(2) + 3 = -1\) yet again. In effect, here we are finding the intersection of two “valleys” (curves along which we find minima in the east-west and north-south directions).

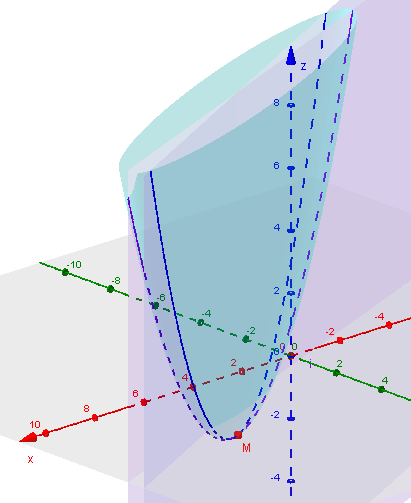
Here is a picture of this method, showing the two loci of minima intersecting at M:

Solving without calculus

Doctor Rick continued, referring to a previous question from Kurisada that specifically asked for multiple ways to solve a problem (an excellent idea!):

Now, in the spirit of your last question, I’ll point out that the problem can also be solved without calculus! We know that a square is minimum when the quantity being squared is zero, since a square can’t be negative. Thus, if you can rewrite the function as a sum of squared quantities and a constant, the minimum will be that constant, and will be attained when each of the squared quantities is zero. See what you can do with this idea!

Kurisada had already done this with \(y^2 – 4y + 3\), and now observed that completing the square on the first two terms “reduced the problem to one already solved”, as we say:

I changed it to (x – 2y)² + y² – 4y + 3

And because (x – 2y)² to make it minimum, it becomes y² – 4y + 3

It is the same to my result! (This way makes me understand more about something I don’t really understand before!)

Doctor Rick finished the work, putting everything together:

Thus far you have changed the function-defining equation

f(x, y) = x² – 4xy + 5y² – 4y + 3

to

f(x, y) = (x – 2y)² + y² – 4y + 3

Now we want to complete the square on the last three terms. But you have already done this! You said in your original posting on this thread that

y² – 4y + 3 = (y – 2)² – 1

That’s exactly what we need. Putting this into the function definition, we get our final result

f(x, y) = (x – 2y)² + (y – 2)² – 1

Now we can see immediately that the least possible value of f(x, y) is –1, attained when both squared quantities are zero, that is, when the following system of equations is satisfied:

x – 2y = 0

y – 2 = 0

The rest is easy.

We have often recommended trying multiple methods as a way to learn math more deeply. As Kurisada mentioned, the non-calculus method helped to see the problem and its answer from a new perspective. I hope my addition of the graphs (made with GeoGebra) adds yet another dimension to your understanding.