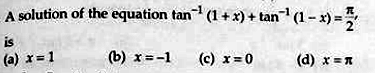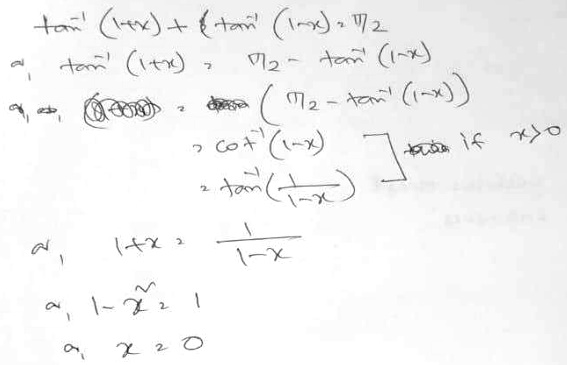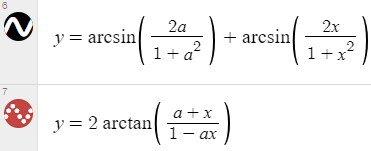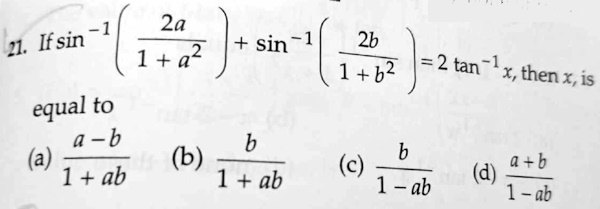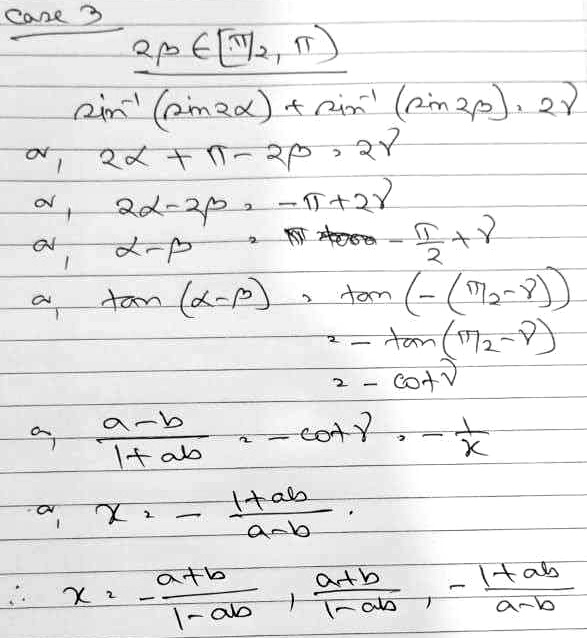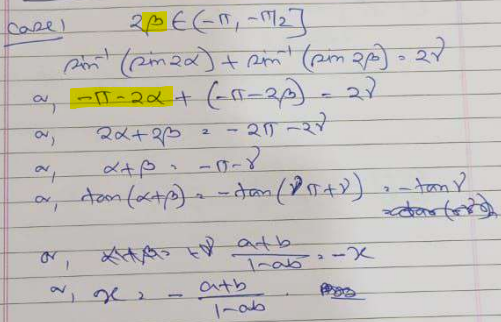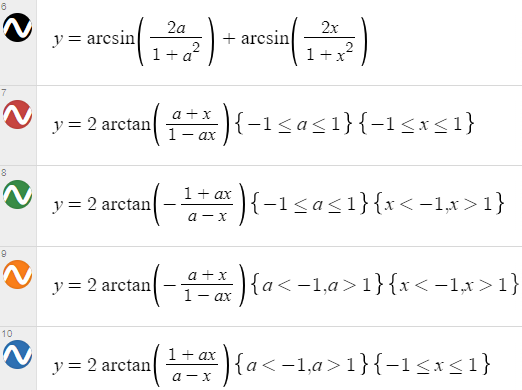Here are a pair of problems related to the last of the three we looked at last time, involving inverse trigonometric function identities with subtle issues. They were probably intended to be rather simple problems (though going beyond what I typically see in American classes) by ignoring the subtleties, but if you approach them as a serious student who cares about details, taking domain or range restrictions into account, you can find yourself in deep water!
First problem: Solving an equation (or not?)
The question came from Debarghya, in early September:
I am getting some questions on inverse trigonometric functions which don’t provide the required domain restrictions and hence using formulae to solve them becomes difficult. For example:
I have attached my solution, but this problem can be solved for x > 0. If x < 0 then tan-1x = cot-1(1/x) – π. Then the solution would be different.
I have seen similar problems in books. Why such questions are asked? … just to check application of simple formulae? … or my understanding is wrong? … Plz help.
Examining the identities
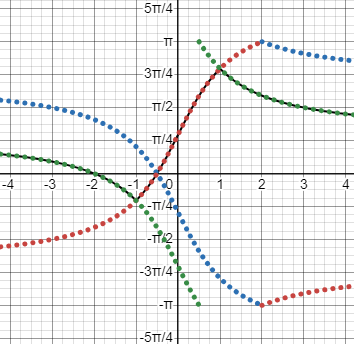
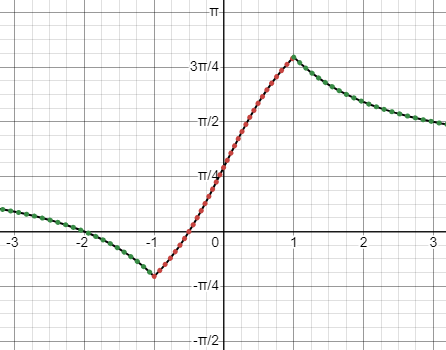
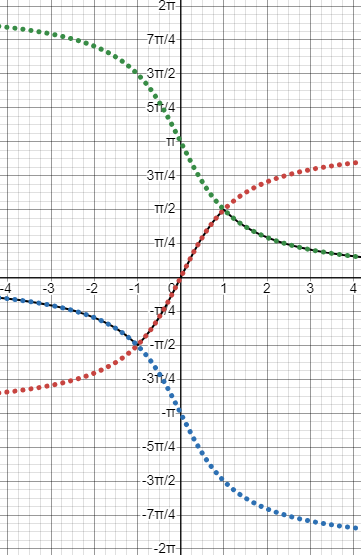
He is aware that various formulas applicable to inverse trig functions are valid only under specified conditions. The first identity he uses, $$\frac{\pi}{2}-\tan^{-1}(u)=\cot^{-1}(u)$$ is always true, because if \(\theta=\tan^{-1}(u)\), so that \(\tan(\theta)=u\) and \(-\frac{\pi}{2}<\theta<\frac{\pi}{2}\), then \(\cot(\frac{\pi}{2}-\theta)=\tan(\theta)=u\) and \(0<\frac{\pi}{2}-\theta<\pi\), so the ranges agree.
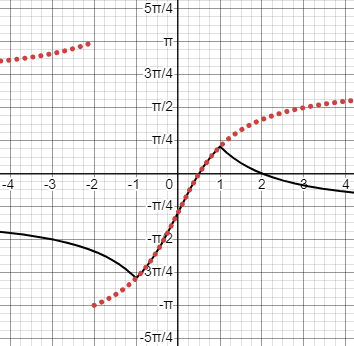
To illustrate, here are the graphs of \(\tan^{-1}(u)\), in red, and \(\frac{\pi}{2}-\tan^{-1}(u)=\cot^{-1}(u)\) in green:
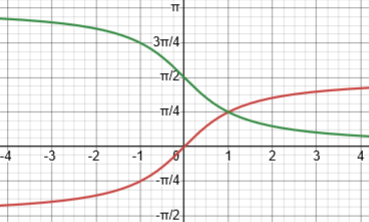
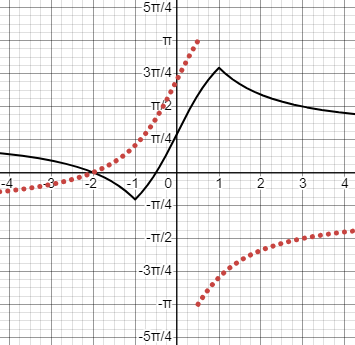
On the other hand, the second “identity”, $$\cot^{-1}(u)=\tan^{-1}(\frac{1}{u})$$ is true only for \(u\ge0\), because the ranges of the two functions don’t match. For positive u, both lie in \((0,\frac{\pi}{2})\); but for negative u, \(\cot^{-1}(u)\) is in \((\frac{\pi}{2}.\pi)\), while \(\tan^{-1}(\frac{1}{u})\) is in \((-\frac{\pi}{2},0)\).
Here are the graphs of \(\cot^{-1}(u)\) in green, and \(\tan^{-1}(\frac{1}{u})\) in red:
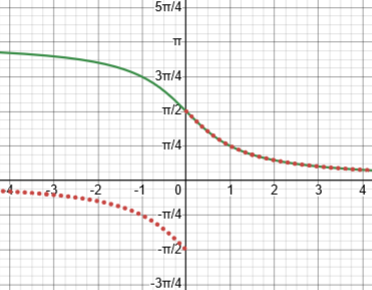
For negative x, we need to add \(\pi\) to the arctan.
One little error in his work is that this means \(\cot^{-1}(1-x)=\tan^{-1}(\frac{1}{1-x})\) only for \(1-x\ge0\), that is, \(x\le1\), not \(x\ge0\). In any case, he has the solution, but without considering all possibilities.
Completing the solution
I answered with a solution taking two cases into account:
I would do something like this:
For all x, π/2 – arctan(1-x) = arccot(1-x), so the equation becomes
arctan(1+x) = arccot(1-x).
Now we have two cases:
- For 1 – x ≥ 0 (that is, x ≤ 1), arccot(1-x) = arctan(1/(1-x)), so the equation becomes
arctan(1+x) = arctan(1/(1-x));
since the arctan function is one-to-one, 1+x = 1/(1-x), from which we find that x = 0.
- For 1 – x < 0 (that is, x > 1), arccot(1-x) > π/2 while arctan(1+x) < π/2, so there can be no solution.
The only solution therefore is x = 0.
(Note, by the way, that it is the sign of 1-x, not of x, that you should have mentioned!)
The last line is the correction I mentioned above.
As to why such questions are asked …
They are asked so that you will learn to handle tricky cases!
(Actually, I don’t see such problems in my face-to-face tutoring work; courses here don’t emphasize inverse trig equations at all. You are just lucky.)
“Lucky”, of course, if you like challenges! As I’ve mentioned, I don’t see a lot of problems about inverse trig functions at all. And now that I’ve thought more about it, I think this was asked not because it was tricky, but because they didn’t notice it was tricky! Keep reading …
What is it really asking?
Doctor Rick had noticed something I’d missed:
Hi, Debarghya, I will add another thought.
The first thing I noticed about the problem is that it says, “A solution,” not “The solution” (or “The solution set“). All we need to do to solve it is to check each option to see if it is a solution. This is easy, requiring only very basic knowledge of the inverse tangent function. Of course, you don’t learn much by solving it this way. We don’t much care for this solution method, in part because real-world math, whether theoretical or practical, doesn’t work this way.
Depending on where the problem came from, it’s possible that the problem creator had in mind less thoughtful students than you, and didn’t even think about the complications that arise when you do the problem “the hard way”!
Very likely, the intent of the problem was just to solve in the simple case, finding a solution and stopping there because that is all we need; but a serious student will not be satisfied with assuming that a multiple-choice problem has only one valid answer, and does not exclude others. This sort of problem – a trap for the wary, rather than for the unwary – is a pet peeve of mine, because it wastes the time of good students, while failing to teach those who don’t care.
Debarghya responded:
Actually dr. this problem along with few such more come from a preliminary book for Indian class 12 exam. I did not think that the problems require critical thinking, but the way you saw this problem is new to me. I am trying to solve other problems in that line of thinking i.e., considering separate cases. If that does not help then I will again ask you….because that is a very interesting logic behind finding the solution.
Checking the option is another way…but I will do that if I cannot solve in proper way.
Thanks again dr..
We’ll see cases galore in the next problem!
Second problem: Simplifying an expression
Then Debarghya asked about a new problem:
I have solved few problems in the same line of thinking…now I am stuck to another problem. I am showing my solution. In fact when I checked over internet I have seen that everywhere a specific condition is assumed as done in the problem mentioned in previous post. Plz see the solution and suggest better way (if any)…
I didn’t initially follow the cases here; if it helps you follow it, we start with the case “When \(|a|\le1\) … ” with subcases “case 1: \(|b|\le1\) … case 2: \(b>1\) … case 3: \(b<-1\) … “. We should expect additional cases \(a>1\) and \(a<-1\), but they are not here.
Ten minutes later, Debarghya showed a second solution without cases:
I have found another shorter way. Plz check if there is any logical error.
Both methods yield the same answer (d), \(x=\frac{a+b}{1-ab}\), but leave gaps.
Is the problem valid?
I answered:
Here is the problem:
If \(\displaystyle\sin^{-1}\frac{2a}{1+a^2}+\sin^{-1}\frac{2b}{1+b^2}=2\tan^{-1}(x)\), then \(x=\)
(a) \(\displaystyle\frac{a-b}{1+ab}\) (b) \(\displaystyle\frac{b}{1+ab}\) (c) \(\displaystyle\frac{b}{1-ab}\) (d) \(\displaystyle\frac{a+b}{1-ab}\)
Is that exactly what it says, with no restrictions on a and b?
If the claim is that one of these answers is correct for all a and b, then the problem is incorrect:
Rather than start by looking for possible errors in your work (which looks good, but the first is complicated by awkward cases, and the second fails to consider different cases at all), I checked the problem itself by graphing.
Taking a to be a constant and b to be x, I graphed
These should agree for all x (and for any a) if your answer is correct.
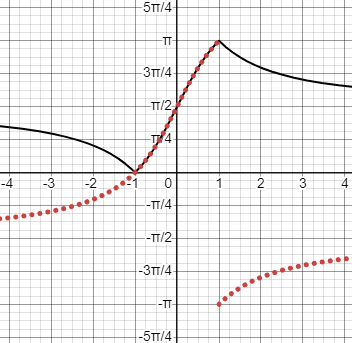
Here is the result (for a = 1):
So for a=1, your answer is correct only for b between -1 and 1.
This shows that for some values of a, his answer is correct only for some values of b, How about other values of a?
Here is the graph when a = -0.5:
It’s still true under the same conditions.
But here it is when a=2:
It’s never correct!
That’s unpleasant …
It looks like the answer (not only yours, but theirs!) is true when both |a| and |b| are less than 1, or something like that.
I haven’t looked further, because I want to know if you left out such a condition. Then we could look for a complete proof.
It looks like this may be another problem where they don’t expect you to think so deeply.
The first problem evidently wasn’t meant to be solved generally; this one perhaps has an unstated assumption about the domain of the variables.
Examining the work
Now Doctor Rick joined in again, looking not just at the validity of the problem, but at the work:
Hi, Debarghya. I have been thinking hard about this problem too, supposing that Doctor Peterson might be too busy to get to it. I see that he has responded, but I have been able to dig a little deeper into your work.
Both your solutions omit parts that would have helped me follow your thinking. For one thing, you pull this identity out of thin air:
sin-1(2a/(1+a2)) = 2 tan-1(a) [1]
Is this common knowledge in your math education? It is new to me.
Debarghya states this only in the case \(|a|\le1\).
For another thing, in your first proof, you didn’t state the reason for taking cases a < -1, -1 ≤ a ≤ 1, a > 1. But I’ll get to that.
I see that equation [1] is (more or less) equivalent to
sin(2x) = 2 tan(x)/(1+tan2(x)) [2]
which is also new (and interesting!) to me; I had to prove it for myself. But exploring further regarding the “more or less” I inserted above (namely, the usual need to check ranges of inverse trig functions), I find that equation [1] is only true for -1 ≤ x ≤ 1. At this point I see why you needed to consider cases in your first solution.
We saw last time that \(\sin(2\theta)=\frac{2\tan(\theta)}{1+\tan^2(\theta)}\), which was new to me in mid-August from elsewhere. We’ll see something about the restriction as we continue. [I think.]
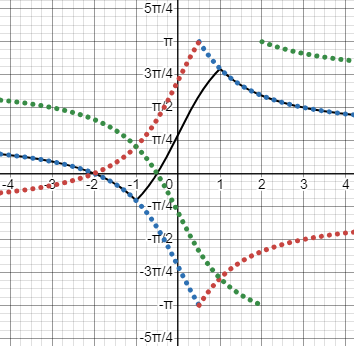
For other cases, Debarghya mentioned that for \(b>1\), $$\sin^{-1}\left(\frac{2b}{1+b^2}\right)=\pi-2\tan^{-1}(b)$$
and for \(b<-1\), $$\sin^{-1}\left(\frac{2b}{1+b^2}\right)=-\pi-2\tan^{-1}(b)$$
We can see those three cases here:

Here is how I would start work on the problem. Confronted with the equation
sin-1(2a/(1+a2)) + sin-1(2b/(1+b2)) = 2 tan-1(x) [3]
I first wonder about the domain of each term in the LHS. We know that the domain of sin-1 is [–1, 1], so the first term is defined if and only if
–1 ≤ 2a/(1+a2) ≤ 1 [4]
A little algebra shows that this is true for all a.
One way to see this is that, on one hand, $$\frac{2a}{1+a^2}=\frac{1+2a+a^2}{1+a^2}-1=\frac{(1+a)^2}{1+a^2}-1\ge-1$$ since \(\frac{(1+a)^2}{1+a^2}\ge0\). and, on the other hand, $$\frac{2a}{1+a^2}=1-\frac{1-2a+a^2}{1+a^2}=1-\frac{(1-a)^2}{1+a^2}\le1$$ since \(\frac{(1-a)^2}{1+a^2}\ge0\).
So the entire LHS is defined for all real values of a and b.
Then there’s the matter of the ranges of the inverse trig functions, with which you have been dealing. Here I notice that the range of each term in the LHS of [3] is [-π/2, π/2], so that the range of the entire LHS is [–π, π]. But this is exactly the range of the RHS! Thus I see that for any a and b, half of the LHS will be in the range of tan-1(x), and there is no range issue in this problem.
That is, \(\sin^{-1}\left(\frac{2a}{1+a^2}\right)\) and \(\sin^{-1}\left(\frac{2b}{1+b^2}\right)\) can each (independently) take on any value from \(-\frac{\pi}{2}\) to \(\frac{\pi}{2}\), so that their sum can take on any value from \(-\pi\) to \(\pi\). So the LHS is always a possible value of the RHS, \(\tan^{-1}(x)\).
So the problem at least makes sense.
As we proceed to actually solving the problem, if we introduce equation [1] we have this difficulty that [1] is only true for x in [-1, 1]. Apparently you have more than equation [1]; you have variants for the other cases. Again, this is not something I have seen before.
I showed those other cases above. Now we are up to Debarghya’s level of knowledge on these identities! And although his coverage of cases was incomplete, the general idea of the first solution seems good.
How about the second solution?
Your second solution nicely avoids that issue by using equation [2], which is true for all x, rather than [1] which is not. However, it still has problems. You should state at the start that α, β, and γ are in (–π/2, π/2), the range of both sin-1 and tan-1, then consider the consequences of these restrictions at each step. For example, is it true that sin-1(sin 2α) = 2α for all α in (–π/2, π/2)?
It may be fine to ignore all these issues if you seek a “quick solution” in a timed test; you have found that only option (d) could possibly be correct, and the details won’t change this — they could only cause all options to be incorrect. I know you want to be able to work out problems fully and not take short-cuts like this, and I approve of that determination.
Refining the solution
Debarghya replied:
I have posted the actual question and have solved the problem again considering all cases…plz see…
As before, he has assumed one case for α, and taken the three cases for β; so not all cases have been covered. The three solutions presumably correspond to the cases where, respectively, \(b<-1\), \(|b|\le1\), and \(b>1\). As we’ll see, that doesn’t quite work.
I answered, again just checking rather than focus on the work:
Your answer,
\(x=-\frac{a+b}{1+ab},\frac{a+b}{1-ab},-\frac{1+ab}{a-b}\)
seems to be partly correct, if you specify the domain of each case. But your cases appear to have only taken into account the values of b, and ignored a.
I find that if |a| ≤ 1, then the second and third graphs match (the third for |x| > 1), but the first seems to never fit:
This is for a = 0.5, and is typical when |a| ≤ 1:
So what was claimed to work for \(b<-1\) doesn’t, and what was claimed to work only for \(b>1\) actually works for \(|b|>1\). Why? Because the work for case 1 actually assumed both \(a<-1\) and \(b<-1\), not for this case where \(|a|>1\).
But if |a| ≥ 1, only the first formula (black) works, and not for all b (this is for a = 2):
So in this case, \(a>1\), the first formula applies when \(|b|>1\), and some fourth formula applies when \(|b|<1\).
I think things may work out fully if you make your cases take into account both a and b. I think that there will really be 9 cases, several of which will have the same answer.
As an example, notice that in your case 1,
you are actually assuming that both α and β are in this interval; so this result applies in the left-hand region of my graph only in the second graph, not the first.
But this shows that you are very close to a good solution. (It also shows that the author of the problem did not expect you to be as careful about details as you are!)
Presumably the author intended the student to either assume the easiest case, or to ignore cases entirely.
Debarghya responded:
Yes…Dr I understand your point…for three variables there would be 9 cases similar to the method applied for (2 alpha)…it is true that the author did not mean to solve it for all such cases…it is an elementary book and there are several examples in the book which avoid any case and just apply basic formula straightway… but I tried to solve it from my own curiosity…thanks Dr.
Making a final answer
I did some more experimenting, without trying to write out a complete derivation for each case:
Yes, it seems good to explore how to get this right, even though it is not expected.
For fun, I perfected my Desmos graph, so it works for all a:
For \(a=\frac{1}{2}\):
For \(a=2\):
and so on.
The four cases cover all 9, if you look carefully.
I think the conditions might be able to be simplified a little, but this satisfies me!
We could, indeed, rewrite the solution:
$$\text{If }\sin^{-1}\frac{2a}{1+a^2}+\sin^{-1}\frac{2b}{1+b^2}=2\tan^{-1}(x)\text{, then }\\x=\left\{\begin{matrix}\frac{a+b}{1-ab} & \text{if }|a|\le1\text{ and }|b|\le1 \\-\frac{a+b}{1-ab} & \text{if }|a|\ge1\text{ and }|b|\ge1 \\\frac{1+ab}{a-b} & \text{if }|a|\ge1\text{ and }|b|\le1 \\-\frac{1+ab}{a-b} & \text{if }|a|\le1\text{ and }|b|\ge1 \\\end{matrix}\right.$$
Interestingly, the four possible answers (under different conditions) are choice (d) in the problem, and its arithmetic and/or multiplicative inverse (that is, negated and/or flipped over). None of the other choices is close.
Debarghya replied:
Yes…this is really beautiful…and I have also checked these graphs…thanx dr.
I’ve left the actual proof of all cases for you …