Integration: It Takes a Whole Toolbox

Individual techniques of integration, as discussed in the last two posts, don’t represent the reality of the process, any more than demonstrating how to use a hammer or a screwdriver shows how to do carpentry. Let’s look at two questions we’ve had about challenging integrals that require a combination of methods. We’ll be using substitution, partial fractions, parts, and other methods, including trigonometric identities.

Integrating by parts twice … or not

This 2008 question ends up with a little twist:

Integration by Parts

I'm trying to integrate e^x(x+1)/(x+2)^2 and am stuck.  I tried
letting x+2 = t with 1 = dt/dx but didn't get anywhere.  Can you help me?

It’s a reasonable substitution; if we try it, we get

$$\int\frac{e^x(x+1)}{(x+2)^2}dx=\int\frac{e^{t-2}(t-1)}{t^2}dt$$

which might help a little, by making the denominator simpler, so we can, for example, split the fraction into a sum (in fact, it’s quite a nice start), but doesn’t get us very far by itself.

To my eye, since we have algebraic and exponential factors, integration by parts seems likely; but the algebraic part doesn’t invite us to either differentiate or antidifferentiate it! What can we do?

Doctor Ali took this one, just getting it started:

Hi Arpita!

Thanks for writing to Dr. Math.  Here's how I'd approach it:

    -
   |    x+1       x
   | --------- * e  dx
   |  (x+2)^2
  -

Write it this way in order to expand the numerator:

    -
   |   x+2-1      x
   | --------- * e  dx
   |  (x+2)^2
  -

Break the fraction into two separate fractions:

    -              -
   |   e^x        |    e^x
   | ------- dx - | --------- dx
   |  (x+2)       |  (x+2)^2
  -              -

This is the technique I called “partial cancellation” a couple weeks ago; splitting into a sum this way is just what I would have done next after the substitution above. So far, we have

$$\int\frac{e^x(x+1)}{(x+2)^2}dx=\int\frac{(x+2)-1}{(x+2)^2}e^xdx\\=\int\left(\frac{x+2}{(x+2)^2}e^x-\frac{1}{(x+2)^2}e^x\right)dx=\int\frac{e^x}{x+2}dx-\int\frac{e^x}{(x+2)^2}dx$$

Let the first integral be as it is.

I’m not [initially!] sure what he means here, as there is work to do for this integral; we’ll do it below, and see why he sets it aside.

Use integration by parts to integrate the second one.  We take 

  dv = dx/(x+2)^2

We do this way because we know the integral of dv:

          1
  v = - -----
         x+2

Use the main formula of integration by parts:

    -             -
   |  udv = uv - |  vdu
  -             -

Can you continue the process yourself?

Now, 16 years later, we may as well try to finish.

Taking \(u=e^x\) and \(dv=\frac{1}{(x+2)^2}dx\), we have \(du=e^xdx\) and \(v=\frac{-1}{x+2}\), and

$$\int \underset{u}{\underbrace{e^x\strut}}\underset{dv}{\underbrace{\frac{1}{(x+2)^2}dx}}=\underset{u}{\underbrace{e^x\strut}}\underset{v}{\underbrace{\frac{-1}{x+2}}}-\int\underset{v}{\underbrace{\frac{-1}{x+2}}}\underset{du}{\underbrace{e^xdx\strut}}\\=\frac{-e^x}{x+2}+\int\frac{e^x}{x+2}dx$$

Here we took the algebraic part (the fraction) as \(dv\) because integrating it would make it simpler; it doesn’t matter where we put \(e^x\). And now we are left with another copy of that first integral we set aside!

So we repeat the process, and use parts for this integral; but here we run into a problem (quite possibly what Arpita found). If we take \(u=e^x\) and \(dv=\frac{1}{x+2}dx\), then \(du=e^xdx\) and \(v=\ln(x+2)\), so we have

$$\int \underset{u}{\underbrace{e^x\strut}}\underset{dv}{\underbrace{\frac{1}{x+2}dx}}=\underset{u}{\underbrace{e^x\strut}}\underset{v}{\underbrace{\ln(x+2)}}-\int\underset{v}{\underbrace{\ln(x+2)}}\underset{du}{\underbrace{e^xdx\strut}}=e^x\ln(x+2)-\int e^x\ln(x+2)dx$$ That doesn’t look like an improvement.

But if we take \(u=\frac{1}{x+2}\) and \(dv=e^xdx\), then \(du=\frac{-1}{(x+2)^2}dx\) and \(v=e^x\), so we have

$$\int \underset{u}{\underbrace{\frac{1}{x+2}}}\underset{dv}{\underbrace{e^xdx\strut}}=\underset{u}{\underbrace{\frac{1}{x+2}}}\underset{v}{\underbrace{e^x\strut}}-\int\underset{v}{\underbrace{e^x\strut}}\underset{du}{\underbrace{\frac{-1}{(x+2)^2}dx}}=\frac{e^x}{x+2}+\int\frac{e^x}{(x+2)^2}dx$$ bringing us back where we started.

But wait!

Putting the pieces together without doing that integral, we have

$$\int\frac{e^x(x+1)}{(x+2)^2}dx=\int\frac{e^x}{x+2}dx-\int\frac{e^x}{(x+2)^2}dx\\=\int\frac{e^x}{x+2}dx-\left(\frac{-e^x}{x+2}+\int\frac{e^x}{x+2}dx\right)\\=\int\frac{e^x}{x+2}dx+\frac{e^x}{x+2}-\int\frac{e^x}{x+2}dx=\frac{e^x}{x+2}$$

Interesting: We don’t really have to evaluate that first integral after all, since it cancels out! Now we know why Doctor Ali just set it aside. (In fact, if I ask Wolfram Alpha to integrate the first integral, it gives an answer in terms of something called “the exponential integral Ei”, which means this can’t be integrated in terms of elementary functions.)

Trig and partial fractions

Two days later, Ali answered another one:

Challenging Trig Expression Integration

For the life of me, I can't figure out how to integrate this function:

         (sin x)^3
  -----------------------
  [(sin x)^3]+[(cos x)^3]

There is no convenient form that this can take so that substitution, integration by parts, or both can be performed. I've looked in several textbooks and online sites and haven't seen anything remotely close to this, but the answer is exact and symbolic (no Taylor series needed).

  answer:(x/2) - (1/6)ln(cos x + sin x) + (1/3)ln(2 - sin(2x))

I've tried a huge number of different trig identities to force this into a form which is integrable by substitution or by parts (probably need both). I also completed the square on several of them to make two pieces that are perhaps then able to be converted to integrable forms. Nothing works. I got the answer from Wolfram Integrator. I've commonly found that it can be misleading because a more human approach will produce an equivalent form that isn't necessarily obvious that it matches Wolfram's answer. 

The first part, (x/2), bothers me because every integration I've performed with trig functions produces a trig function or an exponential. So I used that as my starting point to try and figure out how that can even come about from a trig function, but so far I've gotten nowhere with that.  Maybe this needs to be performed in complex or hypergeometric?

Wolfram Alpha gives essentially the same answer today.

There are some good ideas here (including the recognition that the answer he gets may look very different from what software produces). But also, it’s dangerous to “reverse-engineer” a solution! That linear term is not central to the answer, but incidental, as we’ll see.

Unfortunately, Ryan has missed one method: partial fractions! We’ll start, though, with some trig identities.

Doctor Ali said:

Hi Ryan!

Thanks for writing to Dr. Math.  It sounds like you've done a lot of good thinking so far.  I think the trick to this is doing some algebraic manipulation.  I'd start it this way:

    -
   |        sin(x)^3
   | --------------------- dx
   |  sin(x)^3 + cos(x)^3
  -

Divide the top and bottom by cos(x)^3:

    -
   |    tan(x)^3
   | -------------- dx
   |  tan(x)^3 + 1 
  -

$$\int\frac{\sin^3(x)}{\sin^3(x)+\cos^3(x)}dx=\int\frac{\frac{\sin^3(x)}{\cos^3(x)}}{\frac{\sin^3(x)}{\cos^3(x)}+\frac{\cos^3(x)}{\cos^3(x)}}dx=\int\frac{\tan^3(x)}{\tan^3(x)+1}dx$$

I often prefer to write an expression in terms of sine and cosine, rather than the reverse; but sometimes you just have to try everything to find something that works. At least here we have only one trig function!

Now we can try a substitution using the obvious “inner” function, the tangent, and work out the differential using an identity:

Assume TAN(x) = u, so (1 + tan(x)^2) dx = du

    -
   |         u^3
   | ------------------- du
   |  (u^3 + 1)(u^2 + 1)
  -

Does that make sense?

Here are the details: Letting \(u=\tan(x)\), \(du=\sec^2(x)dx=(1+\tan^2(x))dx\), and therefore $$dx=\frac{du}{1+\tan^2(x)}=\frac{du}{1+u^2}$$ This gives

$$\int\frac{\tan^3(x)}{\tan^3(x)+1}dx=\int\frac{u^3}{u^3+1}\frac{dx}{u^2+1}$$

Now we have a rational function, which we can always integrate by partial fractions.

Let's try to break that fraction into an equivalent sum of fractions.  This is the key algebraic step I referred to above:

    -
   | /     2u - 1         u - 1         1     \
   | |--------------- - ---------- - -------- | du
   | \ 3(u^2 - u + 1)   2(u^2 + 1)   6(u + 1) /
  -

Can you do this yourself?

This way, we change the difficult integral to three not so difficult integrals.

Here’s one version of the work to obtain this. We first factor the sum of cubes:

$$\frac{u^3}{(u^3+1)(u^2+1)}=\frac{u^3}{(u+1)(u^2-u+1)(u^2+1)}$$

Now we want

$$\frac{u^3}{(u^2-u+1)(u^2+1)(u+1)}=\frac{Au+B}{u^2-u+1}+\frac{Cu+D}{u^2+1}+\frac{E}{u+1}$$

Solving this, I get $$A=\frac{2}{3},B=-\frac{1}{3},C=-\frac{1}{2},D=\frac{1}{2},E=-\frac{1}{6}$$

So we have $$\frac{u^3}{(u^2-u+1)(u^2+1)(u+1)}=\frac{2u-1}{3(u^2-u+1)}+\frac{-u+1}{2(u^2+1)}+\frac{-1}{6(u+1)}$$

Now we have to integrate the sum, using these hints:

Hints:

1) The first integral can be solved using LN, because the top is a multiple of the bottom's derivative.

2) The second integral splits to give one LN and one ARCTAN.

3) The third integral is a simple LN.

Can you continue the solution yourself?  By the way, don't forget to substitute TAN(x) back for u at the end.

In his order, we have $$\int\left[\frac{2u-1}{3(u^2-u+1)}-\frac{u-1}{2(u^2+1)}-\frac{1}{6(u+1)}\right]du$$

I’ll take one term at a time.

Part 1: The numerator is just the derivative we need, so let \(v=u^2-u+1\) and \(dv=(2u-1)du\):

$$\frac{1}{3}\int\frac{2u-1}{u^2-u+1}=\frac{1}{3}\int\frac{dv}{v}=\frac{1}{3}\ln|v|=\frac{1}{3}\ln\left|u^2-u+1\right|=\frac{1}{3}\ln\left|\tan^2(x)-\tan(x)+1\right|$$

Part 2: If \(v=u^2+1\), then \(dv=2udu\), so we split into two integrals:

$$-\frac{1}{2}\int\frac{u-1}{u^2+1}du=-\frac{1}{2}\int\frac{udu}{u^2+1}+\frac{1}{2}\int\frac{du}{u^2+1}$$

Part 2a: Let \(v=u^2+1\), and \(dv=2udu\): $$-\frac{1}{4}\int\frac{2udu}{u^2+1}=-\frac{1}{4}\int\frac{dv}{v}=-\frac{1}{4}\ln|v|=-\frac{1}{4}\ln\left|u^2+1\right|=-\frac{1}{4}\ln\left|\tan^2(x)+1\right|$$

Part 2b: $$\frac{1}{2}\int\frac{du}{u^2+1}=\frac{1}{2}\arctan(u)=\frac{1}{2}x$$

Aha! We found the source of the linear term that baffled Ryan.

Part 3: Here we can use a substitution so simple I would not explicitly define the new variable, but would do it all in my head. Let \(v=u+1\), so \(dv=du\):

$$-\frac{1}{6}\int\frac{du}{u+1}=-\frac{1}{6}\int\frac{dv}{v}=-\frac{1}{6}\ln|v|=-\frac{1}{6}\ln|u+1|=-\frac{1}{6}\ln|\tan(x)+1|$$

Putting it together, our solution is $$\frac{1}{3}\ln\left|\tan^2(x)-\tan(x)+1\right|-\frac{1}{4}\ln\left|\tan^2(x)+1\right|+\frac{1}{2}x-\frac{1}{6}\ln|\tan(x)+1|+C$$

Reconciling our answer

But we expected to get $$\frac{1}{3}\ln\left|2-\sin(2x)\right|-\frac{1}{6}\ln|\cos(x)+\sin(x)|+\frac{1}{2}x+C$$

Our answer looks entirely different; but when I graph these two solutions together, I find that they differ by a constant, about 0.23.

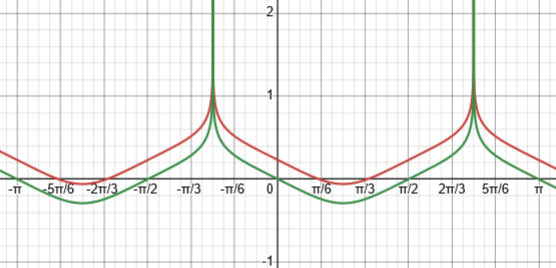
So our answer appears to be correct.

But when I graph the three non-linear terms of our solution individually (broken), none of them agrees with either of the two non-linear terms of the computer solution (solid):

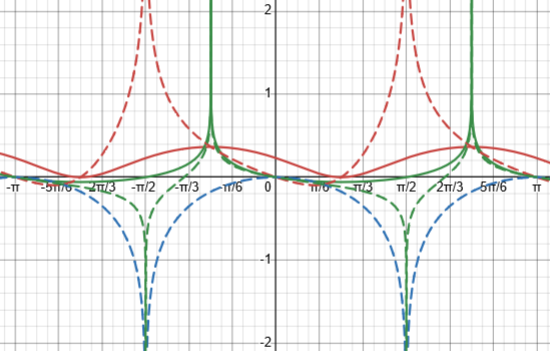
The first thing I think of to rewrite the computer answer is to express it in terms of trig functions of x only, by changing \(\frac{1}{3}\ln\left|2-\sin(2x)\right|\) to $$\frac{1}{3}\ln\left|2(1-\sin(x)\cos(x))\right|=\frac{1}{3}\ln2+\frac{1}{3}\ln\left|1-\sin(x)\cos(x)\right|.$$ And lo and behold, \(\frac{1}{3}\ln2\approx0.231\)! That explains the constant difference (which is absorbed into the arbitrary constant). So we’d like to show that our solution is equal to this: $$\frac{1}{3}\ln\left|1-\sin(x)\cos(x)\right|-\frac{1}{6}\ln|\cos(x)+\sin(x)|+\frac{1}{2}x+C$$

Let’s take our three terms one by one, and try to express them in terms of the arguments in the desired solution:

Part 1: $$\frac{1}{3}\ln\left|\tan^2(x)-\tan(x)+1\right|\\=\frac{1}{3}\ln\left|\sec^2(x)-\tan(x)\right|$$

$$=\frac{1}{3}\ln\left|\frac{1-\sin(x)\cos(x)}{\cos^2(x)}\right|\\=\frac{1}{3}\ln\left|1-\sin(x)\cos(x)\right|-\frac{1}{3}\ln\left|\cos^2(x)\right|$$

$$=\frac{1}{3}\ln\left|1-\sin(x)\cos(x)\right|-\frac{2}{3}\ln\left|\cos(x)\right|$$

Part 2a: $$-\frac{1}{4}\ln\left|\tan^2(x)+1\right|=-\frac{1}{4}\ln\left|\sec^2(x)\right|$$

$$=-\frac{1}{4}\ln\left|\frac{1}{\sec^2(x)}\right|=\frac{1}{4}\ln\left|\cos^2(x)\right|$$

$$=\frac{1}{2}\ln\left|\cos(x)\right|$$

Part 3: $$-\frac{1}{6}\ln|\tan(x)+1|\\=-\frac{1}{6}\ln|\frac{\cos(x)(\tan(x)+1)}{\cos(x)}|\\=-\frac{1}{6}\ln|\cos(x)(\tan(x)+1)|+\frac{1}{6}\ln|\cos(x)|\\=-\frac{1}{6}\ln|\sin(x)+\cos(x))|+\frac{1}{6}\ln|\cos(x)|$$

Adding these up, together with part 2b, a piece of each cancels out, and we get $$\frac{1}{3}\ln\left|1-\sin(x)\cos(x)\right|{\color{Red}{-\frac{2}{3}\ln\left|\cos(x)\right|}}\\{\color{Red}{+\frac{1}{2}\ln\left|\cos(x)\right|}}+\frac{1}{2}x\\-\frac{1}{6}\ln|\sin(x)+\cos(x))|{\color{Red}{+\frac{1}{6}\ln|\cos(x)|}}\\=\frac{1}{3}\ln\left|1-\sin(x)\cos(x)\right|+\frac{1}{2}x-\frac{1}{6}\ln|\sin(x)+\cos(x))|+C$$

And this is what we wanted!

Again, we didn’t have to do all this, but it’s fun to see it all come together. Computer systems do things differently than humans, and often come up with oddly different results.