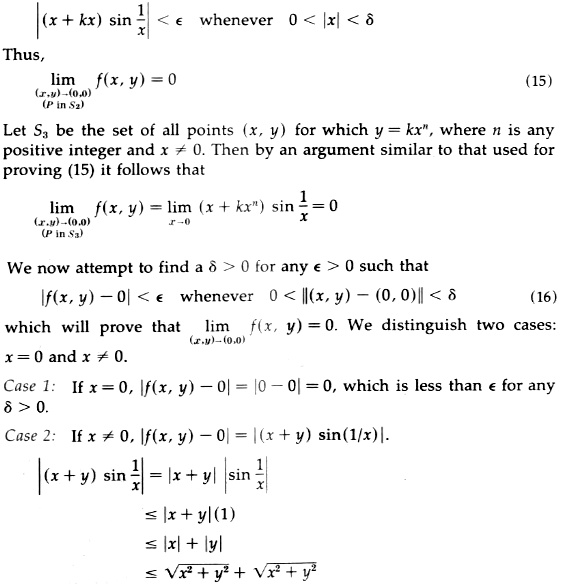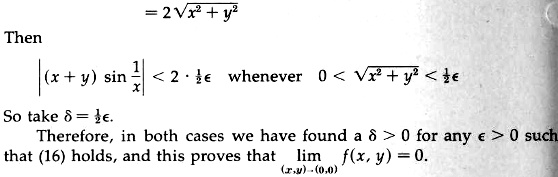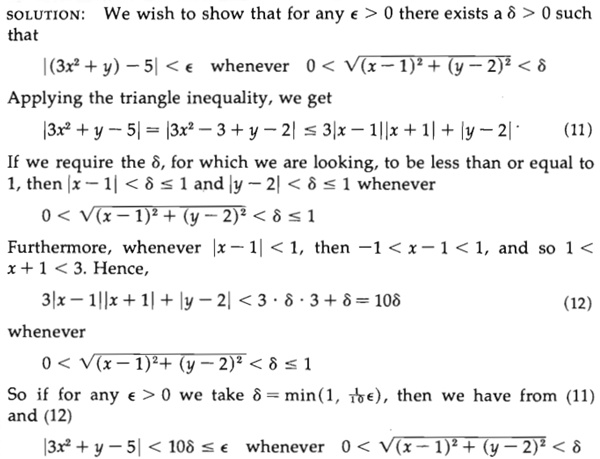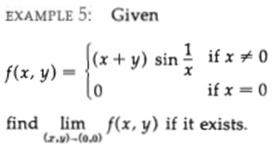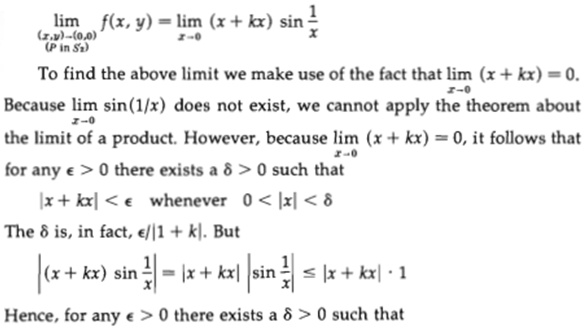Last time, we looked a little more deeply than usual at an epsilon-delta proof of a simple function of one variable. Here, we have two questions about such proofs for a function of two variables, to illustrate how you can question aspects of such a proof and satisfy yourself that it is valid – or fill in gaps.
I will not cover this topic completely; I just want to focus on how to ask and answer your own questions about a proof. As far as we need to go, the definition is essentially the same as for one independent variable.
Question 1: Why not just less than?
The questions came from Kalyan at the start of March. I’m splitting the one question about two different items from a book into two separate discussions for readability.
The book is Leithold’s The Calculus, with Analytic Geometry, from 1976.
Here is Definition 19.2.5, which will be referred to:
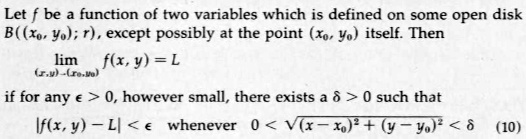
Here is the first question, about a limit proof very similar to the one from last time.
Hello Doctor,
1) For the below snippet:
Why have they taken δ ≤ 1, why not just δ < 1? As we did for limits in a function in one variable for which I spent months to get through (somehow).
Regards
The question is about that line, “If we require the δ. for which we are looking, to be less than or equal to 1, …” This is very similar to one of the issues last time, but more specific.
I answered:
When you want to know why the author didn’t do this other thing, try doing that other thing and see what happens! In particular, look for where in the proof that fact is used.
But ultimately, as we’ve seen elsewhere, this sort of thing is an arbitrary choice. The main goal is merely to keep delta from being too large and affecting the other things you are doing. We often use 1, rather than, say, 2 or 73, because it’s a nice number. And for the same reason, it doesn’t really matter whether we say < or ≤ .
On the other hand, I do see a place in the proof where it turns out to be very convenient to use ≤ .
Hint: look at “δ = min(1, ε/10)”. On what grounds can he write that? What would happen if he used δ < 1?
(I imagine that δ ≤ 1 has been used before, somewhere in single variables. You just forgot.)
Note that I asked two separate questions here: First, why is it correct to write what he did; and second, how would the subsequent work be different if you changed it to what you expected?
It’s good to ask yourself why a step in a proof is needed, to sharpen your own reasoning skills; but figuring that out for yourself is even better. That’s why we push students to do that.
Asking whether it could have been done differently, or how the author might have thought of that step, is a further matter to be dealt with after you understand what was done.
Kalyan replied:
Since the day I have encountered Epsilon-Delta the first time, I have one question in mind, that is why I always feel skeptical about my attempts which results in avoiding this topic altogether. However, I have to learn it as it is one of the most beautiful and useful topics of calculus.
When you said to try. Then, what I should do? I am not at all aware, or somewhat unaware, on how to start.
If I take that δ < (say, 1). Then, I choose ε, then find the corresponding δ and after multiple attempts it is certain that as ε comes closer the delta also gets closer however small.
Coming to the question asked:
On what grounds can he write that? What would happen if he used δ < 1?
If δ < 1 , then choosing the minimum of (1 or ε/5) would not be possible, and it will difficult to judge which of the two numbers need to be taken minimum, which will complicate the calculations.
He may have part of the right thought here; but he has skipped over my first question, about the role of the minimum, by starting with the question of δ < 1.
I responded:
No, I wouldn’t say that it would not be possible. It’s always possible to find the smaller of two numbers!
Please try again, thinking about the overall logic.
If we have shown that certain things are true as long as δ ≤ 1, and one of those things is that as long as a certain quantity is less than ε/10, we have a limit, then why can we conclude that taking δ = min(1, ε/10) will work? What is the significance of the minimum there? That’s my first question.
The second question, what changes if you only required δ < 1 in the earlier part of the proof, can be considered after we answer the first.
(By the way, this question of mine does not require fully understanding the epsilon-delta concept; I’m trying to narrow things down for you, helping you focus on one thing at a time.)
Focusing on one detail at a time (after a first quick read-through to see the general flow) is helpful.
After some discussion, I eventually stated what I had in mind:
As I said,
If we have shown that certain things are true as long as δ ≤ 1,
and one of those things is that as long as a certain quantity is less than ε/10, we have a limit,
then why can we conclude that taking δ = min(1, ε/10) will work?
What is the significance of the minimum there?
Let’s follow the logic.
He showed that if δ ≤ 1, then it will be true that
|3x2+y-5| < 10δ whenever 0 < √((x-1)2 + (y-2)2) < δ
So if we take δ (for a given ε) to be min(1, ε/10), then [here is the answer I’m looking for!]
we know that δ, being the minimum of those two numbers, is less than or equal to both 1 and ε/10.
(We could state this as a theorem: If x = min(a, b), then x ≤ a and x ≤ b.)
That means that, on one hand,
δ ≤ 1,
so that everything that was worked out previously (based on that assumption) is valid, and, on the other hand,
|3x2 + y – 5| < 10δ ≤ 10 ε/10 = ε
so that we have a limit.
We needed δ to be no greater than both of those numbers, so we made it so by using the minimum.
That’s why using the minimum works. Do you follow that logic? It’s common to many epsilon-delta proofs.
That’s why we use the minimum; how does that help answer the original question?
Now, what if we had assumed at the start of that reasoning that δ < 1, which seems stronger, and more natural, than ≤? We’d find, when we wanted to use the minimum, that what I just described didn’t quite work! The minimum is ≤ each of the values, not < each of them! That is, we couldn’t say that if δ = min(1, ε/10), then δ < 1 (because it might be equal to 1), so we couldn’t say that all the work before that was valid.
Now, it’s not hard to fix that; we might have taken δ = min(1/2, ε/10), so that δ ≤ 1/2 < 1. But it’s easier just to start out with δ ≤ 1 in the reasoning, which, being arbitrary, doesn’t break anything.
Do you follow this?
In reading the proof, if we had the question “Why assume δ ≤ 1?” in our mind, when we reach the mention of the minimum, and think carefully about why that does what we need, we might also see that this answers our question.
Do you also see that we didn’t really have to think about the reason for “≤” in order to follow the proof? He made an arbitrary choice, informed by his knowledge of how the proof would proceed (and perhaps either having written a preliminary proof with a different choice, and improved it before putting it in the book, or just seen such a proof elsewhere and used what he knew would work nicely).
On the other hand, once we understand how the proof works as given, it can be useful for our own deeper understanding of the process of proving, to ask these questions of “why might he have chosen to do it this way rather than what seems more natural to me?”. In fact, we have perhaps learned a few things in working through this.
My key point is that this level of thinking comes after understanding what is actually being said. That’s why I wanted you to think through the precise role played by the minimum.
Next, he had a very good question about an example problem that again uses the epsilon-delta definition of a limit.
Question 2: Why did he ignore a special case?
Read carefully through the solution to this problem, and see if you notice what’s wrong. It’s a good exercise:
2)
…
Here, the author has not taken k = -1 into consideration, why?
This is just the first half of the solution; but k is not used after this, as I determined by finding the text online; I’ll show the rest at the end, for those who want to see that there is nothing up our sleeves.
Do you see the problem? Hint: It’s in \(\displaystyle\frac{\epsilon}{|1-k|}\).
I answered:
I think you’re right to wonder about that; you’ve clearly learned to pay attention to details.
Why does he pay no attention to the division by 1 + k? I don’t know whether he completely missed that case, or perhaps just knows it doesn’t really matter. (I imagine him noticing a side road there and pondering whether to spend time exploring it, but just looking a little distance down it and realizing it doesn’t go anywhere.)
So you get to take his place. What would happen if k = -1? Will everything still work out, or not? Let me know what you find.
He probably should have written one sentence after saying y = kx to explain this. But he may have decided it was a good side road to send a wise student running on, while he gets some rest. He deserves it.
Have fun doing this! Please do answer my questions in red, so I can be sure you figured them out, and maybe we can talk more about them.
(In real time, both questions had been asked together, and I asked two red questions in one message.)
Kalyan replied:
What would happen if k = -1? Will everything still work out, or not?
When k = -1 then the limit becomes undefined. Maybe this is the reason that he did not take that.
Regards
I responded:
You said,
When k = -1 then the limit becomes undefined. Maybe this is the reason that he did not take that.
No, if the limit were undefined in that case, when the goal is to show that it is zero, then the proof would be utterly dead. It would be a felony to ignore that case!
The division by 1 + k comes much later than the place you need to focus on.
We want to find \(\displaystyle\underset{P\;\text{in}\;S_2}{\lim_{(x,y)\to(0,0)}}f(x,y)=\lim_{x\to0}(x+kx)\sin\frac{1}{x}\)
What does that mean if k = -1?
The division looked like something would go terribly wrong if \(k=-1\), so we need to think specifically about this case, and can’t ignore it.
The key to reading a proof is to take it step by step. Here, k was introduced in the line before this. So when you observe at the end of the proof that k = -1 would be a problem, you have to go back to where k was first mentioned, and consider what happens in that case.
What I would expect Leithold to have said here is something like, “Now, if k = -1, observe that … . In what follows, we will assume that k ≠ -1.” That will fix the problem, once you fill in the “…”. As I said, this will be a very short side path! That’s why I almost forgive him for not mentioning this.
Please answer the questions in red, again. I just want you to focus on the details I’ve asked about for now.
An author has to decide how much detail to show; if the student is expected to be growing in proof-reading skills, then what I call side paths just give the student more practice reading carefully, which is my goal here.
In the course of discussion, I restated the central question, and now he answered that:
2) What does the limit I quoted come to if k = -1? Just replace k with -1 in that limit expression!
We do not have to rack our brains to write the proof at all when k = -1 because, it is anyway 0, no matter what delta you get for a chosen epsilon.
If we set \(k=-1\), we get $$\displaystyle\underset{P\;\text{in}\;S_2}{\lim_{(x,y)\to(0,0)}}f(x,y)=\lim_{x\to0}(x+kx)\sin\frac{1}{x}=\lim_{x\to0}(x+(-1)x)\sin\frac{1}{x}=\lim_{x\to0}0\sin\frac{1}{x}=0$$
because it becomes a constant function whose value, and therefore limit, is 0. We can bypass the rest of the work for this case.
To put it another way, if \(k=-1\), then $$|x+kx|=|x-x|=0<\epsilon$$ for any x; so delta could be anything!
I replied,
Yes, you’ve seen it now.
In other words, we don’t need to think about epsilon and delta at all, because the limit of 0 is 0!
Further questions
Kalyan has long been interested in epsilon-delta proofs, and now re-opened some general concerns. I’ll split up his questions.
Doctor,
I would like to ‘go back’ once more with a list of FAQs regarding the epsilon-delta. I wonder you would not mind. I am going into everything step-by-step. Just an FAQ.
Q1. Why we call Epsilon- Delta a proof method? It has an exploration step where hardly the givens are used, we in fact use the results to come to know what is to be done in the actual work.
We’ve discussed an exploratory phase as preparation for proofs last time, as well as in discussing identities, and particularly in A Polynomial Inequality: Exploration vs Proof.
I replied:
I don’t call it a proof method! It’s a definition. A proof is a demonstration that such a definition is satisfied.
Any kind of proof will start with some sort of exploration, in which you think about how you can carry out the proof, followed by actually writing the proof. You plan, and then you do. What is unique in that? All of life works that way!
And of course you do consider the givens while you are exploring! But you aren’t yet proving anything, so you don’t start with the givens.
Kalyan again:
Q2.Wherever I see these problems of proof in Limits, in any book, I see that we have an ε, for which an apt δ is to be found that makes the curve go closer to the ‘target value’ for a δ that the user uses a margin so that his choice of ‘x’ (which controls a function of the form y = f(x)) is a significant choice.
This does not show any proof, it just like a ‘hunt-grab’ kind of thing. Does it mean that if I show that works for any epsilon and for some delta value, in a generalised form, it can called a proof?
For example in the sum of limits of functions proof:
Given: lim(x->a) f(x) = L and lim(x->a) g(x) = M.
By definition both the givens are expressed:
For a epsilon1>0, there is a delta1>0:
|f(x) – L| < epsilon1 when |x-a|< delta1
Similarly, for lim(x->a) g(x) = M:
For a epsilon2 >0, there is a delta2 > 0 :
|g(x)-M|<epsilon2 when |x-a|< delta2
Then, we see that it is a summation of limit problem, so we decide two epsilons to be such that when added gives epsilon.
epsilon1 = epsilon/2
epsilon2 = epsilon/2
Then, |f(x)-L| + |g(x)-M|< epsilon when |x-a|<delta where delta=min(delta_1,delta_2).
To summarise: Then, |f(x)-L| + |g(x)-M|< epsilon when |x-a|<delta where delta=min(delta_1,delta_2) means:
lim(x->a) (f(x) + g(x)) = L + M.
Is this what we call a proof? Just generalising things.
I answered:
If, at the end, you have shown that for any ε, you can find a suitable δ, then you have met the requirements of the definition, so you have a proof of the limit.
And all sorts of proof can look like “hunt and grab”. In many geometrical proofs, we draw an extra line and label some extra angles, and suddenly there is a proof. The reader may wonder, how did they know to draw that line? The answer is that the author took some time thinking about (a) what might be done, and (b) what will be useful, and tried them. When he found one that worked, he used that. That, again, is exploration, and when it is not explained, it can look like magic. But when what you want is a proof, you don’t need to explain how you thought of it. What matters is that the logic works.
Books I like explain how to find the proof; writing for mathematicians, that is not necessary. Authors do sometimes forget their audience – or that intended audience may not be you.
The proof of the limit of a sum has to show that the definition is satisfied. I don’t see that here.
That’s why, in planning a proof, we commonly write down the goal: What will we need to say just before we say QED? It’s this:
For any ε, there is a δ such that, whenever |x-a| < δ, it will be true that |[f(x)+g(x)] – lL+M]| < ε.
I don’t see that here. So, no, that is not a proof.
After this, I referred to an answer that I only realized later is included in A Closer Look at a Limit Proof, as an illustration that there are different ways to carry out such a proof; that idea was the subject of the last post, and this discussion with Kalyan was the inspiration for that.
The rest of the solution
In case you, like me, don’t like discussing a proof without seeing all of it, here is the end of the proof of question 2: