Recent questions have dealt with calculations of various parts of a segment of a circle (chord, arc, sagitta, etc.). How, for example, can you find the arc length if you know the chord length and the height? The definitive explanation of these questions is found in a classic page from Ask Dr. Math, written by Robert L. Ward (Doctor Rob). Here I am going to reproduce it in an updated format to make it more accessible.
Arc, Chord, Radius, Height, Angle, Apothem, and Area
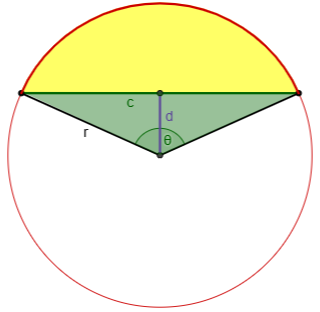
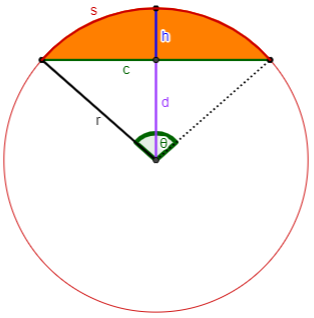
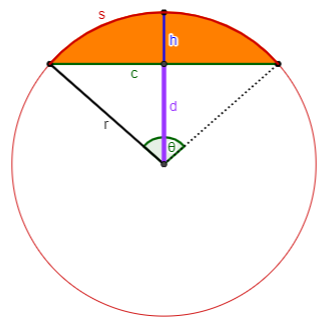
Suppose you have a segment of a circle, bounded by an arc of the circle and the chord subtending it:
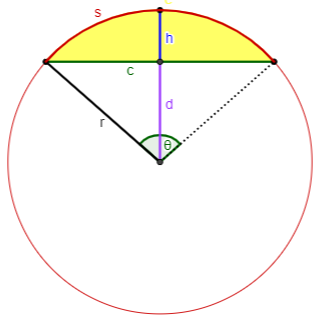
Let
- the length of the arc be s,
- the length of the chord be c,
- the radius of the circle be r,
- the distance from the midpoint of the chord to the midpoint of the arc be h (the height),
[This is also called the “sagitta”, or “arrow”, because of its resemblance to an arrow fitted to the string (chord) of a bow (arc) in archery; the constellation Sagittarius, the archer, comes from the same Greek.] - the measure in radians of the central angle subtending the arc be θ (where 0 ≤ θ ≤ π),
(Recall that 1 degree = π/180 radians.) - the distance from the midpoint of the chord to the center of the circle (the apothem) be d,
[This term comes from Greek for “place aside” or “put away” [from the center?]; it is properly used only when the chord is a side of a regular polygon, but I know of no other word for this!] - and the area be K.
For another diagram and formulas, see the Ask Dr. Math FAQ on the segment of a circle.
No one of these seven values is enough to determine the other six. Any two of them, however, are sufficient to determine the remaining five.
If you are given two of these values, how do you calculate the others? There are 21 cases. Click on the data you know from the table below.
Reader Dan Erb has programmed these cases into an Excel Spreadsheet, which is available for download. [I have modified it to make it a little easier to use; the original is here.]
Basic formulas
The formulas are based on several facts visible in the diagram.
From the sector with angle \(\theta\) and arc s, we see that $$s=r\theta$$
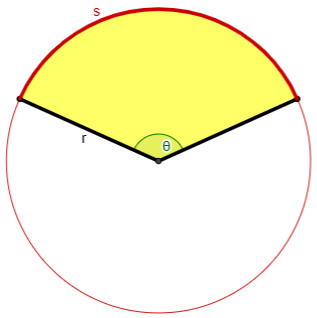
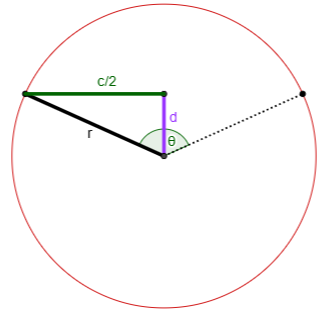
From the right triangle formed by the radius, apothem, and half-chord, we see that $$r^2=d^2+\left(\frac{c}{2}\right)^2\\\frac{d}{r}=\cos\left(\frac{\theta}{2}\right)\\\frac{c}{2r}=\sin\left(\frac{\theta}{2}\right)\\\frac{c}{2d}=\tan\left(\frac{\theta}{2}\right)$$
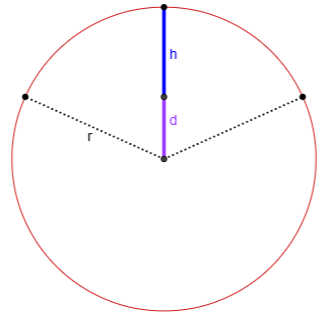
And we also see that $$r=h+d$$
Finally, the area of the segment is the area of the sector, minus the area of a triangle: $$K=\frac{1}{2}r^2\theta-\frac{1}{2}cd\\=\frac{1}{2}r^2\theta-\frac{1}{2}\left(2r\sin\left(\frac{\theta}{2}\right)\right)\left(r\cos\left(\frac{\theta}{2}\right)\right)\\=\frac{1}{2}r^2\theta-\frac{1}{2}r^2\sin\left(\theta\right)\\=r^2\frac{\theta-\sin(\theta)}{2}$$
Now we look at how to apply these basic formulas to each case.
The 21 cases
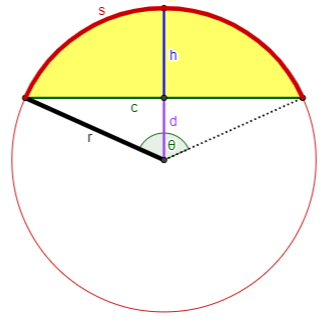
Case 1: You know s and c.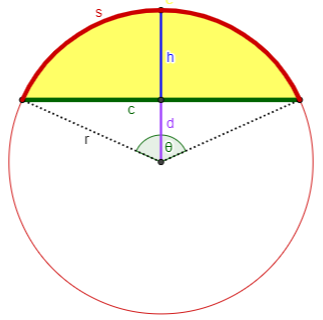
First solve $$\frac{c}{s}=\frac{\sin(x)}{x}$$ for x, which must be done numerically (see N1 below). Then $$\begin{aligned}\theta&=2x\\r&=\frac{s}{\theta}\\d&=r\cos(x)\\h&=r-d\\K&=r^2\frac{\theta-\sin(\theta)}{2}\end{aligned}$$
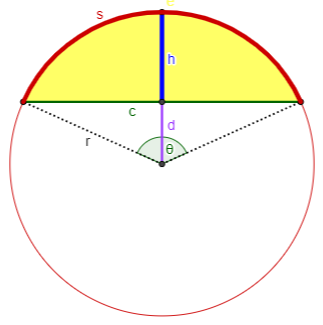
Case 2: You know s and r.
Calculate $$\begin{aligned}\theta&=\frac{s}{r}\\c&=2r\sin\left(\frac{\theta}{2}\right)\\d&=r\cos\left(\frac{\theta}{2}\right)\\h&=r-d\\K&=r^2\frac{\theta-\sin(\theta)}{2}\end{aligned}$$
Case 3: You know s and h.
First solve $$\frac{2h}{s}=\frac{1-\cos(x)}{x}$$ for x, which must be done numerically (see N3 below). Then $$\begin{aligned}\theta&=2x\\r&=\frac{s}{\theta}\\c&=2r\sin\left(x\right)\\d&=r-h\\K&=r^2\frac{\theta-\sin(\theta)}{2}\end{aligned}$$
Case 4: You know s and θ.
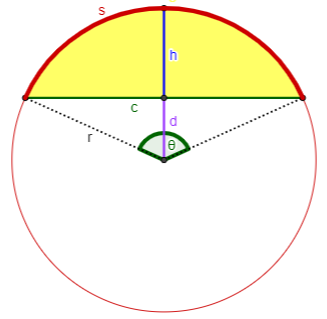
Calculate $$\begin{aligned}r&=\frac{s}{\theta}\\c&=2r\sin\left(\frac{\theta}{2}\right)\\d&=r\cos\left(\frac{\theta}{2}\right)\\h&=r-d\\K&=r^2\frac{\theta-\sin(\theta)}{2}\end{aligned}$$
Case 5: You know s and d.
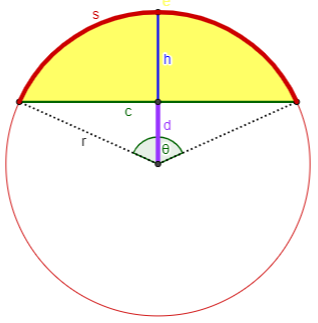
First solve $$\frac{2d}{s}=\frac{\cos(x)}{x}$$ for x, which must be done numerically (see N5 below). Then $$\begin{aligned}\theta&=2x\\r&=\frac{s}{\theta}\\c&=2r\sin\left(x\right)\\h&=r-d\\K&=r^2\frac{\theta-\sin(\theta)}{2}\end{aligned}$$
Case 6: You know s and K.
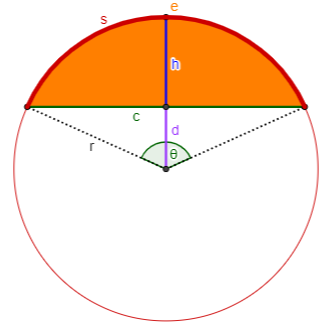
First solve $$\frac{2K}{s^2}=\frac{\theta-\sin(\theta)}{\theta^2}$$ for θ, which must be done numerically (see N6 below). Then $$\begin{aligned}r&=\frac{s}{\theta}\\c&=2r\sin\left(\frac{\theta}{2}\right)\\d&=r\cos\left(\frac{\theta}{2}\right)\\h&=r-d\end{aligned}$$
Case 7: You know c and r.
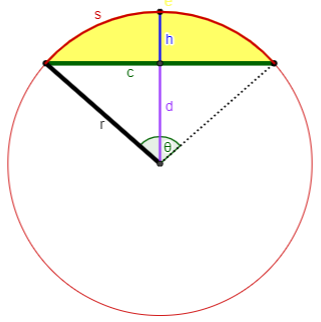
Calculate $$\begin{aligned}\theta&=2\arcsin\left(\frac{c}{2r}\right)\\s&=r\theta\\d&=r\cos\left(\frac{\theta}{2}\right)\\h&=r-d\\K&=r^2\frac{\theta-\sin(\theta)}{2}\end{aligned}$$
Case 8: You know c and h.
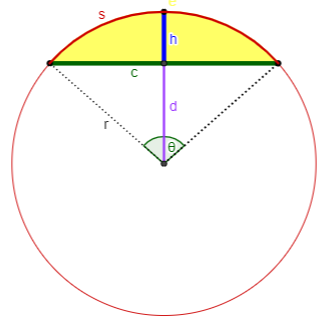
Calculate $$\begin{aligned}r&=\frac{c^2+4h^2}{8h}\\\theta&=2\arcsin\left(\frac{c}{2r}\right)\\s&=r\theta\\d&=r-h\\K&=r^2\frac{\theta-\sin(\theta)}{2}\end{aligned}$$
Case 9: You know c and θ.
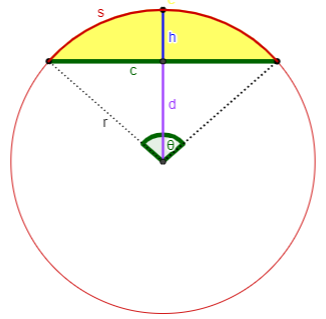
Calculate $$\begin{aligned}r&=\frac{c}{2\sin\left(\frac{\theta}{2}\right)}\\s&=r\theta\\d&=r\cos\left(\frac{\theta}{2}\right)\\h&=d-r\\K&=r^2\frac{\theta-\sin(\theta)}{2}\end{aligned}$$
Case 10: You know c and d.
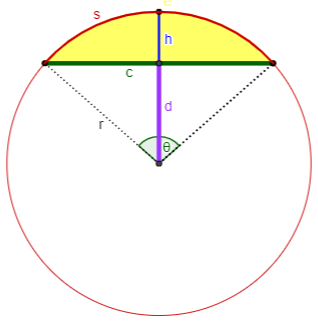
Calculate $$\begin{aligned}r&=\frac{\sqrt{c^2+4d^2}}{2}\\h&=r-d\\\theta&=2\arcsin\left(\frac{c}{2r}\right)\\s&=r\theta\\K&=r^2\frac{\theta-\sin(\theta)}{2}\end{aligned}$$
Case 11: You know c and K.
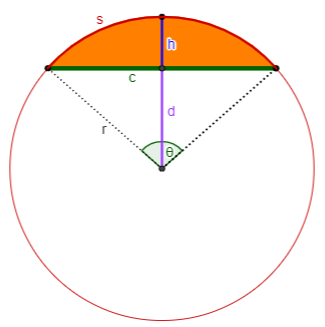
First solve $$\frac{4K}{c^2}=\frac{\theta-\sin(\theta)}{1-\cos(\theta)}$$ for θ, which must be done numerically (see N11 below). Then $$\begin{aligned}r&=\frac{c}{2\sin\left(\frac{\theta}{2}\right)}\\s&=r\theta\\d&=r\cos\left(\frac{\theta}{2}\right)\\h&=r-d\end{aligned}$$
Case 12: You know r and h.
Calculate $$\begin{aligned}d&=r-h\\\theta&=2\arccos\left(\frac{d}{r}\right)\\c&=2r\sin\left(\frac{\theta}{2}\right)\\s&=r\theta\\K&=r^2\frac{\theta-\sin(\theta)}{2}\end{aligned}$$
Case 13: You know r and θ.
Calculate $$\begin{aligned}s&=r\theta\\d&=r\cos\left(\frac{\theta}{2}\right)\\h&=r-d\\c&=2r\sin\left(\frac{\theta}{2}\right)\\K&=r^2\frac{\theta-\sin(\theta)}{2}\end{aligned}$$
Case 14: You know r and d.
Calculate $$\begin{aligned}h&=r-d\\\theta&=2\arccos\left(\frac{d}{r}\right)\\c&=2r\sin\left(\frac{\theta}{2}\right)\\s&=r\theta\\K&=r^2\frac{\theta-\sin(\theta)}{2}\end{aligned}$$
Case 15: You know r and K.
First solve $$\frac{2K}{r^2}=\theta-\sin(\theta)$$ for θ, which must be done numerically (see N15 below). Then $$\begin{aligned}s&=r\theta\\c&=2r\sin\left(\frac{\theta}{2}\right)\\d&=r\cos\left(\frac{\theta}{2}\right)\\h&=r-d\end{aligned}$$
Case 16: You know h and θ.
Calculate $$\begin{aligned}r&=\frac{h}{1-\cos\left(\frac{\theta}{2}\right)}\\d&=r-h\\c&=2r\sin\left(\frac{\theta}{2}\right)\\s&=r\theta\\K&=r^2\frac{\theta-\sin(\theta)}{2}\end{aligned}$$
Case 17: You know h and d.
Calculate $$\begin{aligned}r&=h+d\\\theta&=2\arccos\left(\frac{d}{r}\right)\\c&=2r\sin\left(\frac{\theta}{2}\right)\\s&=r\theta\\K&=r^2\frac{\theta-\sin(\theta)}{2}\end{aligned}$$
Case 18: You know h and K.
First solve $$\frac{2K}{h^2}=\frac{\theta-\sin(\theta)}{\left(1-\cos\left(\frac{\theta}{2}\right)\right)^2}$$ for θ, which must be done numerically (see N18 below). Then $$\begin{aligned}r&=\sqrt{\frac{2K}{\theta-\sin\left(\theta\right)}}\\d&=r-h\\c&=2r\sin\left(\frac{\theta}{2}\right)\\s&=r\theta\end{aligned}$$
Case 19: You know θ and d.
Calculate $$\begin{aligned}r&=\frac{d}{\cos\left(\frac{\theta}{2}\right)}\\h&=r-d\\c&=2d\tan\left(\frac{\theta}{2}\right)\\s&=r\theta\\K&=r^2\frac{\theta-\sin(\theta)}{2}\end{aligned}$$
Case 20: You know θ and K.
Calculate $$\begin{aligned}r&=\sqrt{\frac{2K}{\theta-\sin\left(\theta\right)}}\\s&=r\theta\\d&=r\cos\left(\frac{\theta}{2}\right)\\h&=r-d\\c&=2r\sin\left(\frac{\theta}{2}\right)\end{aligned}$$
Case 21: You know d and K.
First solve $$\frac{K}{d^2}=\frac{\theta-\sin(\theta)}{1+\cos\left(\theta\right)}$$ for θ, which must be done numerically (see N21 below). Then $$\begin{aligned}r&=\frac{d}{\cos\left(\frac{\theta}{2}\right)}\\h&=r-d\\c&=2r\sin\left(\frac{\theta}{2}\right)\\s&=r\theta\end{aligned}$$
Numerical Solutions: Newton’s Method
The equation \(f(x)=0\) can be solved numerically using (Sir Isaac) Newton’s Method as follows.
Guess a starting value \(x_0\). This will depend heavily on the form of \(f(x)\). Then for each \(n=0,1,2,\dots\), compute
\(x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}\),
where \(f'(x)\) is the derivative of \(f(x)\) with respect to \(x\). Continue this until \(|x_{n+1}-x_n|\) is smaller than the accuracy sought. Then \(x_{n+1}\) agrees with the actual root to at least that level of accuracy.
If the starting value for \(x_0\) is close enough to a root, this will converge, and very rapidly. If \(x_0\) is rather far from a root, this process may diverge, or exhibit other undesirable behavior.
N1 (Given s and c):
To solve, for example, \(\displaystyle \frac{\sin(x)}{x}=k\) for some constant \(k>0\) (Case 1 above), is the same as finding a root of the equation
\(\displaystyle f(x)=\sin(x)-kx=0\).
This can be done using Newton’s Method as follows.
Guess a starting value of
\(\displaystyle x_0=\sqrt{6-6k}\).
Then for each \(n=0,1,2,\dots\), compute
\(\displaystyle x_{n+1}=x_n-\frac{\sin(x_n)-kx_n}{\cos(x_n)-k}\).
Example: Solve sin(x)/x = 3/4 to five decimal places of accuracy. We carry seven places of accuracy in our calculations:
n x(n) sin(x[n]) cos(x[n]) sin(x[n])/x(n)
========================================================
0 1.2247449 0.9407193 0.3391860 0.7680941
1 1.2786882 0.9576389 0.2879717 0.7489229
2 1.2757074 0.9567763 0.2908250 0.7499967
3 1.2756981 0.9567736 0.2908338 0.7500000
4 1.2756981
Since |x(4)-x(3)| < 0.000005, we have the answer correct to five decimal places, x = 1.27570.
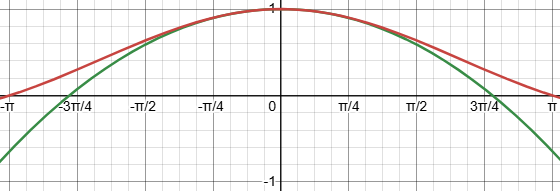
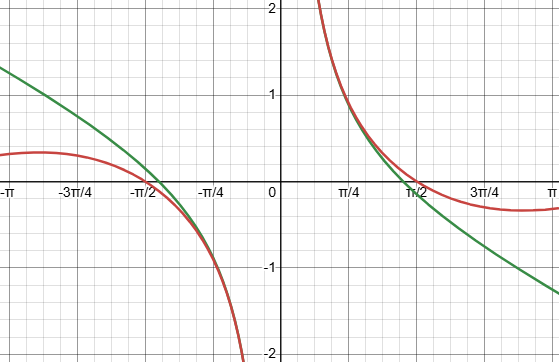
Explanation: Why does he start with \(\displaystyle x_0=\sqrt{6-6k}\)? By approximating \(\displaystyle\frac{\sin(x)}{x}\) with the first two terms of the Taylor series for \(\sin(x)\), namely \(\displaystyle\frac{x-\frac{x^3}{6}}{x}\), we want to solve \(1-\frac{x^2}{6}=k\) for x; we get \(\displaystyle x=\sqrt{6-6k}\). This is a good first approximation (in green below) to the actual function (in red) when \(|x|<\frac{\pi}{2}\) (as it will always be here):
Alternative method: series
There is also an infinite series which can solve \(\frac{\sin(x)}{x}=k\), \(0<x\le\pi\). Let \(y=1-k\). Then \(0<y<1\), and the following infinite series converges in this range:
x = sqrt(6y)(1 +
3y/20 +
321y2/5600 +
3197y3/112000 +
445617y4/27596800 +
1766784699y5/179379200000 + ...).
This converges rapidly for large values of \(k=1-y\).
Another series is
x = π/(1+k) -
(π3k3/6)(1 -
4k +
[10+9π2/20]k2 -
[20+16 π2/5]k3 +
...),
= π/(1+k) -
(π3k3/[6(1+k)4]) -
(3π5k5/40)(1 - 64k/9 + ...).
This converges rapidly for small values of k.
N3 (Given s, h):
Newton’s Method works for \(\displaystyle \frac{1-\cos(x)}{x}=k\) (Case 3 above), with the initial start
\(\displaystyle x_0=2k\)
and iteration
\(\displaystyle x_{n+1}=x_n-\frac{\cos(x_n)+kx_n-1}{-\sin(x_n)+k}\).
Explanation: Here, we are approximating \(\displaystyle\frac{1-\cos(x)}{x}\) using the first two terms of the series for \(\cos(x)\), namely \(\displaystyle\frac{1-\left(1-\frac{x^2}{2}\right)}{x}=\frac{x}{2}=k\), and solving this for x yields \(\displaystyle x=2k\).
Then we use Newton’s method to find a root of \(1-\cos(x)-kx=0\).
N5 (Given s, d):
Newton’s Method works for \(\displaystyle \frac{\cos(x)}{x}=k\) (Case 5 above) with the initial start
\(\displaystyle x_0=\sqrt{2+k^2}-k\)
and iteration
\(\displaystyle x_{n+1}=x_n-\frac{\cos(x_n)-kx_n}{-\sin(x_n)-k}\).
Explanation: Here, we are approximating \(\displaystyle \frac{\cos(x)}{x}\) using the first two terms of the series for \(\cos(x)\), namely \(\displaystyle\frac{1-\frac{x^2}{2}}{x}=\frac{2-x^2}{2x}=k\), and solving this for (positive) x yields \(\displaystyle x=\sqrt{2+k^2}-k\).
Then we use Newton’s method to find a root of \(\cos(x)-kx=0\).
N6 (Given s, K):
Newton’s Method works for \(\displaystyle\frac{t-\sin(t)}{t^2}=k\) (Case 6 above), with the initial start
\(\displaystyle t_0=6k\)
and iteration
\(\displaystyle t_{n+1}=t_n-\frac{kt_n^2-t_n+\sin(t_n)}{2kt_n-1+\cos(t_n)}\).
Explanation: Here, we are approximating \(\displaystyle\frac{t-\sin(t)}{t^2}\) using the first two terms of the series for \(\sin(x)\), namely \(\displaystyle\frac{t-\sin(t)}{t^2}=\frac{t-\left(t-\frac{t^3}{6}\right)}{t^2}=\frac{t}{6}=k\), and solving this for t yields \(\displaystyle t=6k\).
Then we use Newton’s method to find a root of \(t-\sin(x)-kt^2=0\).
N11 (Given c, K):
Newton’s Method works for \(\displaystyle\frac{t-\sin(t)}{1-\cos(t)}=k\) (Case 11 above), with the initial start
\(\displaystyle t_0=3k\)
and iteration
\(\displaystyle t_{n+1}=t_n-\frac{k\cos(t_n)-\sin(t_n)+t_n-k}{1-k\sin(t_n)-\cos(t_n)}\).
Explanation: Here, we can approximating the numerator and denominator of \(\displaystyle\frac{t-\sin(t)}{1-\cos(t)}=k\) using the first two terms of the series for \(\sin(x)\) and \(\cos(x)\) respectively, namely \(\displaystyle\frac{t-\left(t-\frac{t^3}{6}\right)}{1-\left(1-\frac{t^2}{2}\right)}=\frac{\frac{t^3}{6}}{\frac{t^2}{2}}=\frac{t}{3}=k\), and solving this for t yields \(\displaystyle t=3k\).
Then we use Newton’s method to find a root of \(t-\sin(x)-k(1-\cos(t))=0\).
N15 (Given r, K):
Newton’s Method works for \(\displaystyle t-\sin(t)=k\) (Case 15 above), with the initial start
\(\displaystyle t_0=(6k)^{1/3}\)
and iteration
\(\displaystyle t_{n+1}=t_n-\frac{t_n-\sin(t_n)-k}{1-\cos(t_n)}\).
Explanation: Here, we are approximating \(\displaystyle t-\sin(t)\) using the first two terms of the series for \(\sin(x)\), namely \(\displaystyle t-\sin(t)=t-\left(t-\frac{t^3}{6}\right)=\frac{t^3}{6}=k\), and solving this for t yields \(\displaystyle t=\sqrt[3]{6k}\).
Then we use Newton’s method to find a root of \(t-\sin(x)-k=0\).
N18 (Given h, K):
Newton’s Method works for \(\displaystyle \frac{t-\sin(t)}{\left(1-\cos\left(\frac{t}{2}\right)\right)^2}=k\) (Case 18 above), with the initial start
\(\displaystyle t_0=\frac{32}{3k}\)
and iteration
\(\displaystyle t_{n+1}=t_n-\frac{k\left(1-\cos\left(\frac{t}{2}\right)\right)^2-t_n+\sin(t_n)}{k\sin\left(\frac{t_n}{2}\right)-\frac{k\sin(t_n)}{2}-1+\cos(t_n)}\).
Explanation: Here, we can approximating the numerator and denominator of \(\displaystyle \frac{t-\sin(t)}{\left(1-\cos\left(\frac{t}{2}\right)\right)^2}\) using the first two terms of the series for \(\sin(x)\) and \(\cos\left(\frac{t}{2}\right)\) respectively, namely $$\displaystyle\frac{t-\left(t-\frac{t^3}{6}\right)}{\left(1-\left(1-\frac{\left(\frac{t}{2}\right)^2}{2}\right)\right)^2}=\frac{\frac{t^3}{6}}{\left(\frac{t^2}{8}\right)^2}=\frac{\frac{t^3}{6}}{\frac{t^4}{64}}=\frac{32}{3t}=k$$ and solving this for t yields \(\displaystyle t=\frac{32}{3k}\).
Then we use Newton’s method to find a root of \(t-\sin(x)-k\left(1-\cos\left(\frac{t}{2}\right)\right)^2=0\).
N21 (Given d, K):
Newton’s Method works for \(\displaystyle \frac{t-\sin(t)}{1+\cos\left(t\right)}=k\) (Case 21 above), with the initial start
\(\displaystyle t_0=(12k)^{1/3}\)
and iteration
\(\displaystyle t_{n+1}=t_n-\frac{t_n-\sin(t_n)-k\cos(t_n)-k}{1-\cos(t_n)+k\sin(t_n)}\).
Explanation: Here, we can approximating the numerator and denominator of \(\displaystyle\frac{t-\sin(t)}{1+\cos(t)}=k\) using the first two terms of the series for \(\sin(x)\) and \(\cos(x)\) respectively, namely \(\displaystyle\frac{t-\left(t-\frac{t^3}{6}\right)}{1+\left(1-\frac{t^2}{2}\right)}=\frac{\frac{t^3}{6}}{2-\frac{t^2}{2}}\approx\frac{\frac{t^3}{6}}{2}=\frac{t^3}{12}=k\), and solving this for t yields \(\displaystyle t=(12k)^{1/3}\). (Here we ignored the second term of the cosine series because that is negligible compared to the first.)
Then we use Newton’s method to find a root of \(t-\sin(x)-k\left(1+\cos(t)\right)^2=0\).
NOTE: In experimenting with the spreadsheet, I found that this case doesn’t always work – not primarily because the initial approximation is poor, but because Newton’s method does not converge to the right solution for all values of k. More study will be needed to correct this.
One Additional Situation
If you know the fraction of the area \(\displaystyle F=\frac{K}{r^2}\), and you want to compute the fraction of the height \(\displaystyle \frac{h}{2r}\), this can also be done. That means you know \(2F=\theta-\sin(\theta)\), and you want to find θ. You must do this numerically. You can use Newton’s Method for this, as well:
\(\displaystyle t_0=(12F)^{1/3}\)
\(\displaystyle t_{n+1}=\frac{\sin(t_n)-t_n\cos(t_n)+2F}{1-\cos(t_n)}\)
for \(n=0,1,2,3,\dots\). The sequence \(t_n\) will converge to θ. Then
\(\displaystyle \frac{h}{2r}=\frac{1-\cos\left(\frac{\theta}{2}\right)}{2}\).
Addenda
Case 8 is touched upon in Distances to an Arc: Exact and Approximate Formulas.
Case 13 is discussed in A Tunnel Through the Earth.
Case 12 and case 15 are implicitly used in Measuring Water in a Tank, for the direct (finding the volume from a dipstick) and inverse (finding the level at which a tank is, say, 1/4 full) problems, respectively.

Pingback: Solving Equations with Newton’s Method – The Math Doctors