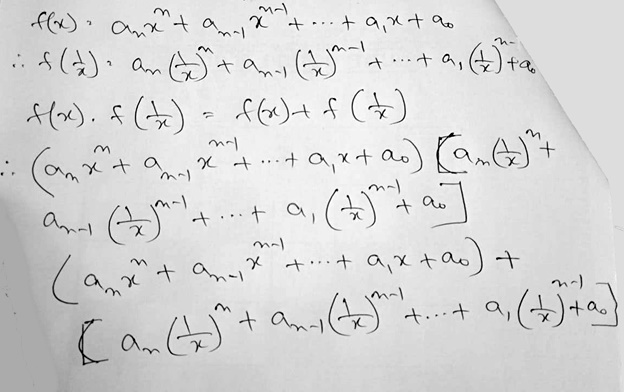Looking back at interesting questions I had to skip over when there were too many to choose, I found this interesting discussion of a functional equation.
A beautiful problem
It comes from Debarghya, in June 2023, under the title “Polynomial function”:
While solving a problem I have seen an equation
f(x).f(1/x) = f(x) + f(1/x).
On searching over internet, I have seen that this statement is true only when f(x) = 1 ± xn. How can this be true? Moreover this equation looks beautiful. Does it have any special significance? Please help.
The equation is $$f(x)\cdot f\left(\frac{1}{x}\right)=f(x)+f\left(\frac{1}{x}\right)$$ That is, the product of the two functions equals their sum (for every value of x).
This sort of problem, relating values of a function for different inputs, is not typically taught in elementary algebra, but can be very interesting, and doesn’t require a lot of knowledge for simple problems.
Restating the problem
Doctor Rick answered:
Hi, Debarghya.
I would like to see where you saw this, for more background. Where did you find the solution to this equation? Did it give a proof? What was the mathematical context?
I’ll show you where I see beauty here. Let’s solve the equation for f(1/x):
f(x) f(1/x) = f(x) + f(1/x) [1]
f(x) f(1/x) – f(1/x) = f(x)
f(1/x)(f(x) – 1) = f(x)
f(1/x) = f(x)/(f(x) – 1)
f(1/x) = (f(x) – 1 + 1)/(f(x) – 1)
f(1/x) = 1 + 1/(f(x) – 1)
He has just rearranged the equation to get \(f\left(\frac{1}{x}\right)\) alone on one side, whereas the original form is symmetrical, treating that and \(f(x)\) interchangeably. The last step amounts to a long division, which allows \(f(x)\) to appear in only one place. Taking it one step further, we can see this as $$f\left(\frac{1}{x}\right)-1=\frac{1}{f(x)-1},$$ which shows a different sort of symmetry.
This form gives me the idea of defining a new function:
g(x) = f(x) – 1
In terms of g, we have
g(1/x) = 1/g(x) [2]
This is very interesting! It says that g applied to the reciprocal of x is equal to the reciprocal of g(x). We can rephrase our problem (though the language may not be familiar to you):
What functions commute with the reciprocal function under composition?
That is, we’re looking for all functions g for which we can switch the order in which the two functions, g and 1/x, are applied, and the result doesn’t change. When we subtract 1 from each such function, we’ll get a function that meets the conditions of the original problem.
The new function satisfies $$g\left(\frac{1}{x}\right)=\frac{1}{g(x)},$$ or, equivalently, $$g(x)g\left(\frac{1}{x}\right)=1.$$
So solving the new, simpler, problem will solve the original.
Confirming a solution vs proving uniqueness
Continuing …
It’s easy to confirm that f(x) = 1 ± xn is a solution to [1], or equivalently that g(x) = ±xn is a solution to [2]. The hard part is to prove that these are the only solutions. I suspect that a full proof would be beyond your ability, and likely beyond mine. However, since your subject line was “polynomial function”, perhaps it will be sufficient for your purposes to show that the family g(x) = ±xn are the only polynomial functions with this property.
We’ll soon see the confirmation (check) of the claimed answer, and we’ll eventually prove its uniqueness among polynomials.
You might give this a try! It doesn’t require any special knowledge, though it may be unlike the things you have done so far with polynomials. I’d start by writing a general polynomial like this:
p(x) = anxn + an-1xn-1 + … + a1x + a0
where an ≠ 0 (so that p(x) is a polynomial of degree n). Would you like to try this?
Keep in mind that this is just a way to start thinking about the problem, not necessarily an efficient way to solve it.
It does have to be a polynomial
A few minutes later, I jumped in:
Hi, Debarghya.
Rather than try to solve this on my own, I searched for similar problems online (to see what you might have seen) and found several. Some of them specify that f(x) has to be a polynomial, and prove that, as Doctor Rick suggests, f(x) = 1 ± xn is the only polynomial solution. So, hopefully, that is what your source said. Some sites mention in passing that if you don’t require a polynomial, there are in fact many solutions (especially if you consider a piecewise solution, which is perfectly valid as a function).
But other sites ask questions like, “If f(x) is a function satisfying f(x)* f(1/x) = f(x) + f(1/x) and f(4) = 65, what will be the value of f(6)?” Without the restriction to polynomials, this has no answer! So such a site is just wrong.
So I recommend doing just what Doctor Rick suggests: Pursue the problem given that f is a polynomial. I imagine there are several ways to fill in the details.
Starting to think about it
Debarghya replied, trying the suggestion:
Sorry Dr. I could not solve how 1 ± xn could be the solution of given function. After two steps it messed up. I am showing my work. Please help.
And the website where I saw this issue is
He is trying to work with a general polynomial directly, which would be very difficult, but at least clarifies what we want to prove.
The source asks the question,
If f(x) be a polynomial function satisfying f(x)f(1/x) = f(x) + f(1/x) and f(4) = 65. Then, find f(6).
It then gives a solution, starting much like Doctor Rick’s idea.
I responded:
It’s good to see that your source stated the problem correctly, requiring the function to be a polynomial. This was one of the places I had found.
When you say,
I could not solve how 1 ± xn could be the solution of given function
there are two different issues: how to obtain that solution (solve), and how to check that it is really valid for all n.
Solving means finding a solution, and hopefully all solutions; that is presumably Debarghya’s goal.
Incidentally, in case you haven’t noticed it, this is a “functional equation” whose general solution is a class of equations (where n and the sign can vary); the additional condition allows you to choose one particular solution that satisfies both the functional equation and the condition.
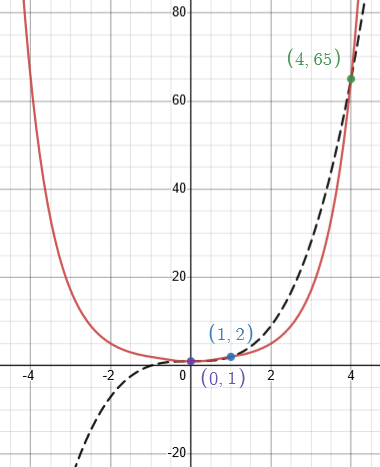
The general solution, as we’ve been told, is \(f(x)=1\pm x^n\), which means that any such function satisfies the equation; and given that \(f(4)=65\), we can determine that, since \(f(4)=1\pm 4^n=65\), we must have \(\pm4^n=64\), so \(n=3\) and the sign is positive, making the particular solution \(f(x)=1+x^3\). The entire family of solutions is suggested by this graph (where I’ve taken \(n={\color{Blue}0},{\color{DarkGreen}1},{\color{Orange}2},{\color{Red}3}\), with solid lines for addition and broken for subtraction):
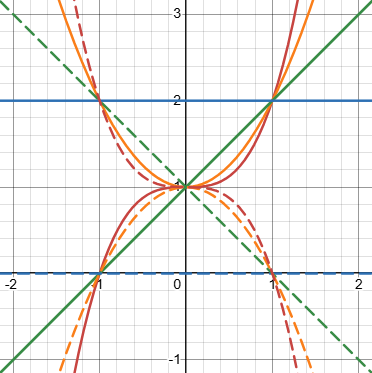
You may notice something interesting that these graphs all have in common; we can see this by taking specific values for the variable, which is a common technique in solving simple functional equations. We have the equation $$f(x)f\left(\frac{1}{x}\right)=f(x)+f\left(\frac{1}{x}\right);$$ if we take \(x=1\), this becomes \(f(1)f\left(1\right)=f(1)+f\left(1\right)\), which implies that \(f(1)^2=2f(1)\), so that \(f(1)=0\text{ or }2\). All the curves pass through either \((1,0)\) or \((1,2)\).
Also, if we take \(x=\infty\) (actually a limit), and use the g form of the equation, $$g\left(\frac{1}{x}\right)=\frac{1}{g(x)},$$ we find that \(g\left(\frac{1}{\infty}\right)=\frac{1}{g(\infty)}\), that is, \(g\left(0\right)=\frac{1}{g(\infty)}\). But if g is a (non-constant) polynomial function, it approaches \(\pm\infty\) at infinity, so this becomes \(g\left(0\right)=\frac{1}{\infty}=0\). Adding 1 to this, \(f(0)=1\), so all the curves (except for the \(n=0\) case) pass through \((0,1)\).
Checking the claimed solution
Checking the particular solution, x3 + 1, is not hard, and will be a good place to start. Just evaluate both sides of
(x3 + 1)((1/x)3 + 1) = (x3 + 1) + ((1/x)3 + 1)
You will see that this works; you may also find that this helps you see how the problem works. (I find it helpful to rewrite (1/x)3 as x-3.)
You may want to try checking other particular solutions, such as x5 + 1, or even the general solution xn + 1, in the same way.
Carrying out this check, the left-hand side becomes $$(x^3+1)(x^{-3}+1)=1+x^3+x^{-3}+1=x^3+2+x^{-3}$$ while the right-hand side becomes $$(x^3+1)+(x^{-3}+1)=x^3+2+x^{-3}$$ and they are clearly the same function.
For the general solution with an addition, we have, similarly, $$(x^n+1)(x^{-n}+1)=1+x^n+x^{-n}+1=x^n+2+x^{-n}\\(x^n+1)+(x^{-n}+1)=x^n+2+x^{-n}$$ which are equal.
And for the subtraction, we have $$(1-x^n)(1-x^{-n})=1-x^{-n}-x^n+1=2-x^n-x^{-n}\\(1-x^n)+(1-x^{-n})=1-x^n-x^{-n}$$ again showing that it works.
But your work appears to be an attempt to solve the problem by “brute force”, expanding the entire equation for a general polynomial, which would not be easy, and perhaps is practically impossible. You might, though, try doing your work for a specific case, such as supposing that f is a cubic polynomial (n = 3). This would at least give you a sense of what the general case would involve, and might even suggest a trick you could use for the general case.
Solving is commonly much harder than checking an answer; and it is really the latter, not the former, that confirms the solution. If you don’t believe an answer, then checking is what you need to do to convince yourself!
Unfortunately, you can’t check that the solution you have is the only one, only that it is one!
Have you tried to follow their thinking, which takes a very different path than yours? There is one step that to my mind is a big leap, and which they seem to assume has already been proved. (Perhaps it is a theorem in their curriculum?) But most of the work is what I would do: solving for f(1/x) in terms of f(x), or vice versa, and then observing a pattern that suggests a substitution. The leap, which they don’t explain, is in saying that f(x) – 1 must be ±xn. (I can see that it is true, but not how it would be “obvious” enough not to need any explanation!) I’d like to hear your thoughts on this.
The claim on the site (in our terms) is that if \(g(x)g\left(\frac{1}{x}\right)=1\), then \(g(x)=\pm x^n\) for some n. We’d like to prove this.
Several sites I found give the same solution almost word for word, suggesting that this is a classic problem that people just learn, rather than one that many people have solved independently! Don’t be surprised that you are having trouble with it. I would, too (though not quite as much).
Trying brute force for a small case
Doctor Rick had more to say:
I’d like to add to what Doctor Peterson said, from my perspective.
Looking at the link where you got the problem, I see that the author arrived at the same point I did, namely that
g(x) = f(x) – 1 and g(1/x) = f(1/x) – 1 are reciprocals of one another
though perhaps in a more roundabout way than what I showed you. The next step is what I wanted you to try: to prove that a polynomial g(x) such that g(1/x) = 1/g(x) must be of the form ±xn. To me, this is the interesting part of the problem — but the author, rather than solving it, just assumes that we know this already!
What you tried to do was to start at the beginning of the problem,
f(x) f(1/x) = f(x) + f(1/x).
I think it’s easier to start with my restatement in the form
g(x) g(1/x) = 1.
Doctor Peterson has given you some clues about this: try it first assuming the polynomial has a particular degree, maybe even 2 (a quadratic); write 1/x as x–1.
I’ve tried this for a cubic, and sticking with f instead of g, and didn’t enjoy the experience!
Let’s do it his way:
Suppose that \(g(x)=ax^2+bx+c\).
Then \(g\left(\frac{1}{x}\right)=ax^{-2}+bx^{-1}+c\). We want
$$g(x)g\left(\frac{1}{x}\right)=(ax^2+bx+c)(ax^{-2}+bx^{-1}+c)=1$$ Expanding the LHS, $$a^2+abx+acx^2+abx^{-1}+b^2+bcx+acx^{-2}+bcx^{-1}+c^2\\=acx^2+(ab+bc)x+(a^2+b^2+c^2)+(ab+bc)x^{-1}+acx^{-2}$$
We want this to equal 1 (for all x), so we set the coefficients equal: $$ac=0\\ab+bc=0\\a^2+b^2+c^2=1\\ab+bc=0\\ac=0$$
This tells us that either a or c is zero, and either b is zero or \(a+c=0\). Putting this together, we find that \((a,b,c)\) is one of \((0,0,1)\), \((0,0,-1)\), \((0,1,0)\), \((0,-1,0)\), \((1,0,0)\), and \((-1,0,0)\). These yield the polynomial functions $$g(x)=1\\g(x)=-1\\g(x)=x\\g(x)=-x\\g(x)=x^2\\g(x)=-x^2,$$ that is, \(g(x)=\pm x^n\). So $$f(x)=0\\f(x)=2\\f(x)=1+x\\f(x)=1-x\\f(x)=1+x^2\\f(x)=1-x^2,$$ as we expected.
So it works; but clearly this is not a good way to solve the full problem! It doesn’t give us any insight that could lead to a full proof.
But can we back up a bit, and see something that would simplify the work?
One thing we might observe is that $$g\left(\frac{1}{x}\right)=ax^{-2}+bx^{-1}+c=\frac{a+bx+cx^2}{x^2},$$ where the numerator is the same polynomial with the coefficients reversed. We might invent a notation for this reversed polynomial, say \(g_r(x)=cx^2+bx+a\). This generalizes to any degree. So the equation says that (if g is any polynomial of degree n) $$g(x)\cdot\frac{g_r(x)}{x^n}=1.$$ We’ll use this below.
In addition, you will need to understand one thing about “functional equations”. We want to establish that two polynomial functions are the same function — not merely that they have the same value for some particular value of x, but that their values are the same for every value of x. You may not have encountered this kind of problem before, so here’s a tip: It can be proved that two polynomials are the same function if, and only if, their coefficients are the same. For instance,
a2x2 + a1x + a0 ≡ b2x2 + b1x + b0
if and only if a2 = b2, a1 = b1, and a0 = b0.
The symbol \(\equiv\) means “is identically equal to”, that is, “is equal for any value of the variable(s)”.
Functional equations force you to think a little differently: Rather than solving for a value of x, you are solving for a function f that makes the equation true for all values of x!
Doing the check
Debarghya replied:
Now I got it.
g(x)g(1/x) = 1
for g(x) = xn we get
g(x)g(1/x) = xn (1/xn ) = 1
similarly for g(x) = – xn we get
g(x)g(1/x) = – xn (- 1/xn ) = 1
thus, g(x) = ±xn. so, g(x) = f(x) – 1 or, ±xn = f(x) – 1 or, f(x) = 1 ± xn
so, 1 ± xn is the solution of f(x) which satisfies the equation f(x) f(1/x) = f(x) + f(1/x)
I should have solved it earlier. It is very easy. although proving it to be true as only solution of the equation is beyond my reach. but now it is not much required for my course of study.
This is, again, just a check of the claimed answer; but using the modified formulation does make that easier.
Doctor Rick was still curious:
If you are satisfied for now, we’re OK. I had the impression from the start that this was not part of your curriculum but rather something you were exploring on your own. Confirming the given solution is, as you say, easy; but finding that solution is not so easy, and as you have seen, proving that there are no other solutions takes it to another level!
You said at the start, “while solving a problem I have seen an equation f(x).f(1/x) = f(x) + f(1/x).” Was the problem you were solving part of your curriculum? How was this equation related to the problem you were trying to solve? I ask merely out of my own curiosity, so you can feel free not to answer.
Debarghya replied:
Functional equation is not part of my curriculum. I have seen such equation first time. Actually I look after problems on functions over various books and worksheets/videos on internet. I also refer to advanced functions by Nelson. When problems I encounter are beyond my understanding then I look after solutions if they are provided. When there is no solution or I doubt the way they are solved then you are my only pathfinder.
As far as this problem is concerned, I intended to find the general solution of g(x)g(1/x) = 1 from mere curiosity. I am not satisfied by checking that 1 ± xn is the solution of g(x)g(1/x) = 1. Rather I want to know, is this the only solution or, what is the general solution of g(x)g(1/x) = 1? but I understood that this requires some more knowledge about polynomial functions and functional equations. So, I will learn more about them and then dive again into finding that. I am not giving up. I am taking a pause for a while.
There are two things left to do.
Proving these are the only polynomial solutions
We never did get to the actual proof in this discussion. Let’s do it, starting with my observation above:
Our equation in g, \(g(x)g\left(\frac{1}{x}\right)=1\), can be seen as $$g(x)\cdot\frac{g_r(x)}{x^n}=1$$.Multiplying by \(x^n\) on both sides, $$g(x)g_r(x)=x^n$$
But since \(g\) is a polynomial with degree n, then \(g_r\) can’t have degree higher than 1, if their product is to have the same degree! So all the coefficients of \(g_r\), except the constant term (which corresponds to the leading term of \(g\)), are zero, so that \(g(x)=cx^n\) and \(g_r(x)=c\). Our equation now becomes $$cx^n\cdot c=x^n,$$ from which we conclude that \(c=\pm1\).
And we have solved the problem: \(g(x)=\pm x^n\), and \(f(x)=1\pm x^n\).
There are non-polynomial solutions
How about the non-polynomial case? I now had some ideas, which I couldn’t keep from sharing:
I’ve taken the time to find another solution, to demonstrate that the polynomial really is not the only solution if we drop the requirement that f is a polynomial. It’s interesting, so I’ll show it to you (and to Doctor Rick) though it is far beyond anything you would be asked to do.
What I did was to choose a function g(x) for |x| ≥ 1 such that f(4) = 65, so that g(4) = f(4) – 1 = 64, and also g(1) = 1, so that g(1/1) = 1/g(1). (This makes our function continuous, which seems like a good idea.)
Note that the functional equation implies that \(g(1)=\pm1\), since it must be its own reciprocal. The idea here is to define a piecewise function by choosing a function for the outer part of the domain, and transforming it into a suitable function on the inner part.
We could use almost any function we want; because of the numbers, I chose an exponential function:
A convenient choice was g(x) = 4^(|x|-1). There are infinitely many other possibilities.
For |x| < 1, we take g(x) = 1/g(1/x) = 4^(1-1/|x|). This gives us a piecewise function that satisfies the functional equation g(x) g(1/x) = 1.
From this, we define f(x) = g(x) + 1:
f(x) = { 4^(|x|-1)+1 for |x|≥1, 4^(1-1/|x|)+1 for |x|<1 }
My function is $$f(x)=\begin{cases}4^{|x|-1}+1 & \text{ if } |x|\ge1 \\4^{1-\frac{1}{|x|}}+1 & \text{ if } |x|<1\end{cases}$$
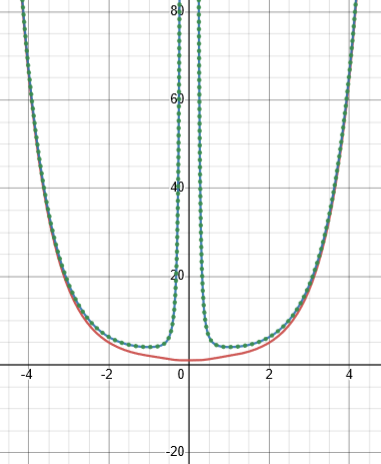
Here is its graph, in red, compared to the polynomial solution, p(x) = 1 + x^3, in black dashes:
Notice that both pass through the three marked points. But f(6) = 1025, compared to p(6) = 217.
So if the problem asked for \(f(6)\) without saying that f is a polynomial, there would not be a unique answer.
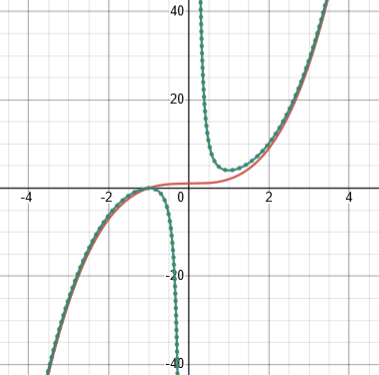
To show that it works, here is a graph showing f(x) f(1/x) in blue and f(x) + f(1/x), in green dots, so you can see they are identical:
The red graph is, again, my function f itself.
Here is the same for the polynomial solution, p(x) = 1 + x^3:
That was a lot of fun!
Both functions satisfy the equation.
Suppose we pick a linear equation for the outer part. Here is the graph of $$f(x)=\begin{cases}\left(21\left(\left|x\right|-1\right)+1\right)+1 & \text{ if } |x|\ge1 \\\frac{1}{21\left(\frac{1}{\left|x\right|}-1\right)+1}+1 & \text{ if } |x|<1\end{cases}$$ in red, together with the LHS and RHS as before:
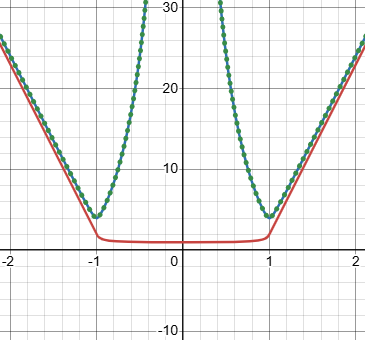
Debarghya closed:
I don’t have enough knowledge about absolute value function or piecewise function. but it is really interesting that there are so many solutions apart from just polynomial functions.
We’d gone well beyond his needs, but demonstrated how interesting a problem can be.