Frequently Questioned Answers: Trisecting an Angle

One of the best ways to get people eager to do something is to tell them it can’t be done. When people who are not well-versed in mathematics learn that it is impossible to trisect an angle with compass and straightedge, they sometimes seem to make it their life goal to “do the impossible”. The result is frequent challenges to that assertion in our FAQ, “Impossible” Geometric Constructions. We’ll look today at several of our attempts to clarify what it means in math to say something is impossible, and to answer those who claim to have done it (people called “trisectors”).

What it is that can’t be done

We’ll start by looking at an early statement of the issue, from 1996:

Trisecting an Angle

I've recently been pondering the possibility of trisecting an angle.  I wasn't sure if it was possible and found a FAQ submitted to you that stated it was indeed impossible.  Has it been proved to be impossible or is it that no one has proved it possible?  The reason I ask is that I think (but am not sure) that I have found a way to trisect an angle.  I am a seventh grade math teacher, so I am not completely ignorant of mathematical proofs.  I would appreciate some information on who would be the best person to contact with my "proof".  I hope you believe me because I think this actually works.

This is the benign species of trisector, one who just isn’t sure what it is that was proved, and isn’t insisting that everyone else is wrong. Doctor Tom answered, presenting the key ideas one by one:

There is, in fact, a proof that a trisection is impossible. Many people think they have found trisections, but they either don't understand exactly what the problem is or their method is flawed.

The problem requires the construction of the trisection using an (unmarked) straightedge and a compass. If, for example, you were allowed to make 2 marks on the straight-edge, there is a trisection.  The straight-edge can only connect points already constructed, or use arbitrary points, and the compass can only be used similarly.

An exact trisection in a finite number of steps is also required since it's easy to do a trisection that doesn't require too much accuracy.  As a limiting case, it might be possible to perfectly trisect an angle in an infinite number of steps.

So what was proved impossible is a specific task using specific methods; if you break the restrictive rule on what tools are available and how they are to be used, trisection is not impossible. For discussions of two such alternative tools, see

Trisecting an Angle: Proof

Trisecting an Angle Using the Conchoid of Nicomedes

(The first of these has a broken link that should now be http://www.faqs.org/faqs/sci-math-faq/trisection/. The second has a link that is now http://www-history.mcs.st-and.ac.uk/history/HistTopics/Trisecting_an_angle.html.)

So how was it proved to be impossible?

The proof that it's impossible basically considers the arithmetic form of the points that can be obtained using a compass and straight-edge.  In a sense, they are "quadratic" devices - the new points generated are solutions of quadratic equations of previously constructed points.

So you can clearly get things like square roots, fourth roots, eighth roots, and so on (and it's a bit more complicated than that - what you can get are field extensions of degree 2 over whatever you begin with). But you CANNOT solve irreducible cubic equations this way - such solutions require extensions of degree 3, and no combination of multiples of 2 gives a multiple of 3 (to put it in an inexact, but hopefully clear, way).

You can, beginning from nothing, construct a 60 degree angle. So if you can trisect anything, you can trisect the 60 degree angle which you produce. So if you have a trisection, you can construct, from scratch, a 20 degree angle. Hence you can construct the sine and cosine of 20 degrees.  But it's easy to show that the sine and cosine of 20 degrees are roots of an irreducible cubic equation over the rational numbers.  This is a contradiction, so a trisection is impossible.

To get the details, read about fields and field extensions in an abstract algebra book.

One excuse many trisectors give for doubting the proof is that they think algebra can say nothing about geometry. But it can!

As for this teacher’s claimed trisection,

So the bottom line is, there's probably something wrong with your trisection, not because I've seen it, but because I've studied field extensions and irreducibility.

That idea, “I know it’s wrong without needing to see it,” angers a lot of people; but that’s how math works!

The start of an obsession

Here’s another trisection attempt of the relatively benign variety, from 1999:

Attempt at Trisecting an Angle

We have a bisector of an angle of 30 degrees (or any degree) that extends into the angle 1" and extends outside the angle 2". Then we have bisector line 3" long. From the vertex of the angle, a circle with a 1" radius is drawn. Then 2" outside the angle, and on the bisector, a circle with a 3" radius is drawn. The two circles meet on the bisector of the angle 1" inside the angle. 

Question: Are the arcs of the two circles within the angle the same length?

Arc a-b of small circle = arc A-B of larger circle.

Both arcs are 1" within the angle.

Hollis doesn’t come right out and say he’s doing the impossible; here is a picture of his work, so you can see what he is doing (using A₁, B₁, A₂, B₂ for his a, b, A, B):

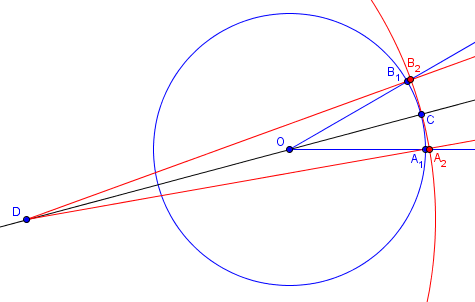
I responded first by noting that the arcs are not, in fact, the same length, and observing that if they were, he would have trisected angle A₁OB₁:

I could show you the trig to work out the actual arc lengths, but it's pretty ugly and probably not worth the effort. I'll just tell you they are not the same.

Your construction is reminiscent of some attempts I've seen to trisect an angle. In particular, the figure looks much like Archimedes' method, which requires a marked straightedge, and that in itself is enough to tell me that the answer will be no. If the arcs were the same, then the angles would be in a 3:1 ratio (since they have the same arc length and the radii are in 3:1 ratio), and you would have trisected the angle; since I know that's impossible with a construction that can be done with compass and straightedge, I don't really have to do the extra work.

I tried to encourage him to do math, without the aim of trisecting an angle:

If that's what you're trying to do, don't feel it's foolish to try. As the alchemists discovered useful things in the process of trying to do the impossible, you may learn a lot about what does work in trying to do what won't. There are some fascinating ways to trisect an angle using special tools, as our FAQ tells you if you dig deep enough, ... and the attempt to prove that any given method might work can help you get a better feel for geometry, and stretch your mind considerably. What you'll want to do, though, is to develop the skills to prove for yourself whether something is true, rather than make a conjecture and have to ask whether it is true. That's the fun part of geometry, and what makes it more challenging than any other part of elementary math.

Hollis wrote to us periodically over the following years, sometimes with questions that I answered with comments like, “This looks suspiciously like an attempt to trisect an angle, which of course can’t be done (exactly) with compass and straightedge. Can you tell me what you are doing?” Eventually, he explicitly became a serial trisector, immune to whatever we tried to say.

The burden of proof

Here is a trisection attempt that turned out to be interesting:

Trisecting an Angle

I've been looking for someone to talk to about the trisecting an angle problem from ancient Greece. I understand the whole modern algebra proof thing but it doesn't disprove the possibility of angle trisection. At least not from the way I have read it and understood it. I came up with a method when I was 16 and in geometry class and so far no one can disprove it. I tried proving it geometrically for a while but gave up. All I know is that with best drawing programs using only circles and unmeasured lines, it works at least to the naked eye for any angle from 5 to 175 degrees. I've done numerous examples trying to find one where it is off by more than the error when using a compass and so far everything I've done is a perfect trisection. Who can I show this to? I think I have something here...

Eric clearly doesn’t understand that algebra did prove that trisection (by the rules) is impossible; and that his attempt can’t be called exact until it is proved to be exact — the burden of proof is on him to prove it, not on others to disprove it! But I asked him to show his work, and (in a discussion too long to include here) discovered that it could be made exact if only you could adjust a center point so that other points coincide with a circle. This makes it like a marked-straightedge construction.

Unfortunately, this page got me started on a side career of making similar checks of approximate trisections.

Why your trisection isn’t valid

A 2001 question from Joe provided a perfect opportunity to discuss what people are misunderstanding when they think they have a trisection. It started innocently, as many do:

Angle Trisection: Construction vs. Drawing

Has anyone ever divided an angle into three equal parts by construction? I have been told it has not been accomplished.

Note that Joe interprets the claim that it can’t be done as a mere challenge, that no one has yet done it. This is what drives trisection mania.

Doctor Tom replied:

Using the standard methods of construction with a straightedge and compass, it can be proven that it is impossible to trisect an arbitrary angle.

People who think they have solved the problem usually make one of two mistakes:

1) They trisect a particular angle that happens to allow a trisection. For example, anyone can trisect a 90-degree angle.

2) They do not understand the "rules" of straightedge and compass construction. For example, if you are allowed to make two marks on the straightedge to turn it into a sort of ruler, you can trisect any angle. But the official rules do not allow this.

We have had a number of claims related to specific angles; here is one:

Trisecting a Right Angle

Others start with a known angle, such as Hollis’ 30°, just as an example, but apparently thinking that measuring their result as 10° will constitute proof.

But Joe turned out to be a serious trisector, as he replied:

I have trisected arbitrary angles up to 90 degrees. Don't laugh until you see it. Only a straightedge and a compass. No measuring. The drawing must be precise for the angle to be correct. Where could I submit my effort for confirmation?

So he claimed to satisfy the requirements, but something he said suggested the need to add another clarification, so I replied:

I notice something in what you just said that indicates where you are misunderstanding the trisection problem. Dr. Tom listed two mistakes people commonly make (trisecting only a specific angle, or using the wrong tools). But there is another that is even more common: not recognizing what we mean by an exact trisection.

When you say that "the drawing must be precise," you show that it is the drawing itself that you have been focusing on. But to a mathematician, the drawing itself is nothing. It is only a representation of something that really happens in an ideal world where lines have no thickness, and so on. In that world, we can prove that a construction is ABSOLUTELY exact; either it meets the precise point you claim, or it is a false construction. And since this is the world of the mind, ONLY proofs count. It doesn't matter how good a drawing you make, it proves nothing.

Every trisector we have heard from has made a claim without proof, depending only on how things look. (Some, after reading this page, have made attempts at proof, but they generally have no idea what a real proof looks like; otherwise, they would have understood that what is proved impossible really can’t be done.) But no measurements of a physical drawing can be accurate enough; whereas when you do a proof, there is no need to have an accurate drawing.

So unless you can prove that your construction really works exactly, you have nothing to show anyone. And we know that you can't, because it has been PROVEN that such a construction can't be done.

I've seen many constructions that come remarkably close, usually just because they are very complex; there is nothing at all impressive about a close approximation. Please don't waste your time on this, as so many people have.

Perseverance

Unfortunately, the discussion didn’t end here; the next month, Joe wrote back telling us about his constructions, each of which assumed something that is not true about chords and arcs (see below on that). And in 2004 he wrote again:

Trisecting an Angle Using Compass and Straightedge

There, he asked me to analyze his construction on Geometer’s Sketchpad (similar to the current GeoGebra), which I had used on Eric’s construction that I mentioned above; I had to tell him that not only physical measurements, but also calculations (necessarily rounded) by a program do not constitute proof. I did analyze it, to show him that it was not exact, but also demonstrated what a proof looks like, giving a proof of an angle bisection for comparison. At the end, I added, referring to the FAQ:

As that explains, it has been proved to be impossible to exactly trisect any arbitrary angle using only compass and unmarked straightedge; and as I pointed out, "exact" to a mathematician means something entirely different from "as close as you can measure"; it means "provably exact".

"Impossible" is a common thing in math.  For example, it is impossible to find two odd numbers whose sum is odd; it is easy to prove that the sum of two odd numbers is always even, so we just accept that.  I've never heard of people who, when told this fact, spend their lives trying to find two odd numbers whose sum is odd; but there have been thousands of people who have wasted a lot of time trying to find a way to trisect an angle.  Most of them probably have no idea that a valid trisection is not just a drawing but a proof!  They just hear that it can't be done, don't understand how that could be proved, and decide to show that it doesn't apply to them.  Since it's not as obvious as adding odd numbers, they never realize how silly what they are doing is.

To keep your mind alert, I would suggest something more "constructive" than trying to do what has been proved impossible.  Take some time to learn the basics of geometric construction and proof, then work through the exercises in a good book on the subject, which will ask you to do constructions that are hard but possible.  That way you are giving yourself a major mental challenge, but one that you can really master with effort.  It's a lot more rewarding!

I have said this sort of thing to several others I have corresponded with. This discussion continued a little further, and ended with his saying, “I will put your note about proof under the glass on my desk as a reminder to leave the trisect impossibility alone.”

But, alas, he wrote again in 2009, with yet another attempt. It turned out not to be close at all. He hadn’t learned a thing.

Trisecting a chord doesn’t trisect the angle

Let’s look at one more page: a proof that a common assumption of trisectors is false:

Trisecting an Angle and the Opposite Side in a Triangle

Prove that it is impossible to have a triangle in which the trisectors of an angle also trisect the opposite side.

I am unsure how to prove this. It seems that if i trisect the angles of an equilateral triangle so that each of the trisected angles is 20, it would indeed divide the opposite side into 3 equal pieces.

I have completed geometry, and I have tried several things. I got started trying to use exterior angle theorem, but got confused. I think that may be a good way to do it, but I dead ended after extending two of the sides to create isosceles triangles. I think it may be all of the criss-crossing lines that is getting me confused.

I replied to this refreshing question:

I don't think I've ever tried proving this, but it's a very nice 
little theorem!

It may seem as if trisecting an angle in an equilateral triangle would
work, but it is not true.

I think I'd approach it by contradiction.  Suppose that you have a 
triangle ABC with trisectors BD and BE, D and E being on AC, and 
further suppose that D and E trisect AC, so that AD = DE = EC:


Now focus on triangle ABE.  Here BD bisects angle ABE, while D is the 
midpoint of AE; so BD is both an angle bisector and a median.  What 
does that imply?  Repeat with triangle DBC, and look for a 
contradiction.

There may be many other ways to approach this, so if you see any 
ideas of your own while you try this out, go ahead and pursue them!

The implication I had in mind is that triangle ABE must be isosceles, because triangles ABD and EBD are congruent. It also implies that BD is perpendicular to AC. Since the same must be true of triangle DBC, this triangle can’t exist.

In summary, here is what I wrote to someone who wrote in 2009, starting out “Why do you print false information on your site?”:

It has been proved that you can't construct a provably exact trisection of an arbitrary angle using the classical rules (only a compass and unmarked straightedge, in a finite number of steps). People who claim they can, generally don't really have a provable trisection, or are bending the rules in some way without realizing it. ... If you have no proof to show me, then you have not met the requirements of a valid construction, and most likely it is just measurably close, not mathematically exact. The imprecision of physical tools has nothing to do with it, because we do not demonstrate the correctness of a construction by doing it physically and seeing that it looks as close as our tools can make it. The tools we really care about are all in the mind, and that is where the proof has to be done.