Last time we looked at the meaning of the concept of locus. This time, we’ll explore seven examples, from two students. We’ll look at both algebraic (equation) and geometric (description) perspectives.
Five examples in a plane
Here are some examples, from 1999:
Locus and Equations of Lines I'm currently trying to help my niece who is in 10th grade with locus and line equations. The concept isn't coming back to me. She has the following homework: Describe the locus of points that are 3 units from the line x = -1 and give the equation of the locus. Describe the locus of points that are 6 units from the point (3,-1) and give the equation of the locus. Describe the locus of points equidistant from the x and y axis and give the equation. Describe the locus of points equidistant from the points F (-2,1) and G (6,3) and give the equation. Describe the locus of points equidistant from lines y = 4 and y = -2 and give the equation of the line. We can graph the points on the x and y axis but we don't understand how to find the locus of points. We know the formulas for slope, the line equation, and the distance formula, but when do you use each? What is the process for these problems so I can explain them to her? Thank you for your help. Marguerite
Since the goal here is to write both descriptions (in words) and equations, we are going a little beyond the questions last time, though it is really the same concept.
I answered:
Hi, Marguerite. The basic concept of a locus in geometry is very closely related to that of an equation in algebra. We want to describe all points that satisfy some condition, by choosing an unknown point (x, y) and seeing what it means, algebraically, to satisfy the condition.
Recall that a locus is a set of points, thought of as a single entity. The graph of an equation is the set of all points represented by ordered pairs that satisfy the equation; so the equation is just a way to describe symbolically the condition for the locus, and its graph is the locus. We are to describe each locus both in words and as an equation.
In my reply, I led Marguerite close to the answers, but left her some thinking to do. Here, we’ll finish them up.
1: Fixed distance from a line
Let's look at your problems one at a time.
1. Describe the locus of points that are 3 units from the line x = -1 and give the equation of the locus.
Pick any point (x, y). What does it mean to be 3 units from the line x = -1? Since this is a vertical line, the distance is just the horizontal distance from x to -1:
^ ^
| |
| y+ *(x,y)
| |
| |
| |
----------+---+-------+--
-1| 0| x
| |
| |
|<--------->| d=|x-(-1)|
(We use the absolute value because x could be on either side of -1.)
So the equation of the locus is:
|x - (-1)| = 3
We’ve translated the condition given in words into an equation.
Here is a typical point shown above, 3 units to the right of the blue line:
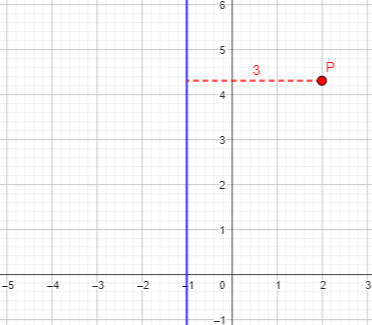
But the point could also be to the left:
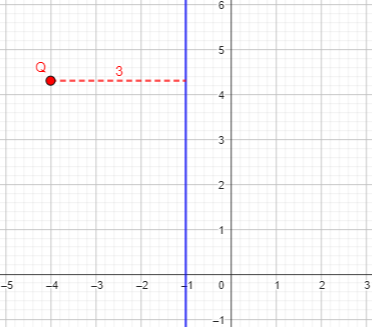
Recall the comment last time that a locus must consist of all such points, and only such points; if we’d omitted the absolute value, we wouldn’t have the entire locus:
Every point that is 3 units from the line satisfies this equation, and every point that satisfies this equation is 3 units from the line. So this is the locus we are looking for. (Incidentally, don't worry that y isn't in this equation - that's how vertical lines work.) Can you see what this locus is geometrically? Think in terms of parallel lines, and remember what I said about being on either side! The equation can be rewritten as two equations, in the form "x = this OR x = that."
The equation can be written as \(|x+1|=3\); this means that \(x+1\) must be either \(3\) or \(-3\). And the equations \(x+1=3\) and \(x+1=-3\) are equivalent to $$x=2\text{ or }x=-4$$ So here is our locus, \(|x+1|=3\), consisting of two parallel lines:
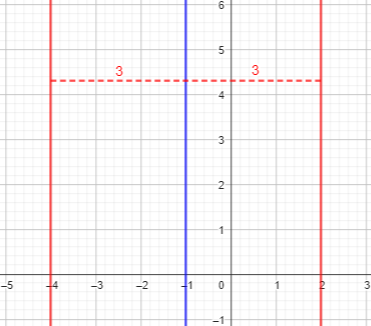
Last time we saw a circle as the locus of a dog tethered to a stake; this is the locus of a dog tethered to a “zip line”! It’s a pair of lines parallel to the given line, one on each side of it.
2: Fixed distance from a point
2. Describe the locus of points that are 6 units from the point (3,-1) and give the equation of the locus. This is similar, except here the distance formula you want will be the Pythagorean theorem. Write an expression for the distance of point (x, y) from (3, -1), and set it equal to 6 to make the equation of the locus. To describe the locus, think about how you would draw it, by making a string of length 6 and tacking one end of it at (3, -1). Where can the other end be? Could you also draw this with a compass?
Here is a point 6 units from \(3, -1)\):
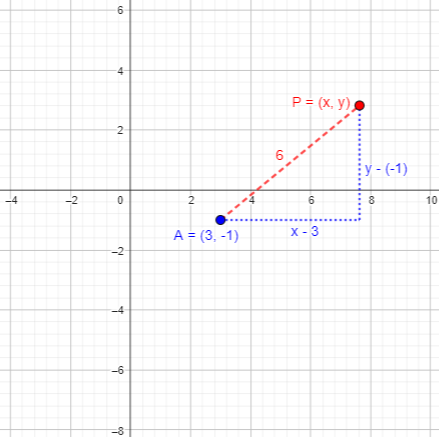
We want an equation that will be true whenever a point \((x,y)\) is a distance of 6 units from \((3,-1)\). The distance d between two points \((x_1,y_1)\) and \((x_2,y_2)\) satisfies \(d^2=(x_2-x_1)^2+(y_2-y_1)^2\), so our locus is defined by $$(x-3)^2+(y-(-1))^2=6^2$$ which we can simplify to $$(x-3)^2+(y+1)^2=36$$ What shape is it? A circle with center \((3,-1)\) and radius 6:
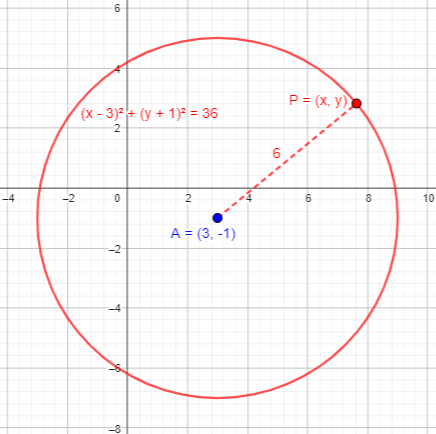
We saw this idea, last time – but without the equation.
3: Equidistant from two perpendicular lines
3. Describe the locus of points equidistant from the x and y axis and give the equation. This requires two expressions: one for the distance of point (x, y) from the x axis, and one for the distance from the y axis. Those are pretty simple, but remember those absolute values! Now set them equal, and you have an equation describing all points for which the two distances are equal, which is your locus. To describe this, either look at the equation in terms of quadrants, or think geometrically about angle bisectors.
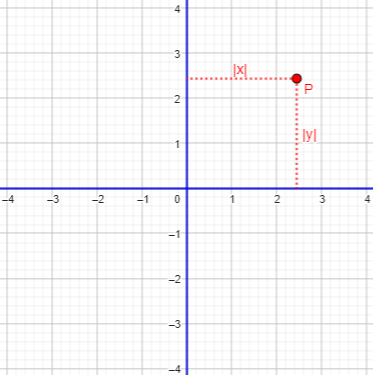
The distance of a point \(P(x,y)\) from the x axis is \(|y|\); the distance from the y axis is \(|x|\):
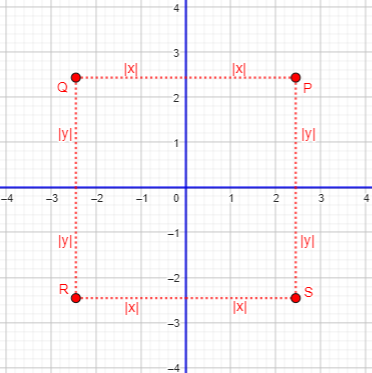
But either x or y can be negative, so we have to be careful not to ignore points in other quadrants:
So the equation of our locus is \(|y|=|x|\). But what does that look like? Algebraically, we can rewrite it as \(y=\pm|x|\), and since this means to remove the sign from x and then put either sign back on, it is merely \(y=\pm x\). This is a pair of lines, \(y=x\) and \(y=-x\):
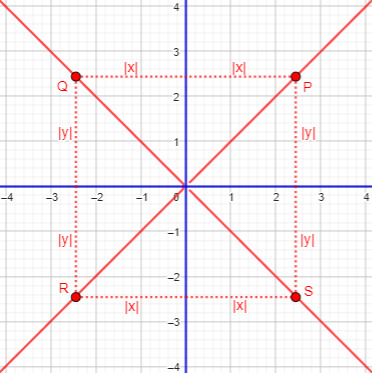
What we’ve done here is to bisect all four angles at the origin (because the congruent right triangles shown imply congruent angles).
4: Equidistant from two points
4. Describe the locus of points equidistant from the points F (-2,1) and G (6,3) and give the equation. Again, write an expression for the distance of (x, y) from (-2, 1), and one for the distance of (x, y) from (6, 3), and set them equal. You can simplify this equation quite a lot; squaring both sides will be the first step.
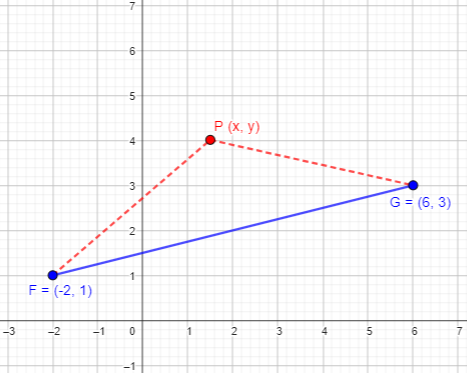
The two distances are \(\sqrt{x+2)^2+(y-1)^2}\) and \(\sqrt{(x-6)^2+(y-3)^2}\). Setting them equal, and then squaring, we get $$\sqrt{(x+2)^2+(y-1)^2}=\sqrt{x-6)^2+(y-3)^2}\\(x+2)^2+(y-1)^2=(x-6)^2+(y-3)^2\\x^2+4x+4+y^2-2y+4=x^2-12x+36+y^2-6y+9\\16x+4y=40\\4x+y=10$$
That looked bad at first, but worked out nicely. It is clearly a line, and we’ll see in a moment that it is just the line it needs to be.
You may prefer to do the hard work in geometry rather than algebra. There is a theorem that tells you that the locus of points equidistant from two points is the perpendicular bisector of the segment they define. You will have to find the coordinates of the midpoint of this segment (think of averaging their coordinates), and write the equation of the line through this point perpendicular to the segment (the slope of this line will be the negative reciprocal of the slope between the two points).
This theorem was mentioned last time.
The slope of line FG is \(\frac{1}{4}\); the midpoint M is \((\frac{-2+6}{2},\frac{1+3}{2})=(2,2)\). The slope of the perpendicular line is \(-4\), so the equation of the line is \(y-2=-4(x-2)\), which simplifies to \(4x+y=10\), the same answer as before.
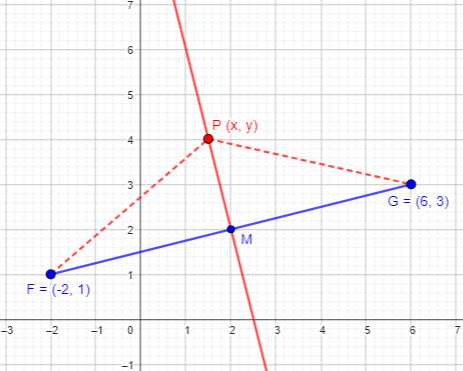
You can prove that the line is perpendicular by considering congruent triangles PFM and PGM.
It's fun to do this both ways and see that geometry and algebra agree! But it does take some work either way.
5: Equidistant from two parallel lines
5. Describe the locus of points equidistant from lines y = 4 and y = -2 and give the equation of the line. Now we're back to something like the first problem. Write expressions for the distance of (x, y) from each line, and set them equal. The absolute values get in the way, but if you think carefully you can simplify this into the equation for a single line. You may be able to avoid the absolute values entirely if you think about what is happening geometrically first. Where can a point be if it is the same distance from two parallel lines?
This is like the first example we saw last time, except that we need to give an equation.
Here are the two lines:
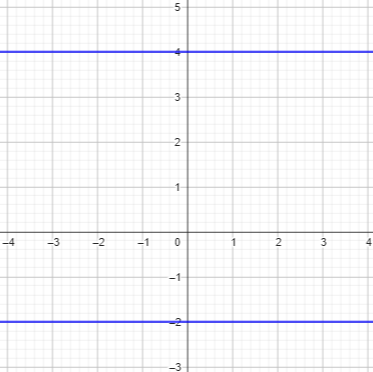
Here is a point equidistant from them:
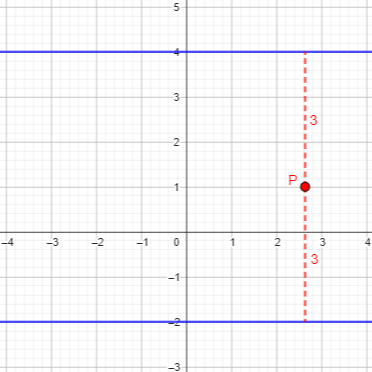
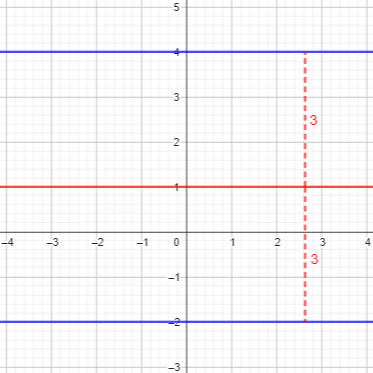
The distance from \(P(x,y)\) to \(y=-2\) is \(|y-(-2)|\); the distance from \(P(x,y)\) to \(y=4\) is \(|y-4|\). So our equation is $$|y+2|=|y-4|$$
One way to solve this is to observe that the absolute values change behavior when \(y=-2\) and when \(y=4\), so we can consider three cases: $$y\ge4: y+2=y-4\Rightarrow 2=-4\text{ (impossible)}\\
-2<y<4: y+2=-(y-4)\Rightarrow 2y=2\Rightarrow y=1\\
y\le-2: -(y+2)=-(y-4)\Rightarrow -2=4\text{ (impossible)}$$
So the equation of the locus is simply \(y=1\). This is just the average of the two y-coordinates, which makes sense: The locus is the parallel line halfway between the given lines:
I hope these examples demonstrate the meaning of locus and the methods that can be used to find the equation. If you need more, try searching for the word "locus" in our archives. If some of my specific steps didn't make sense, or I went too fast, write back and I'll try again.
Two more examples, in a plane and in space
A 2008 question takes us deeper into the process, with harder examples:
Drawing a Locus of Points I was doing my geometry homework, and some of the questions are rather difficult and some are easy. For example: All points in the plane that are equidistant from the rays of an angle and equidistant from two points on one side of the angle. The directions say to drew a diagram to find the locus of points that satisfy the conditions. I got the first part before the word "and." My drawing: / / / /_______ Okay, so there's the angle, and then I drew in an angle bisector which I was unable to do on here.
(I’ll hold onto the rest of the question, which includes another example and a general question, until later.)
1: Equidistant from two rays and two points
This is, indeed, a trickier question, because it combines two separate conditions. Erin knows the first: The locus of points equidistant from two rays is the angle bisector. (We touched on this in example 3 above.)
I answered:
Hi, Erin. You've asked a big question; but let's see if I can help one part at a time, then come to some broader conclusions. You are given two conditions: A: equidistant from the rays (sides) of the angle B: equidistant from two (given) points on one side (ray) To find all points that satisfy BOTH A and B, you can draw each locus (A and B) separately, and the intersection of those will be your combined locus--the only point(s) for which both A and B are true.
A point that satisfies the conditions for two loci is in their intersection.
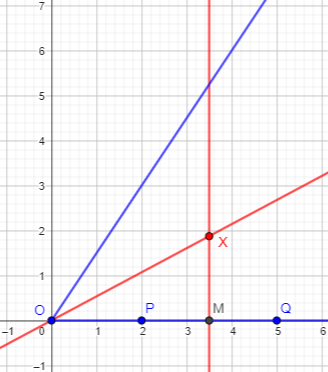
You've drawn locus A, a ray from the vertex. Now let's add in two given points on the horizontal side:
/
/
/
/
/ / <--- locus A
/ /
/ /
/ /
O-----P-------Q---
What is the locus B, the points that are the same distance from P as from Q? You're probably as familiar with this one as with the angle bisector. Draw it, and where that line crosses locus A is the single point in the locus "A and B".
This is what we saw in example 4 above: the perpendicular bisector of segment PQ. So the solution will the intersection of the two lines, which is a single point. Here is an example:
This would be harder to assign as an algebraic problem, because finding the equation of the angle bisector requires either trigonometry or harder algebra. Give it a try if you like.
2: Equidistant from two intersecting planes
Here is part 2 of the question, which is our first (and only) problem in space rather than on a plane:
Another problem I had trouble with was:
All points in space equidistant from two intersecting planes.
I drew two planes intersecting perpendicularly just to make it easier to visualize.
______
| |
___o | |o____
| | | |
|____| |____|
o |____|o
The dots are the four points equidistant from each of the planes, but the book shows that where the dots are, are two other planes that intersect each other. And the four planes intersect at one point.
The idea of four points suggests that Erin is visualizing this at least a little correctly.
I answered:
It can be quite difficult to draw something like this in the first place; I wouldn't say that your planes look like they intersect, but perhaps you can visualize what you have in mind anyway. Here's how I might draw it (the best I can in plain text, and I'm pretty much an expert at it!):
+
/|
/ |
+ |
| |
+------| +--------+
/ | /: /
/ |/ : /
+---------+--------+
| |
| +
| /
|/
+
I drew the planes so they look perpendicular, which they will not generally be; but it's hard enough to draw them this way!
Some geometry classes spend a little time learning to draw 3D figures like this; probably most don’t! I gave a little lesson here. It might be easier to make a physical model using sheets of cardboard – or just pages in a book!
Now, where can you be and be the same distance from both planes? The situation is much like the angle bisector of an angle in a plane; in fact, this figure represents a "dihedral angle" (between two planes). A side view (still making them look perpendicular) would be:
^
. | .
. | .
. | .
. | .
<---------+-------->
. | .
. | .
. | .
. | .
v
The two dotted lines represent all points in the plane that are equidistant from the two solid lines.
This looks like our example 3 above.
Now imagine this as just a side view of the planes; the dotted lines, too, are side views of planes, which pass through the same line of intersection. I'll just barely try to draw this:
+
. /| .
. . / | ..
. .+ | . .
. | | . .
+.-----| +--.-----+
/ . | /:. /
/ . |/.: /
+---------+--------+
. . | .| .
. . | +. .
.. | / . .
. |/ .
+
Note that, since it's hard both to draw and to visualize three dimensions, I used two dimensions in two ways: first, using an ANALOGUE (intersecting lines in a plane are LIKE intersecting planes in space, so they give a sense of what the result might be like); and second, using a SIDE VIEW (or cross section) in order to draw part of what I'm imagining, still keeping things simpler than trying to picture the whole thing. We do the same thing to try to visualize four-dimensional objects, which is quite a trick!
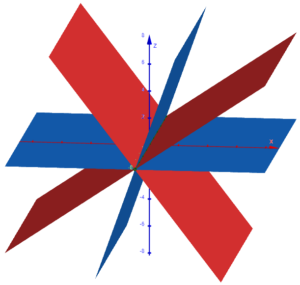
Here is a version of the graphs above, from GeoGebra:

As in other figures, the blue planes are the given, and the red planes are the locus. But with software, we don’t need to start with perpendicular planes. Here is an example where they are not:
Thinking about thinking about the problem
She closed with some general questions:
I think my major problem with these locus problems, is reading the problem. I just don't think I understand what I'm reading, or I may understand part of it and when the second part comes, I don't know what to do. I think I'm having problems channeling all the information it gives, so I try to break it up. When I break it up, I sometimes have problems putting it together. My teacher told me to split the problem into two, like do the first part before "and" then do the second part, which would be after "and." He also told us to draw the given in one color, then the points or whatever it is that the problem says in another color, so where the non-given things that meet is what we describe.
I answered the first paragraph:
That's not a bad analysis. Reading mathematicians' twisted grammar just takes time and experience! A big part of math is being able to break a large problem into pieces, and then be able to put them back together. Often that skill is developed by being even more orderly than you need to be once you understand the topic more fully; you may need to write down more of what you are doing (sort of like making notes to yourself to remind yourself where you left your glasses when you took them off, so you can find them again later). For example, I gave names to the two parts, A and B, so I could clearly communicate with myself (and you) about those parts. I first summarized the overall strategy (draw A, draw B, intersect), and then filled in the outline. Such self-communication (naming things and writing down what they mean) and organization (outlining a plan before doing it) is very helpful. You won't always see ahead of time what all the steps will be, but you can at least keep good records of what you have done while you explore. Think of yourself as Lewis and Clark, not knowing just how they'd get to the Pacific, but making their own maps so they'd know where they'd been once they found where they were! Problem-solving in general requires that sort of skill. But I'm digressing...
We’ve talked about similar problem-solving ideas in How Can I Stop Making Careless Mistakes?
As to the teacher’s ideas in the second paragraph:
All of that is good advice. (I used dotted lines for a similar purpose.) It just takes time and practice to make it all work!
Erin wrote back:
Thank you very much for answering my question. I understand it better, and I think I'll do more problems over the weekend and try to get better at it. Thanks for the Lewis and Clark advice and organization advice. I'll start being more organized again. I think organization helps a lot in math! Thanks again!
