Square roots commonly are irrational numbers, so that it is necessary to estimate them. Usually today, we use a calculator to find them. Many students, however, are curious about how they could do it without a calculator. Here I want to reverse the usual format of this blog, presenting a summary I have written that compares three main methods you could use, and just giving references to our various discussions of them.
Two of these methods, Binary Search and Newton’s Method, were discussed in their more general form last week when we discussed numerical methods of approximation. I also showed a student’s discovery of linear interpolation for finding square roots.
Guess-and-check (High/Low Method, Binary Search)
The simplest thing to do is just to guess a square root, check it by squaring, and then make a new guess, higher or lower, based on the new information you have, but still within known bounds. This is not mere random guessing, but orderly guessing!
The key idea is that if \(a^2 < n < b^2\), then \(a < \sqrt{n} < b\). For example, since 20 is between 16 (\(4^2\)) and 25 (\(5^2\)), its square root must be between 4 and 5.
Here are the steps to estimate the square root of a number n:
-
- Find a perfect square near n, and use its square root x as your first guess.
- If \(x^2 > n\), make a new guess lower than x; if \(x^2 < n\), make a new guess higher than x.
- Keep repeating step 2, trying whole numbers until you find a pair of consecutive integers that surround the square root; then try tenths, then hundredths, as far as you want. Use your number sense to choose whether to take small or large steps.
Example 1: Estimate the square root of 683 to the nearest tenth by guess-and-check.
We first look for two consecutive perfect squares that 683 is between:
We know that \(20^2=400\) and \(30^2=900\), so \(\sqrt{683}\) must be between 20 and 30.
Try 25: \(25^2=625\) which is less than 683, so the square root is greater than 25.
Try 26: \(26^2=676\) which is less than 683, so the square root is greater than 26.
Try 27: \(27^2=729\) which is greater than 683, so \(\sqrt{683}\) is between 26 and 27.
Now we look for the tenths that \(\sqrt{683}\) lies between:
Since 683 is considerably closer to \(26^2\) than to \(27^2\), we should start on the low side.
Try 26.2: \(26.2^2=686.44\), which is high, so our square root is a little lower than 26.2.
Try 26.1: \(26.1^2=681.21\), which is smaller than 683, so we know that \(\sqrt{683}\) is between 26.1 and 26.2.
To make the final decision which is closer, we can check the number halfway between, 26.15:
\(26.15^2=683.8225\) which is high, so we know that \(\sqrt{683}\) is closer to 26.1.
Here is one way to record our work, listing tens, then ones, then tenths and marking which our root is between:
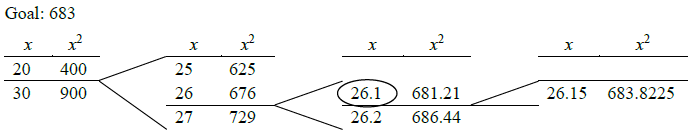
The circled number is our answer. A calculator shows that \(\sqrt{683}=26.134268…\), so this is a good estimate.
The main difficulty with this method is that it may take several tries to get each decimal place; but the only arithmetic we have to do is multiplication, which can be done by hand without much trouble.
This sort of trial-and-error, and the closely related method of binary search, are described here:
What is the Square Root of 8? (Doctor Tom, 1996) Finding square roots (Doctor Dave, 1996; Doctor Jerry, next method) Method to Find Square Root of Pi (Doctor Steve, 1997: binary search)
Divide-and-average (Babylonian Method, Heron’s Method, Newton’s Method)
This ancient method is similar, in that we make a series of approximations, but this time we don’t merely guess; a formula tells us what number to use next. It is based on the fact that if \(ab=n\) and \(a\) is less than \(\sqrt{n}\), then \(b\) has to be greater than \(\sqrt{n}\). So if we start with a guess \(x\) that is on one side of \(\sqrt{n}\), then \(\frac{n}{x}\) will be on the other side of \(\sqrt{n}\), and their average will be closer to \(\sqrt{n}\). Here is the method:
- Find a perfect square \(x^2\) near \(n\), and use its square root \(x\) as your first guess.
- Calculate \(\displaystyle\frac{x+\frac{n}{x}}{2}\) and use this as the next guess.
- Keep repeating the process in step 2, until the difference between one guess and the next is as small as you want. The exact root is always between one guess and the next.
Example 2: Estimate the square root of 683 to the nearest tenth by divide-and-average.
Since, as before, \(\sqrt{683}\) is between 20 and 30, let’s start with 25.
The next guess is \(\displaystyle\frac{25+\frac{683}{25}}{2}=\frac{25+27.32}{2}=26.16\).
The next is \(\displaystyle\frac{26.16+\frac{683}{26.16}}{2}=\frac{26.16+26.109}{2}=26.135\). (I am rounding to 3 decimal places.)
These are the same in the tenths place, so our answer is 26.1.
Here is one way to record our work:
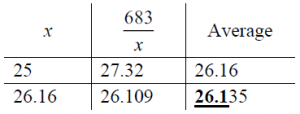
The trouble with this method is that we have to divide by numbers with many decimal places, rather than merely multiply. To do it by hand, you have to decide ahead of time how many decimal places to use — I recommend rounding to two places beyond your goal, as I did above (three places). On the other hand, this method improves its estimate very fast, doubling the number of correct digits at each step. If your original guess has 1 digit correct, in two steps you will have about 4 correct digits, as in this example.
Another problem is that this method theoretically keeps going forever, even if the answer can be written exactly; it gets closer to the exact value, but can never reach it. Commonly, however, it will stop because of rounding, and you can tell that you have the exact answer. Here is an example:
Example 3: Estimate the square root of 68.89 to the nearest tenth.
Since 68.89 is between 64 and 81, let’s start with 8.
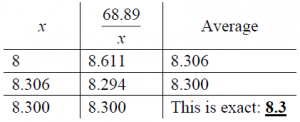
The method is actually a special case of Newton’s method for approximating a zero of any function, applied to the function \(f(x) = x^2 – n\). Newton’s method is based on calculus; from a first guess, it makes a succession of guesses calculated as \(\displaystyle x_1 = x_0 – \frac{f(x_0)}{f'(x_0)}\), where \(f’\) is the derivative of \(f\). In our case, \(f'(x) = 2x\), so the formula gives \(\displaystyle x_1 = x_0 – \frac{x_0^2 – n}{2x_0} = \frac{x_0^2 + n}{2x_0} = \frac{x_0 + \frac{n}{x_0}}{2}\).
This method was described here:
Square roots by hand: Divide and Average (Doctor Jerry, 1996) Square Roots: Estimate, Divide, Average (Doctor Mitteldorf, 1997, also longhand) Newton's Method and Square Roots (Doctor Jerry, 1998, Newton's method) Heron's Method for Finding Square Roots by Hand (Doctor Paul, 2001, also guess-and-check)
It is extended to higher roots here:
Cube roots (Doctor Jerry, 1997) Calculating 4th Roots, 5th Roots... (Doctor Jerry, 1999) Formula for Finding Mth Root (Doctor Rob, 2001; Doctor Jacques, 2004)
It is also the primary method taught in our FAQ on the topic:
Square Roots Without a Calculator
Digit-by-digit (Longhand or Long Division Method)
This method is very different from the others. It looks like long division, and gives us the answer exactly, one digit at a time. However, it requires skill to guess each digit efficiently. Here is the method:
- Write the digits of the number in pairs, going both left and right from the decimal point. One digit of the root will be written above each pair, and the decimal point will be above the decimal point in the radicand. We will ignore the decimal point in all work.
- The first digit of the root is the largest number whose square is less than the first pair. Write it above that pair. Square this digit, and subtract that from the first pair.
- Bring down the next pair of digits, producing the number you will now work on.
- Double the current value of the root and put a blank to the right of it. Now find (by trial and error) a digit x to put in the blank so that the resulting number, times x, will be as large as possible without exceeding the number being worked on. You can make a first guess by division.
- Write this digit x above the last pair brought down, and subtract the product from the number being worked on. Go back to step 3, and repeat for the next digit.
Example 4: Calculate the square root of 683 to the nearest tenth by longhand.
 |
Start at the decimal point and make pairs of digits (including one pair of zeros to the right to make room for tenths in the answer). |
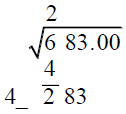 |
The first digit is 2 because \(2^2\) is the greatest perfect square less than 6.
Subtract \(2^2=4\) from 2, and bring down the next pair. We’re working on 283. Double the root we have so far, 2, to get 4, and write a blank next to it. |
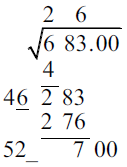 |
Our goal is to fill that blank so that \(4\_\cdot\_\le 283\), as close as possible.
For a first guess, we can divide 283 by 40, which gives about 7. Trying 7 gives \(4\underline{7}\cdot \underline{7} = 329\), which is too big. For a next try, divide 283 by 47, which is about 6 (or just subtract 1 from the first guess). We find that \(4\underline{6}\cdot 6 = 276\), which is just a bit less than 283, so we use 6. Write 6 in the answer, and subtract 276 from 283. Bring down the next pair. Double the root we have so far, 26, to get 52, and write a blank next to it. |
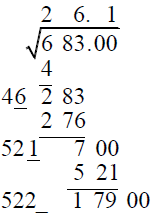 |
Now we want to fill this blank so that \(52\_\cdot\_\le 700\).
The obvious answer is 1: \(52\underline{1}\cdot \underline{1} = 521\). Put 1 in the answer (after the decimal point), and subtract 521 from 700. We now have a square root accurate to the tenths place; if we want to round to the nearest tenth, we can test to see whether the next digit is 5 or more: \(522\underline{5}\cdot \underline{5} = 26125\) is too large, so the next digit is less than 5 and we don’t have to round up. |
This method is based on the fact that \((10a+b)^2 = 100a^2 + 20ab + b^2 = (10a)^2 + (20a+b)b\). For a detailed explanation of the reasoning, see
Finding Square Roots (Doctor Peterson, 1998)
Example 5: Calculate the square root of 68.89 exactly. (Compare Example 3 above.)
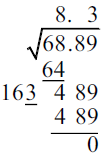
This method tells you directly when the answer is exact, by giving a remainder of 0.
This method is described here (in addition to the fuller explanation cited above):
Square Roots Without a Calculator (Doctor Robert, 1996) Longhand Square Roots (Doctor Rob, 1998)
Here is the corresponding way to find cube roots, and a detailed explanation of why it works:
Cube Root by Hand (Doctor Rob, 1998) Cube Root Calculation, Explained (Doctor Peterson, 2002)
A fourth method, described as Newton’s Method but really linear interpolation, is described here:
Manual Method for Finding Square Roots (Doctor Ethan, 1995)
Yet another ancient method is discussed here, showing how it is related to Newton’s method or Divide-and-average:
Bakhshali Formula (Doctor Peterson, 2002)
Comparison of all three methods
Which method is “best”? It depends on what you are looking for. Let’s explore the question by using each method for another, somewhat larger problem.
Example 6: Use each method to find the square root of 5678 to two decimal places.
(a) Guess-and-check:
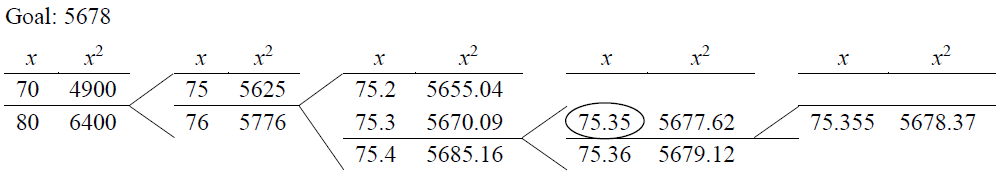
This took ten multiplications (because I mostly guessed well).
(b) Divide-and-average:
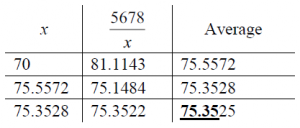
This took 6 divisions (including dividing by 2), most of them easy but two quite hard to do by hand.
(c) Longhand:
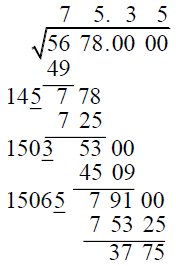
This took three multiplications and three fairly easy divisions, assuming I guessed everything right on the first try.
(d) Calculator: \(\sqrt{5678} = 75.3525049… \approx 75.35\)
Clearly they all give the same answer; see which one fits your style best. I find that, although we tend to push the last two, which seem more “mathematical”, the guess-and-check method may often involve less work for actual hand calculations. All are capable of identifying when an answer is exact.

Pingback: Too Much Guessing? – The Math Doctors
Thank you so much! Your examples and explanations on evaluating square roots by hand was something I used to help my 6th grader clearly understand.
What I liked: posting different methods with links to the original sources too, showing how these methods are useful later in calculus was very insightful, great use of examples, clear simple explanations, and clean minimalist web design.
Hats off to the great design and math team! This is the best math website I’ve ever used (as an engineer that is saying alot). Please dont ever take it down.
Pingback: Solving Equations with Newton’s Method – The Math Doctors
The TI-30XII calculator lets you iterate (ANS + A/ANS)/2 to get the square root of A with little wasted effort. Here A is the name of the variable into which the quantity called A in that formula is stored — two meanings to “A,” but should be clear. (It is assumed that the handling of STO, MEMVAR, and ANS are understood, and that it is straightforward to key in the expression above.) Even in 2025, this is a dandy non-graphing scientific calculator.
Example: Find √5678; guess 78
5678 STO ENTER (nowA = 5678 is in register A)
78 ENTER (now 78 is stored in ANS)
(ANS + A/ANS)/2 ENTER (result, 75.397 truncated)
ENTER (result, 75.35251832)
ENTER (result, 75.35350494)
ENTER (result, same as previous step)
Hi, P.W.
Of course, you can also use the square root button …
I have the same calculator sitting on my desk, so I could try it out immediately; you’ve used a feature I wouldn’t have thought of (and that didn’t work on another calculator I tried).
Where you say “A” in the third line, you really mean “RCL”, which recalls register A. I tried finding the square root of 10 using the horrible guess of 1, and it took only 7 iterations, which means only 3 more keystrokes! To show the work a little more literally than yours, it was
By default, MEMVAR functions to recall the variable A, and to put that variable name on the upper line of the display. MEMVAR -> recalls B, MEMVAR -> -> recalls C, etc., but MEMVAR lands you on A already selected.
A on the upper line serves exactly as it would in algebra when ENTER is pressed: its value is used in whatever expression is on the upper line. (So, for example, ABCDE ENTER yields the product of the corresponding five numbers.)
The expression (ANS + A/ANS)\2 can be input with the following keystrokes:
( 2nd ANS + MEMVAR / 2nd ANS)/2
I essentially do not use RCL at all; the variables do not clutter the display as messy numbers do (or overfill the display line), and remind me what variable I’m calling for.