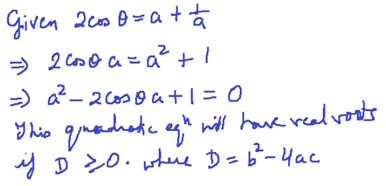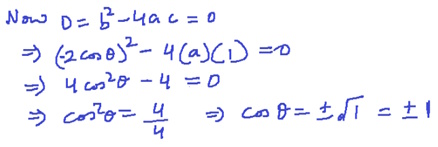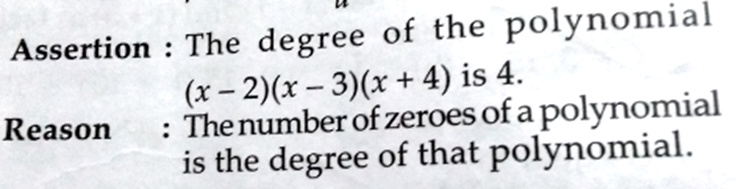Over the years, we have received several questions about problems that give an “assertion” and a “reason”, and ask you to decide whether each is true, and also whether the latter is “the correct explanation” (that is, a valid reason) that the former is true. These can involve subtle reasoning, and subtle errors. Since some involve the HCF/LCM ideas we looked at last time, this is a good time to examine these.
This genre of problem seems to be common in India (and not only for math topics); two of the three who have asked about them are from there.
Tricky trigonometry: unclear logic
We’ll start with this, from November 2021:
Hi,
I need to explain this to my daughter. However, I can’t give her a logical explanation. I looked it up online but couldn’t get anything useful.
I know the reason is correct. But I don’t know how to connect the assertion with the reason.
Pls help.
The “reason” is a (correct) statement of the range of the cosine; but what does the “assertion” even mean? Is it supposed to be true for all θ and all a, or something else? And is there any sense in which the domain of the cosine explains why it is true?
Harkirat’s work seems to be trying to determine for what values of θ the equation is true for some real values of a. He may be hoping to show, perhaps, that there will be at least one real root as long as \(-1\le\cos(\theta)\le1\), which is always true. And the latter statement is the “reason”, so, if true, this could be the connection. But the work doesn’t show that, and if taken further will show something quite different.
Doctor Rick answered:
Hello, Harkirat.
I would like to know if a preceding problem, or information given for a set of problems including this one, gives any further information that would put the “assertion” into context.
As it stands, with nothing said about what θ and a are, the “assertion” seems incomplete; I would expect it to include some logical quantifiers (such as “there exists”, “for all”, …). Here are some possibilities:
For any a > 0, a ≠ 1, there exists some θ such that 2 cos θ = a + 1/a. [1]
For any θ, there exists some a (a > 0, a ≠ 1) such that 2 cos θ = a + 1/a. [2]
There exist some θ and some a (a > 0, a ≠ 1) such that 2 cos θ = a + 1/a. [3]
For any θ and any a (a > 0, a ≠ 1), it is true that 2 cos θ = a + 1/a. [4]
The assertion [4] (which is how I interpret the assertion in the absence of further information) is clearly false, and only option (d) says this. Furthermore, you have noted that the “reason” is true, and (d) says nothing about whether the “reason” explains the assertion, only whether it is true.
But to me, [4] is too obviously false, and I’d want the problem to be more interesting, so I would consider the other versions above.
A bare equation involving unspecified variables is not properly called an assertion (or statement) at all; we can’t say whether it is true or false, unless we add, say, “when \(a=3\)” or “for all a” or “for some a“. This is what “quantifier” means.
It appears that Harkirat is interpreting the assertion as [2]: that there is some a that works, regardless of the value of θ.
What you have done shows that the equation is true for a single value of a if cos θ = ±1, because you found the values of θ for which D = 0, not D ≥ 0. That in itself is not significant as far as I can tell. However, if you continue on to determine for what values of θ the equation has any real solutions (which are the only solutions considered at this level of trigonometry), you will find something interesting. A related approach would be to find the range of the function f(a) = a + 1/a.
As I’ve said once before, I hope that when you say you want to explain this to your daughter, you mean that you will guide her in doing as much of the solving as possible herself. But first we need to be sure we understand what the problem is saying.
If the range of \(f(a)\) (for positive a) includes the entire range of \(2\cos(\theta)\), then there will be an a for every θ.
Harkirat replied:
Hi Rick,
I’ve sent the picture of the Assertion/Reason question as it was given in the book. Due to the COVID pandemic, this is the first time students are going to have an exam comprising only of MCQs. My daughter bought some books to practice and this question is from one of the books. I feel these questions are beyond what they have been taught in the syllabus. I’m trying to help her myself as I can’t afford private tutors. I studied all this 40 years ago and now find it difficult to tackle such questions. What to do?
But isn’t the “REASON” true by itself? Doesn’t the value of cos theta lie between -1 and 1?
Anyway, thanks for your help.
The problem is difficult even for us! It is undoubtedly not a good test of knowledge of the syllabus.
Doctor Rick responded:
I would need to see more than this one question in order to be sure that there is no contextual information that could help. However, I doubt that there is any; I believe this is simply a poorly written question. Unless this is a problem from an official exam of a prior year, I would not worry about it, but go on to other problems.
Yes, the “reason” is true as you say. I noted that the likely intended answer,
(d) Assertion (A) is false but reason (R) is true
does not claim, as (a) does, that “reason (R) is the correct explanation of assertion (A)”, but only that it is true. Of course, you can’t have a correct explanation of a false statement; but they could have asked whether (R) is “the explanation” for the falsehood of (A), and then we would have a more difficult task. In my mind, (R) is part of the reason why (A) is false.
We’ll be seeing other problems of this sort where there is some ambiguity in the very idea of R being “the correct explanation” of A, as well as in what it means for A to be true. It is not hard to make poorly written questions of this type!
Did you finish working out which of my four statements is correct? You were on the right track; you can show that
D ≥ 0 if and only if cos θ ≥ 1 or cos θ ≤ –1
Therefore the equation
2 cos θ = a + 1/a
can only be true if cos θ = ±1, that is, θ = πk for some integer k. But further work will show that if cos θ = ±1, then a must be ±1. (These are the solutions to the equations a2 + 2a + 1 = 0 and a2 – 2a + 1 = 0.) And the assertion stated that a > 0 and a ≠ 1; therefore we see that the assertion is not true for any of the allowed values of a. Therefore all four of my statements are false.
So, though it takes some work to see it, no matter how we interpret A, it is false; and R is part of the explanation for that. Fortunately, only answer (d) fits.
Here are the graphs of \(f(a)=a+\frac{1}{a}\) in red, and of \(g(\theta)=2\cos(\theta)\) in blue:
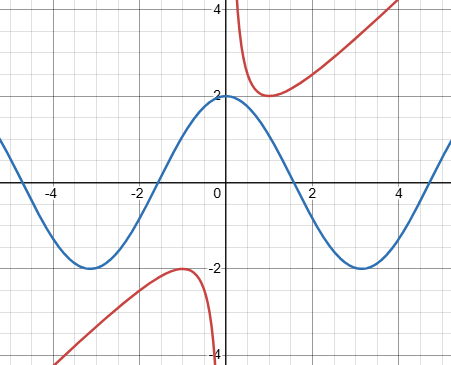
We can see that the only way \(f(a)\) and \(g(\theta)\) can be equal is if both are equal to 2 or -2, so that a has to be 1 or -1.
Polynomial zeros and degrees: subtle logic
Next, here is a question from Akshita in Jume 2023:
We want to see your own thinking, or at least specific questions about it, when you ask about a problem; we’ll get there! While we wait, what do you think about this one?
Doctor Rick answered, checking on the instructions, which were omitted:
Hi, Akshita.
You did not say what the problem asks you to do. My guess is that you are supposed to do two things: (1) say whether the assertion is true, and (2) say whether the reason is valid. We might break down the second of these into two parts: (2a) Is the “reason” a true statement? (2b) Is the “reason” sufficient to prove the “assertion”?
I shouldn’t have to guess. Please tell us the complete problem. In addition, we need to know your own thoughts about the problem. What do you think is the answer? What are you unsure of, that led you to ask us about it?
As often happens, there are several issues that he might have seen, and we don’t want to answer the wrong one.
Akshita showed the instructions (which turn out to be identical to Harkirat’s) and his thoughts:
Upon multiplication I get the degree of polynomial as 3. In essence meaning the assertion is false. Talking about the reason, the max no. of zeroes of polynomial = degree of polynomial. We can’t state that the no. of zeroes of polynomial is its degree.
I come across the following conclusion, assertion and reason both are false but that’s not given in the option.
In the book the answer happens to be option (d).
This led me to post the question on your site for help
I’m curious why the possibility that “both statements are false” is not included as a fifth choice! But this is the standard wording for such problems.
Doctor Rick could now say more:
Thank you, I needed to know all of this in order to help you.
I agree with you! I too would say that the Assertion is false (because the degree of the given polynomial is 3) and that the Reason is invalid (because the number of zeroes of a polynomial is at most the degree of the polynomial).
However, there is a way to interpret the Reason such that it is valid. First, we need to read “zeroes” as all zeroes of the polynomial over the complex numbers — not just real zeroes. This is true; we really shouldn’t think that “zeroes” means only real zeroes. In addition, however, we need to read the “number” of zeroes as including multiplicities — that is, a zero of multiplicity n is counted n times. Properly speaking, it’s the number of distinct real zeroes that is less than or equal to the degree.
If the book defines the number of zeroes of a polynomial in exactly this way, then its answer is correct. Otherwise, I would say the problem is not entirely clear, as the Reason can reasonably be interpreted in more than one way.
There was no further discussion. But if we take the numbers of zeroes as suggested here (the number of complex zeroes counting multiplicity), then the Reason (number of zeroes is the degree) is true, and this implies that the given polynomial, with 3 zeroes, has degree 3, so that the Assertion is false. Thus, answer (d) does make some sense.
HCF and LCM, and vacuous logic
We received this question from a teacher last December, just quoting the problem (completely, this time!):
Assertion (A): The HCF of two numbers is 9 and their LCM is 2016. If the one number is 54, then the other number is 336.
Reason (R): The relationship between two numbers and their HCF and LCM is:
a × b = HCF(a, b) × LCM (a, b)
Choose the correct option from below
(A) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
(B) Both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A).
(C) Assertion (A) is true but Reason (R) is false.
(D) Assertion (A) is false but Reason (R) is true.
Checking the assertion
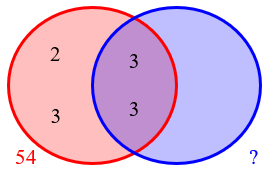
Before looking at the question as a whole, let’s think about the assertion alone, which is similar to our first problem from last time. First, using the (correct) identity stated as R, we know that given \(HCF=9\), \(LCM=2016\), and \(A=54\), we can conclude that $$B=\frac{HCF\cdot LCM}{A}=\frac{9\cdot2016}{54}=336$$ So the assertion, at first glance, appears to be true.
But, like last time, we should check that answer! Is 9 the HCF of \(54=2\cdot3^3\) and \(336=2^4\cdot3\cdot7\)? No, 9 isn’t a factor of 336 at all! And is 2016 their LCM? No, that’s \(2^4\cdot3^3\cdot7=3024\).
If we try to fill in our diagram from last time, after putting in the factors of the HCF and of 54, we look at the factors of 336, \(3\cdot2\cdot2\cdot2\cdot2\cdot7\), and the two 3’s can’t be in that circle!
If, like last time, we ignore what we are told about the first number and just try to find any possible pairs of numbers, we see that, after filling in the HCF, we are left with these factors of the LCM to distribute in the empty spaces:
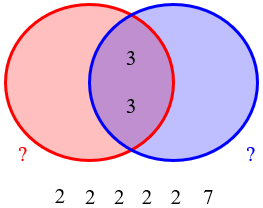
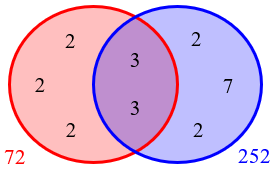
There are many choices, but since there are no 3’s left to distribute, one of them will not be \(A=54\)! We could, for example, put \(2\cdot2\cdot2\) on the left, and the remaining \(2\cdot2\cdot7\) on the right:
What’s the logic?
I didn’t want to say too much without knowing what Atif had in mind, so I just asked the usual question:
Hi, Atif.
Please tell us your thoughts about the problem. I can see something you might be unsure of, but I want to be sure I am dealing with the right issue.
Atif replied:
I feel option a is the correct answer, but some of my students say option d is the correct answer. So I need your help to convince me which option is correct.
So Atif thinks assertion A is true, and reason R is the correct explanation, while some students think assertion A is false. From what I said above, which is correct?
I wanted just a little more information, due to the extreme subtlety of the issue:
Now please tell me the reasons given for each of the two answers. That is, how do you and the students justify each answer?
I expect that the difference between the two will depend on a subtlety we’ll need to discuss, and your class needs to do so as well! (I can support either answer, though you are technically correct.)
A day later, with no response, I said what was on my mind:
The problem says:
Assertion (A): The HCF of two numbers is 9 and their LCM is 2016. If the one number is 54, then the other number is 336.
Reason (R): The relationship between two numbers and their HCF and LCM is:
a x b = HCF (a, b) × LCM (a, b)
The difficulty is that 54 can’t be one of the two numbers, because the HCF of 54 and 336 is not 9 but 6: 54 = 2*3^3, and 336 = 2^4*3*7, so that 54 = 6*9 and 336 = 6*56.
So, is the statement “If the one number is 54, then the other number is 336″ true or false? Technically, it is vacuously true, as the condition is false. This is discussed in Why, in Logic, Does “False” Imply Anything?. So (a) is correct, but students have good reason to think otherwise.
This might be more understandable if we take it as “If the one number were 54, then the other number would be 336.”
Is that your thinking?
We never heard more; when I showed the problem to a colleague, she saw the difficulty quickly, and was amused as I was.
My impression is that assertion/reason questions, which I see used in many fields, are not primarily intended to test logic, but the content of the assertions. So the difficulty in such a problem ought not to be tricky logic!
Most likely the author simply didn’t check the assertion, and so didn’t even notice the issue; the result is an example of the sort of problem that (accidentally, we hope) is harder for truly good thinkers than for those who don’t pay close attention.
I found several sites giving the answer as (a), and none mentioned the vacuous truth of the assertion, or even did the check.