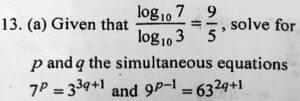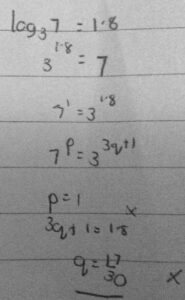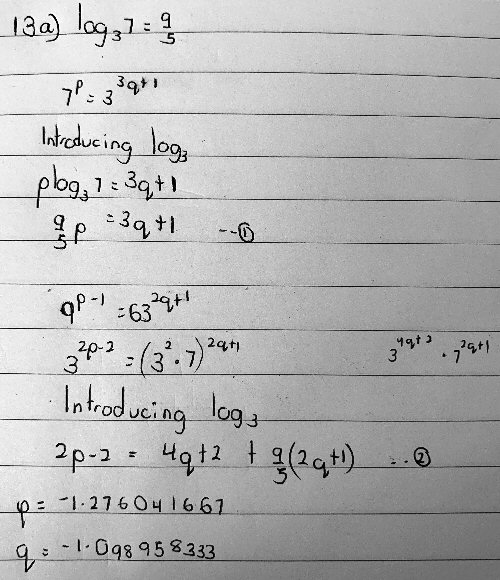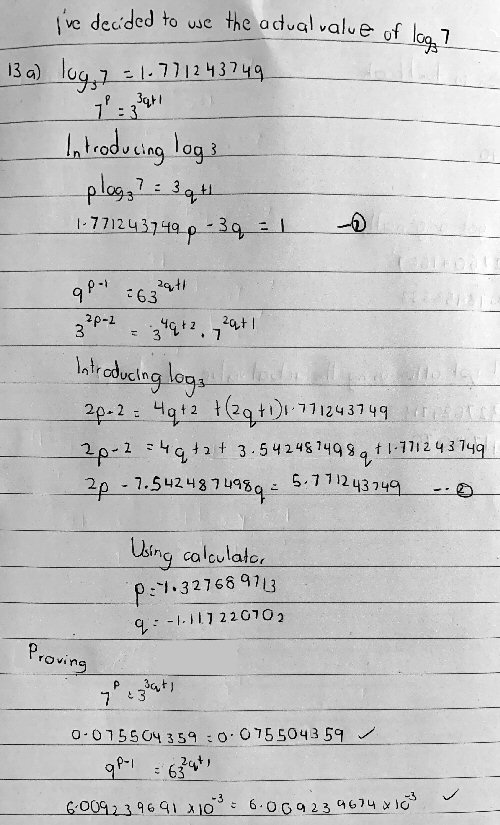What do you do when you are given a problem that starts with a “lie” and ends with a wrong answer? We’ll go in several directions with this problem, a system of two exponential equations in two variables.
The problem, and a failed attempt
It came from Eli in May 2022:
Hello! This is my first time using Dr. Math. I worked out a question on finding unknowns in indices but my answers were not even close to the final answer I was supposed to get. I’m assuming it’s a misconception I have to unlearn concerning my algebra. Could you please help me find it?
Doctor Fenton answered:
Hi,
This is a strange question, since its premise is false. The quotient
(log10(7))/(log10(3))
is NOT 9/5.
As you calculated, 9/5 = 1.8, but (log10(7))/(log10(3)) = 1.771243749… , so 1.8 is only a rough approximation, not an exact value.
Mathematicians are accustomed to using exact values, so starting with a technically false statement feels wrong. We’ll see that the “approximate lie” we’re starting with is not entirely a bad idea, but it can lead to confusion!
You correctly used the change of base formula to write (log10(7))/(log10(3)) = log3(7), so log3(7) would be 9/5, if the “given” were true. However, you have only used one of the equations, while the problem asked you to find the solution of a set of simultaneous equations. I’m not sure what they expect you to do.
One possibility is to “pretend” that indeed log3(7) = 1.8, find the two equations for p and q, and solve for p and q.
(Alternatively, you could think that instead of 7, there is a number x such that log3(x) = 9/5, and such that xp = 3q+1, and 9p-1=(9x)2q+1. Now solve for p and q.)
Can you rewrite the two exponential equations as linear equations in p and q, using one of the modified assumptions? If so, can you solve the equations for p and q?
Yes, we will be “pretending”, and thus finding an approximate answer. Eventually, we’ll transform the problem into a useful technique for finding accurate answers.
We’ll be looking back at Eli’s work later.
A better try … in fact, it’s correct!
He answered:
Hello, once again.
I expressed the two exponential equations linearly but somehow I am still getting different answers from what they expect. Maybe it’s an algebraic error on my side or maybe they were wrong but I will need your answers to confirm.
We’ll see that, in fact, they are wrong …
Let’s carry out the work to solve the system of linear equations.
He took logs, $$\log_3\left(7^p\right)=\log_3\left(3^{3q+1}\right)\\\log_3\left(9^{p-1}\right)=\log_3\left(63^{2q+1}\right),$$ expanded to make linear equations,
$$p\log_3\left(7\right)=(3q+1)\log_3\left(3\right)\\(p-1)\log_3\left(9\right)=(2q+1)\log_3\left(63\right),$$ and then inserted the assumption, knowing that \(\log_3(63)=log_3(3^2\cdot7)=2+log_3(7)\):
$$\frac{9}{5}p=3q+1\\2p-2=4q+2+\frac{9}{5}(2q+1)$$
This simplifies to $$\frac{9}{5}p-3q=1\\2p-\left(4+\frac{18}{5}\right)q=4+\frac{9}{5}$$
Multiplying both equations by 5 to clear fractions, we get $$9p-15q=5\\10p-38q=29$$
Adding 38 times the first equation and -15 times the second to eliminate q, we add them and get $$(9\cdot38-10\cdot15)p=(5\cdot38-29\cdot15)\\\\192p=-245\\\\p=\frac{-245}{192}=-1.2760416…$$ Adding -10 times the first equation and 9 times the second to eliminate p, we get $$(15\cdot10-38\cdot9)p=(-5\cdot10+29\cdot9)\\-192p=211\\p=\frac{211}{-192}=-1.0989583…$$
So it turns out that he solved the system correctly, but his value for p disagrees with the book. Is there an error in the setup, or is the book wrong?
Doctor Rick joined in:
You’re doing a lot better this time; your linear equations in p and q look correct to me. The error must be in the details of your solution of that system, which you did not show.
You could test your solution by plugging the numbers into the two original equations (using a calculator). I find that it does not satisfy the first of the equations, but it comes pretty close to satisfying the second equation. There is probably a reason for this, that might help us track down your error.
Of course, since we’re using an inexact logarithm, we don’t expect an exact match; but let’s do the check. Setting \(p=-1.276\) and \(q=-1.099\), we get:
$$7^p=7^{-1.276}=0.08349\\3^{3q+1}=3^{3(-1.099)+1}=3^{-2.297}=0.080177$$ which are close, and
$$9^{p-1}=9^{-1.276-1}=9^{-2.276}=0.006732\\63^{2q+1}=63^{2(-1.099)+1}=63^{-1.198}=0.006989$$ which are also close. I’m not sure what difference Doctor Rick saw; possibly the expectation that the answer would be wrong led him to see a small difference as more significant than it is, or perhaps to not catch an error of his own.
My take on the “false premise” that Doctor Fenton pointed out is that it’s a little like when students are told to solve some problem involving circles, with the instruction to “use 22/7 as the value of pi“. That, too, is only an approximation. In your problem, the quantity you’re given also provides a clue to a solution method (which you’ve figured out now). However, the trouble with using an approximate value is that when you do as I suggested and test your solution by plugging in, you won’t get an exact match. A couple of digits matching is all you can expect.
I often help students who have been told to use 3.14 for π, presumably either because they are not expected to use a calculator, or because they’ve been asked to memorize that value, or just out of tradition. Here, I think the purpose is a little different, since the students probably are not expected to solve the problem entirely by hand. I suspect that the intent is similar to problems I’ve seen that might say, “Using a certain base, \(\log(3)=0.68\) and \(\log(7)=1.21\). Find \(\log(63)\),” where the point is to find a way to use the (approximate) information given. But it does also provide a hint that might guide a student through what would otherwise be a complicated problem. We’ll be taking that idea a little further.
But the fact that we can’t check our answer with certainty makes it an unsatisfying problem.
What if we don’t use the approximation?
Eli responded with a different sort of check:
Hey!
I have gone over my method multiple times and get the same answer every time as previously indicated.
The funny thing is that one of my values doesn’t match the answers given. Which I find almost impossible, for how can I solve simultaneous equations and only get one of them right? So I decided to test the values of p and q I attained and as you said, one of the statements is pretty close to being correct while the other has a very high error. This frustrated me so I decided to prove the statements with the answers given to me that were supposed to be correct. That didn’t work out very well because the errors were in hundreds. So I concluded they were wrong. I finally decided to use the real value of the logarithm given in the question instead of the value given and after proving, I managed to get both sides of the equations equal.
Now we finally know what the book said, and can be sure that their error is the cause of the struggle! Their q agrees with Eli’s, to four decimal places; but their p is entirely different.
If we do the same check as before, for \(p=2.9\) and \(q=-1.099\), we find, for the first equation, that $$7^p=7^{2.9}=282.3\\3^{3q+1}=3^{3(-1.099)+1}=3^{-2.297}=0.080177$$ which are hardly even in the same universe.
Clearly, though, the work is easier using the approximation, which keeps the numbers small! One way to avoid the long decimals is to use a named parameter instead of the actual value, and only put in the value at the end. Let’s try that:
The equations are $$7^p=3^{3q+1}\\9^{p-1}=63^{2q+1}$$
Following the hint without the numerical value, we can just express everything in terms of a constant \(\log_3(7) = c\):
$$\log_3\left(7^p\right)=\log_3\left(3^{3q+1}\right)\\\log_3\left(9^{p-1}\right)=\log_3\left(63^{2q+1}\right)$$
Simplifying,
$$p\log_3\left(7\right)=(3q+1)\log_3\left(3\right)\\(p-1)\log_3\left(9\right)=(2q+1)\log_3\left(63\right)$$
Since \(\log_3\left(9\right)=\log_3\left(3^2\right)=2\) and \(\log_3\left(63\right)=\log_3\left(3^2\cdot7\right)=2+\log_3\left(7\right)=2+c\), this becomes
$$cp=3q+1\\2(p-1)=(2+c)(2q+1)$$
Rearranging,
$$cp-3q=1\\2p-(2c+4)q=c+4$$
Eliminating q,
$$c(2c+4)p-3(2c+4)q=2c+4\\-6p+3(2c+4)q=-3(c+4)$$
$$c(2c+4)p-6p=2c+4-3(c+4)\\(2c^2+4c-6)p=-c-8\\p=-\frac{c+8}{2c^2+4c-6}=-\frac{c+8}{2(c+3)(c-1)}$$
This is an exact answer!
Similarly, eliminating p,
$$2cp-6q=2\\-2cp+c(2c+4)q=-c(c+4)$$
$$(2c^2+4c-6)q=-(c^2+4c-2)\\q=-\frac{c^2+4c-2}{2c^2+4c-6}=-\frac{(c+2)^2-6}{2(c+3)(c-1)}$$
Using our approximate value \(c\approx1.8\), this becomes \(p=-\frac{9.8}{2(4.8)(0.8)}=-1.276\) and \(q=-\frac{3.8^2-6}{2(4.8)(0.8)}=-1.099\), just as he got.
Using the actual value of c, we get, once again, \(p=-1.32769\) and \(q=-1.11722\).
Doctor Fenton answered again:
I get the same values for p and q that you get, both for the case when log37 = 9/5, and when log37 is given its correct value. Whoever solved the problem obviously didn’t check their answer, since it is clearly wrong. If p=2.9, then 7p is nearly 73, which is over 300, while the right side must be less than 3, since q<0 so that 3q-1 < 1.
So, where did their answer of 2.9 come from? Looking at my own work,
$$9p-15q=5\\10p-38q=29$$
I notice that \(p=2.9\) if \(q=0\) in the second equation. Might they have lost the q term there?
What was wrong with the first attempt?
Eli was still curious:
Thank you for all the help but there’s still one thing bugging me. Why didn’t my original method work? The one where I used only one of the equations
I responded:
Here is what you wrote:
71 = 31.8
7p = 33q+1
p = 1
3q + 1 = 1.8
The trouble is that you just assumed that the two exponents are 1 and 1.8 respectively; or, equivalently, you just assumed that p is 1, and found what q would be in that case. But the other equation doesn’t permit that to be true.
So what he did was just to compare the given approximate fact (converted to exponential form) with the first equation and suppose that the exponents in both equations are the same, which is one way to make the equation true. This is only one possibility to satisfy the first equation.
Looking back at Eli’s original work, I wee that there is also an arithmetic error; he solved \(3q+1=1.8\) as if it were \(3q+0.1=1.8\), to get \(q=\frac{17}{30}\) rather than \(q=\frac{8}{30}\).
All you can really deduce from this first equation is that p and 3q+1 are proportional to 1 and 1.8, not that p and q have those particular values. One way to see this is to replace 7 with 31.8 in the first equation, which becomes (31.8)p = 33q+1, and therefore 1.8p = 3q+1. This is essentially what you did in your corrected work.
(There are several ways to work this problem; I myself took the base-10 log of each equation.)
Doctor Fenton concurred:
The equation 7p = 33q+1 is equivalent (after taking the logarithm of both sides to the base 3) to the equation
(log3 7)p = (3q+1) , or (log3 7)p – 3q = 1 .
The last equation is a line (in the p-q plane), so when p = 1, 3q = log3 7 – 1, or q = (log3 7 – 1)/3. Assuming log3 7 = 9/5, q = 4/15. But (1, 4/15) is just one point on this line. The single equation cannot determine the values of both variables. For any value of p, there is a corresponding value of q which will satisfy the equation. You can’t just assume that p = 1. p can have any value: once you have chosen a value for p, there will be a corresponding value for q making the equation true.
The second equation can also be turned into the equation of a line, which has a different slope from the line corresponding to the first equation. These two lines then must cross, and finding the solution of the simultaneous equations locates the crossing point. That is what the problem is looking for, and why you must consider both equations.
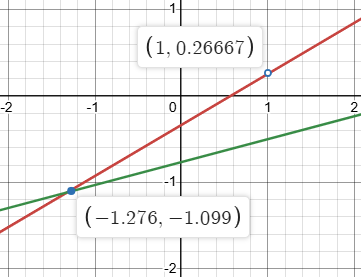
Here is a graph of both equations (first in red, second in green), showing the correct answer as a blue dot, and Eli’s original answer (with my correction, \(q=\frac{8}{30}\)) as an open dot, showing that it is only (approximately) on the first line, not the second:
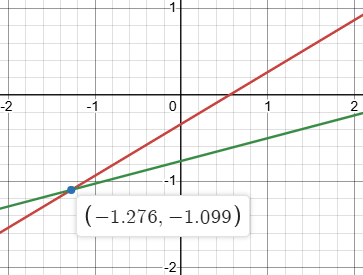
If we replace 7 in both equations with \(3^{1.8}\), we can see that this solution actually satisfies the resulting equations:
Here is the actual solution, without using the approximation, showing it lies on both of the actual equations as given:
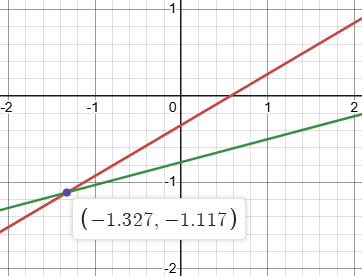
The differences in the lines and the solutions are hardly noticeable, but would matter if precision were important.
What if we didn’t have the “hint”?
I’d like to try solving the problem without any approximations or even hints. We have
$$7^p=3^{3q+1}\\9^{p-1}=63^{2q+1}$$
What might we do? My first thought might be to look at the bases and see that they are all products of 3 and 7 only, with 3 perhaps a little more common; so I might start by factoring the bases and writing them all in terms of 3 and 7:
$$7^p=3^{3q+1}\\(3^2)^{p-1}=(3^2\cdot7)^{2q+1}$$
$$7^p=3^{3q+1}\\3^{2p-2}=3^{4q+2}7^{2q+1}$$
$$7^p=3\cdot3^{3q}\\\frac{1}{9}3^{2p}=9\cdot3^{4q}7\cdot7^{2q}$$
Now, I’m inclined to take base-3 logs everywhere:
$$p\log_3(7)=1+3q\\-2+2p=2+4q+\log_3(7)+2q\log_3(7)$$
To keep things simple, I might give a short name to \(\log_3(7)\), and just call it c. (This is the hint, rediscovered!) Using that, and rewriting, I get
$$cp-3q=1\\2p-(2c+4)q=c+4$$
And we’re on the way to either the exact solution,
$$p=-\frac{\log_3(7)+8}{2(\log_3(7)+3)(\log_3(7)-1)}\\q=-\frac{(\log_3(7)+2)^2-6}{2(\log_3(7)+3)(\log_3(7)-1)},$$
from my work earlier, or the one using any approximation we want, including
$$p=-\frac{1.8+8}{2(1.8+3)(1.8-1)}\\q=-\frac{(1.8+2)^2-6}{2(1.8+3)(1.8-1)}$$