(An archive question of the week)
In preparing the last couple posts, on recurrence relations, I ran across an answer to a much harder question, that illustrates what it can take to solve one that doesn’t fit the convenient forms. It’s linear, but the coefficients are not constant as they have been in all our other examples. This is where creativity becomes your most important asset.
A linear recurrence with non-constant coefficients
Here is the question, from 2005:
Second Order Recurrence with Non-Constant Coefficients Hello. I ran into this second order recurrence relation with non-constant coefficients and I was wondering what would be the best way to get a closed form solution in terms of the initial values u(0) and u(1). u(n+2) = 2*(2*n+3)^2 * u(n+1) - 4*(n+1)^2*(2*n+1)*(2*n+3)*u(n) What I find most difficult is the presence of non-constant coefficients in the recurrence relation. Had it been involving only constant coefficients things would have been much easier to solve. I tried noticing a certain repeating pattern but that is very hard to detect. I was thinking of finding an equivalent second order differential equation whose series expansion would yield the required recurrence relation but that also didn't lead to anywhere interesting. I am interested in getting a closed form solution for this recurrence. Any help would be highly appreciated. Thanks!
Let’s take a moment to examine the sequence, and produce a specific example we can check against in the end. The recurrence is $$u_{n+2}=2(2n+3)^2u_{n+1}-4(n+1)^2(2n+1)(2n+3)u_n$$ Alternatively, to make it look more like most of our examples where the left-hand side is the nth term, we could replace \(n+2\) with \(n\) (that is, replace \(n\) with \(n-2\)) everywhere and obtain $$u_{n}=2(2n-1)^2u_{n-1}-4(n-1)^2(2n-3)(2n-1)u_{n-2}$$
I arbitrarily chose \(u_0=1,u_1=3\). Here is the sequence:
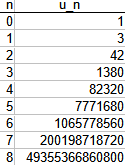
For example, $$u_2=2(2(2)-1)^2u_1-4(2-1)^2(2(2)-3)(2(2)-1)u_0\\=18u_1-12u_0=18(3)-12(1)=42$$
Doctor Vogler answered:
Hi Bassam, Thanks for writing to Dr. Math. Unfortunately, recurrence relations are very much like sums in that MOST of them cannot be solved in closed form. That is, most of them can't be solved with a nice, neat, simple formula. But some of them can. For both sums and recurrences, there are those that have nice forms (like geometric sums and linear recurrences) which can be solved by very straight-forward techniques. And then there are a few special ones (like the sum of 1/n^2, or your recurrence) that can be solved with enough effort.
This is true not only of summing series (for example, there is no closed form for \(\displaystyle\sum_{i=1}^n\frac{1}{n}\), which we’ll run across later) but also of differential equations and even integrals. In each case, there are standard methods for special cases, while others need great creativity, or simply can’t be solved (exactly) at all.
Experimenting with factors
Fortunately for you, yours is solvable. But I didn't know this at first. In any case, you might as well try. How do you try to solve a recurrence relation? Well, as with sums, there are various techniques, and not all of them work all of the time. But let's see what we can do. So the first thing I noticed was that both terms in your recurrence are divisible by 2n+3. So let's suppose that u(0) and u(1) are integers. Then all u(n)'s will also be integers. And u(n+2) will always be divisible by 2n+3. That means (replacing n by n-2) that u(n) will always be divisible by 2n-1.
This last statement is obvious if we rewrite our recurrence as $$u_{n}=(2n-1)\left(2(2n-1)u_{n-1}-4(n-1)^2(2n-3)u_{n-2}\right)$$
It is not necessary that the first two terms be integers; but seeing what happens in that case can suggest facts that will apply more generally. Restricting a problem can help solve the full problem.
Great! We're getting somewhere! Now 2n+1 divides the second term, but 2n+1 divides u(n+1), which means it also divides the first term! So 2n+1 also divides u(n+2), and therefore 2n-3 divides u(n). You can continue in this way and show that 2n-5 divides u(n), and 2n-7, and so on.
That is, sticking with the original form of the recursion, $$u_{n+2}=2(2n+3)^2u_{n+1}-4(n+1)^2(2n+1)(2n+3)u_n$$ the second term contains a factor \(2n+1\), and the first term contains \(u_{n+1}\), which we now know is divisible by \(2(n+1)-1 = 2n+1\). The whole expression for \(u_{n+2}\) is therefore a multiple of \(2n+1\).
Again replacing \(n\) with \(n-2\), this tells us that \(u_n\) is therefore a multiple of \(2(n-2)+1=2n-3\).
Repeating, as he suggested (for the moment I’ll work with the \(u_n\) form of the equation), in $$u_{n}=(2n-1)\left(2(2n-1)u_{n-1}-4(n-1)^2(2n-3)u_{n-2}\right)$$ looking only inside the outer parentheses, the second term contains \(u_{n-2}\) which is a multiple of \(2(n-2)-1=2n-5\), and the first term contains \(u_{n-1}\) which is a multiple of \(2(n-1)-3=2n-5\), so the entire thing is a multiple of \(2n-5\). This can be repeated all the way down … to negative infinity? No, only back to the first term the recurrence applies to.
We now have \(u_n\) being a multiple of \((2n-1)(2n-3)(2n-5)\cdots\), so that \(u_{n+2}\) is a multiple of \((2n+3)(2n+1)(2n-1)\cdots\); this is called the double factorial (though if there weren’t a name or symbol for it already, we would just create a name):
So then we recall a definition n!! = n*(n-2)*(n-4)*(n-6)*...*u where u is either 1 or 2, according to whether n is odd or even. Then we divide the whole equation by (2n+3)!! and set a(n) = u(n)/(2n-1)!!. Then the recurrence becomes a(n+2) = 2*(2n+3)*a(n+1) - 4*(n+1)^2*a(n).
That is, we have gone from $$u_{n+2}=2(2n+3)^2u_{n+1}-4(n+1)^2(2n+1)(2n+3)u_n$$ to $$a_{n+2}=\frac{u_{n+2}}{(2n+3)!!}=\frac{2(2n+3)^2u_{n+1}}{(2n+3)!!}-\frac{4(n+1)^2(2n+1)(2n+3)u_n}{(2n+3)!!}\\=2(2n+3)\frac{(2n+3)u_{n+1}}{(2n+3)(2n+1)!!}-4(n+1)^2\frac{(2n+1)(2n+3)u_n}{(2n+3)(2n+1)(2n-1)!!}\\=2(2n+3)\frac{u_{n+1}}{(2n+1)!!}-4(n+1)^2\frac{u_n}{(2n-1)!!}\\=2(2n+3)a_{n+1}-4(n+1)^2a_n$$
(He accidentally omitted the 2 and 4; I corrected that above after wasting time using his recurrence in a spreadsheet to check this!)
Looking at our specific example, we see that \(u_3=1380\), and \((2(3)-1)!!=5!!=(5)(3)(1)=15\), so that \(a_3=\frac{u_3}{15}=\frac{1380}{15}=92\).
A leap of faith
This transformed our recurrence on \(u_n\) to a simpler recurrence on \(a_n\):
Even better! Now we have reduced the degree of the coefficients by 1 and 2, respectively. Can we do more? Well, we can try to show that these a(n)'s are divisible by some similar factorial, but it's just not always true. Nevertheless, they do grow about as fast as a factorial. We might try dividing by a polynomial in n, or something like that, but it won't reduce the degree of those coefficients; we need factorials for that.
It appears that nothing quite works (and I imagine a lot of trying is hidden behind these words!). But we can back up, take a running leap, and see what happens:
So what happens if we take a leap of faith? We really want to reduce the degree of those coefficients, so let's divide by a full factorial: Let's divide the original equation by (2n+3)! and set
b(n) = u(n)/(2n-1)!.
Then the recurrence becomes
2n+3 n+1
b(n+2) = 2(----)*b(n+1) - (---)*b(n).
2n+2 n
He has gone back to the original equation, abandoning \(a_n\), and instead of dividing by the double factorial, divided by the factorial itself (which in effect means dividing \(a_n\) again by all the factors the double factorial missed).
Here’s the work he skipped:
$$b_{n+2}=\frac{u_{n+2}}{(2n+3)!}=\frac{2(2n+3)^2u_{n+1}}{(2n+3)!}-\frac{4(n+1)^2(2n+1)(2n+3)u_n}{(2n+3)!}\\=\frac{2(2n+3)^2u_{n+1}}{(2n+3)(2n+2)(2n+1)!}-\frac{4(n+1)^2(2n+1)(2n+3)u_n}{(2n+3)(2n+2)(2n+1)(2n)(2n-1)!}\\=2\frac{2n+3}{2n+2}\frac{u_{n+1}}{(2n+1)!}-\frac{4(n+1)^2}{(2n+2)(2n)}\frac{u_n}{(2n-1)!}\\=2\frac{2n+3}{2n+2}b_{n+1}-\frac{n+1}{n}b_n$$
Now we have a recurrence in \(b_n\) whose coefficients are not quite constants, but very nearly so.
So the cost of our leap of faith is fractions. But you might notice that those fractions are *nearly* one, and so our recurrence is *almost* b(n+2) = 2b(n+1) - b(n), which is an easy recurrence to solve. In fact, its solutions are b(n) = C*n + D.
So we’ve almost turned it into a linear recurrence with constant coefficients, which we know how to handle. (The solution shown here comes from solving the characteristic equation \(x^2-2x+1=0\), whose only solution is \(x=1\), making the general solution \((Cn+D)(1)^n\).)
Turning “almost” into “just right”
We know how to handle recurrences that are “almost” what we want except for a non-homogeneous term; what if we do something like what we do there?
Unfortunately, that *almost* means that this is not quite correct. But what happens if we subtract off the nice part and put that on the left side of the equation?
b(n+1) b(n)
b(n+2) - 2b(n+1) + b(n) = ------ - ----.
n+1 n
Well, that's not too bad. It has some nice symmetry going on, especially with the denominators on the right matching the indices. For example, we might suspect that we could get one solution by supposing that both sides of the equation are zero. On the right, that would mean b(n)/n is constant, and that also solves the left side too!
This is an example of hopeful thinking, which sometimes works in math, at least as a starting point: This would be easy if the two quantities that are equal turned out to be equal to zero, so let’s just see if that happens to work! And it does: The solution to \(b_{n+2}-2b_{n+1}+b_n=0\) has the form \(b_n=Cn+D\), while the solution to \(\frac{b_{n+1}}{n+1}-\frac{b_{n}}{n}=0\) is \(b_n=Cn\), which is a particular case of the former.
But we can do better! In fact, the left side is a difference of differences
[b(n+2) - b(n+1)] - [b(n+1) - b(n)],
and the right side is also a difference. So let's pair up the differences!
b(n+1) b(n)
b(n+2) - b(n+1) - ------ = b(n+1) - b(n) - ----.
n+1 n
That means that the sequence
b(n)
c(n) = b(n+1) - b(n) - ----
n
is constant!
Recognizing a pattern in the equation allowed us to find an invariant, which is really a coup. The result is a first-order recurrence in disguise:
So let's write
b(n)
b(n+1) - b(n) - ---- = K
n
and then solve
n+1
b(n+1) = K + (---)*b(n).
n
If we take K = 0, then that is the solution I mentioned previously. Otherwise, we start substituting
n
b(n) = K + (---)*b(n-1).
n-1
n n-1
= K + (---)*[K + ---*b(n-2)]
n-1 n-2
n n n n
= K + ---*K + ---*K + ... + -*K + -*b(1).
n-1 n-2 2 1
This amounts to the iteration method for seeing a pattern in a first-order recurrence. As in previous posts we have seen an arithmetic series and a geometric series arise by similar iteration (and could use their formulas), here we end up with a harmonic series (for which, unfortunately, there is no formula). We could write this as $$b_n=K\left[\sum_{i=2}^n\frac{n}{i}\right]+nb_1$$
Finishing up
We could go back from this formula to a formula for \(u_n\); but he sees a slight improvement to make before we do that:
Ultimately, this is our answer. We notice that we might have gotten a simpler answer by considering b(n)/n, or half of that which is
v(n) = u(n)/(2n)!,
and that would have changed our recurrence (after some simplifying and rewriting) to
n+1
v(n+2) - v(n+1) = ---*(v(n+1) - v(n))
n+2
and therefore
v(n) - v(n-1) = M*1/n
for some constant M, and
n M
v(n) = sum --- + v(0).
i=1 i
Here is the work to get his recursion in \(v_n\), which I’ll do a little differently than I did \(b_n\). This time I’ll replace \(u_n\) with \((2n)!v_n\) before dividing everything by \((2n+3)!\):
$$u_{n+2}=2(2n+3)^2u_{n+1}-4(n+1)^2(2n+1)(2n+3)u_n\\(2n+4)!v_{n+2}=2(2n+3)^2(2n+2)!v_{n+1}-4(n+1)^2(2n+1)(2n+3)(2n)!v_n\\(2n+4)(2n+3)!v_{n+2}=2(2n+3)(2n+3)(2n+2)!v_{n+1}-(2n+2)(2n+3)(2n+2)(2n+1)(2n)!v_n\\(2n+4)(2n+3)!v_{n+2}=2(2n+3)(2n+3)!v_{n+1}-(2n+2)(2n+3)!v_n\\(2n+4)v_{n+2}=2(2n+3)v_{n+1}-(2n+2)v_n\\(n+2)v_{n+2}=(2n+3)v_{n+1}-(n+1)v_n\\(n+2)v_{n+2}=(n+2)v_{n+1}+(n+1)v_{n+1}-(n+1)v_n\\(n+2)(v_{n+2}-v_{n+1})=(n+1)(v_{n+1}-v_n)\\v_{n+2}-v_{n+1}=\frac{n+1}{n+2}(v_{n+1}-v_n)$$
If we define \(w_n = v_{n+1}-v_n\), this is a first-order recurrence, $$w_{n+1}=\frac{n+1}{n+2}w_n$$
What this tells us is that we are repeatedly multiplying (starting with \(w_0\)) by \(\frac{1}{2}\cdot\frac{2}{3}\cdot\frac{3}{4}\cdot\frac{4}{5}\cdots\frac{n}{n+1}\) which all cancels out and leaves \(w_n=\frac{1}{n+1}w_0)\). Absorbing constants into \(M\), we are left with $$w_n=\frac{1}{n+1}W\\v_{n+1}-v_n=\frac{W}{n+1}$$
Since this is the difference from one term to the next, we are adding all the terms to obtain the nth term: $$v_n=M\sum_{i=1}^n\frac{1}{i}+N$$ This is like our formula for \(b_n\), but without the n‘s that got in the way.
Now we can use \(v_n\) to find the formula for \(u_n\): $$u_n=(2n)!v_n=(2n)!\left(M\sum_{i=1}^n\frac{1}{i}+N\right)$$
In either case, we find that the general solution to your recurrence relation is
n (2n)!
u(n) = C sum ----- + D * (2n)!
i=1 i
for constants C and D. (Of course, you could start the sum at some other value by changing the constant D; so the 1 is sort of arbitrary.) You can also write expressions for C and D in terms of the initial conditions u(0) and u(1).
This can be written as $$(2n)!\left(C\sum_{i=1}^n\frac{1}{i}+D\right)$$
But there’s a problem when we try to use \(u_0\) and \(u_1\) to find the constants: We can’t let \(n=0\) in this formula, since the summation starts at 1. For this reason, when I first checked the result, I used \(u_1\) and \(u_2\). (This resulted in some oddities; in particular, my \(a_n\) were not all integers. That appears to be true only when \(u_1\) and \(u_2\) arise from the recursion, so that they have the right divisibility properties themselves.)
But if we take \(\sum_{i=1}^0\frac{1}{i}=0\), since we are adding no terms, it works out. We find that $$C=\frac{u_1}{2}-u_0\\ D=u_0$$
For our specific example, with \(u_0=1,u_1=3\), we get \(C=\frac{3}{2}-1=\frac{1}{2}\) and \( D=1\), so that the formula is $$u_n=\frac{(2n)!}{2}\left(\sum_{i=1}^n\frac{1}{i}+2\right)$$ I checked this out with a spreadsheet before starting this post, to make sure it was right, and it worked, no matter what I used for the first two terms. (I had to do the summations in their own column – recursively!) But as a manual example, $$u_2=\frac{(4)!}{2}\left(\sum_{i=1}^2\frac{1}{i}+2\right)=12\left(\frac{1}{1}+\frac{1}{2}+2\right)=12\left(\frac{7}{2}\right)=42$$ as we saw at the start.
This is a demonstration of perseverance, creativity, and insight – skills that can’t be learned by doing routine problems, but only by accepting challenges (and trusting that they can be overcome).
