Some recent questions have dealt with translation, rotation, and reflection of geometric shapes, so it may be time to look into what we have said about that in the past. Here we’ll look at the meaning of these terms, at levels suitable for both kids and adults, and next time we’ll see what happens when you combine them.
Rotation, translation, and reflection
We’ll start with this question, from 2005:
Rotation, Translation, and Reflection in the Plane Dear Dr. Math, Can you please help me? I don't know what these terms mean. rotate translate reflect I know they have to do with geometry but I don't know how exactly. Thanks for your help!
I answered:
Hi, Taylor. There are three ways you can move an object around in a plane without changing its shape or size. (The technical term for this is "isometry".) A rotation means turning it, like +---+ | | | | +-----------+ | | -----> | | | o---+ | o-------+ | | | | +-------+ +---+ Imagine sticking a pin in the object and spinning it by some amount.
It’s important to point out that a rotation depends both on where you stick the pin (that is, the point about which it rotates), and the angle through which it rotates. In my drawing, I put a pin at the “o” and turned the L 90° clockwise,
Here are rotations of two green L’s, both 60° clockwise, around two different points, resulting in the red shape:
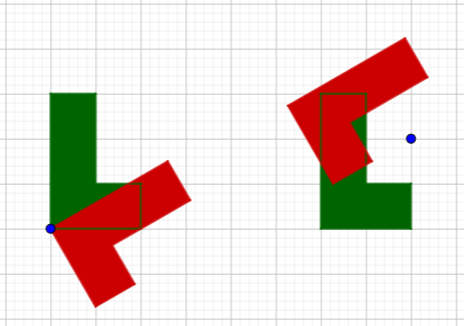
Note that the “pivot” (center of rotation) can be anywhere.
A translation just slides it, without turning:
+---+
| |
| | +---+
| | -----> | |
| +---+ | |
| | | |
+-------+ | +---+
| |
+-------+
A translation depends on the direction and distance of the motion, which can be described by a vector (or by amounts to be added to the x– and y-coordinates of every point).
Here are translations of two green L’s, using different arrows (vectors):
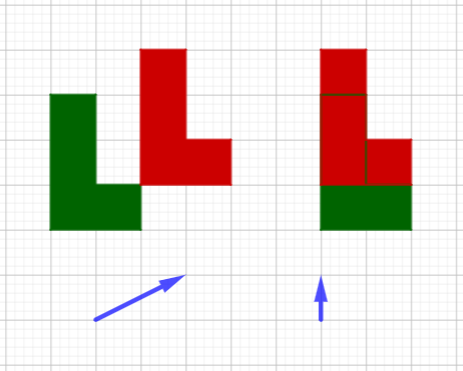
A reflection is like looking at it in a mirror; it flips the object over: +---+ +---+ | | | | | | | | | | -----> | | | +---+ +---+ | | | | | +-------+ +-------+ The "image" will be on the other side of the "mirror" line, the same distance away: +---+ | +---+ | | | | | | | | | | | | | | | | +---+ | +---+ | | | | | | +-------+ | +-------+
A reflection is defined entirely by the line across which the object is reflected. We’ll be seeing how “flip” is not quite the right idea, ultimately, but works as long as we are in two dimensions.
Here is one L, reflected across three different lines:
In each case, any point in the original “reflects” to a point opposite it, as shown by the arrows.
Slide, flip, and turn
The same concepts, with more child-friendly names, are the subject of this 2001 question:
Translation, Reflection, Rotation What is the difference between slide, flip, and turn? I find it really hard. What are shapes - can you send me a list?
A “shape” in this context (the things you are sliding, etc.) just means anything you can draw; it doesn’t have to be one of a list of basic shapes. The word also doesn’t refer to “shape” in the sense what kind of shape it is. You could just call them “objects”.
I answered, illustrating each from everyday life:
Hi, Mike.
Slide, flip, and turn are meant to be kid-friendly replacements for the technical terms translation, reflection, and rotation. You're supposed to be able to picture them more easily using the simpler words. So let's relate their math meaning to their everyday use.
If I SLIDE into home plate, I am basically moving sideways without turning. Here I'll slide a square from one side of the page to the other:
+-----+ +-----+
| | | |
| | | |
+-----+ +-----+
This only changes the shape's position (where it is), not its orientation (the direction it faces). Maybe there's a gyroscope inside the shape!
Objects in real life will often turn as they slide; here we’re separating the two ideas. (That’s something mathematicians tend to do!) We’re talking about something that only slides, and nothing else. And that’s why we have a technical term, “translation” (which comes from Latin for “carrying across”).
We’ll be using the word “orientation” in a different way later; here, it just means, as I said, the direction it points. Later, it will be something about the object itself. (Unfortunately, that’s also something mathematicians tend to do: use the same word in different ways. Or maybe that’s just something humans tend to do …)
If I TURN around, I pivot so that I face a different direction. Here I'll turn, or rotate, a square by about 45 degrees:
+
+---------+ / \
| | / \
| | + +
| | \ /
| | \ /
+---------+ +
A rotation doesn't change the shape, but it will change the position of parts of it, and the direction it faces. It's best to picture rotation as rotation in place, that is, imagine my first square as a piece of paper, put a pin through the middle, and rotate it round the pin, so the center of my second picture is actually in the same place as the center of the first.
I could have drawn it without sliding, but without color or better drawing tools, that would have been hard. Here I’ve slid it, and then turned in place as I described:
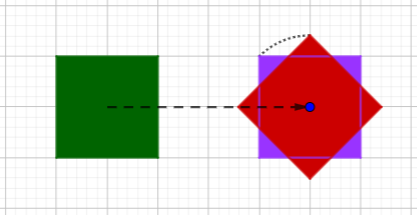
But in fact, the picture I made can be seen as a single rotation without sliding, if I put the pin far from the square:
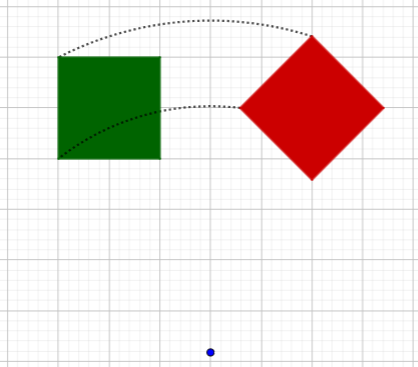
Put a pin in the blue dot and turn the page 45°. (We’ll see more about this next time.)
If I FLIP a pancake, I'm turning it over. The same sort of thing happens if I look at myself in a mirror; the left and right sides switch places. Here I'll flip a right triangle over:
+ : +
|\ : /|
| \ : / |
| \ : / |
+---+ : +---+
Notice that I can't make this same change by sliding or turning; if the triangle were a separate piece of paper, I would have had to turn it over. If I had to keep the same side on top, I would have to replace it with a new copy made backward; or I could just put a mirror along the dotted line and only see the reflection of the original triangle in the new position. You can also imagine turning (flipping) a page in a book; the dotted line is then the middle of the book.
If you need more help, you might want to send in a problem involving these motions, and tell me where you have trouble with it.
There are some subtle ideas hidden here. In particular, since flipping an object over changes what’s on top, that isn’t really the same thing as a reflection, unless we are thinking entirely in two dimensions. Flipping an object over is literally a rotation (in the air)! This is why “reflection” is a better name for it.
My brother Rick and I are “mirror twins” (with opposite handedness, and so on), which makes it easier for us to imagine this. There is a picture of us at around 5 years old where we are holding an empty picture frame between us, so one looks like the mirror image of the other. Standing next to one another, we couldn’t be “slid” into one another’s locations and match up; we are not the same object, but two different bodies, one with the hair naturally parted on the left, the other on the right. We’ll talk about “orientation” in this sense soon!

Unfortunately, the hats hide the reversed whorls in our hair.
Doing it on a computer
Here’s a different way to think about it, from 1998:
Flips, Reflections, Rotation, and Quadrants My daughter is in fifth grade. The terms quadrants, reflections, flips, and rotation are being used to describe the movement of shapes. I have no idea what they are talking about and neither does she. Any ideas?
Doctor Rick answered:
Hi, Roger. Do you have a computer drawing program? These terms, except perhaps for "quadrant," can probably all be found there, and this could be a good way to gain an understanding of the concepts. In many drawing programs, you can create a shape with something like a "polygon tool." Then, while the shape is selected, you can go to a menu and find commands "flip," "reflect," and "rotate." Some programs might use different terms, and not every program can do free rotation, so I'll describe them.
I’ll be demonstrating these actions by making multiple copies of the same shape, and then transforming some of them as indicated.
"Flip" is a (not very technical) term for switching the top and bottom of a figure. Imagine attaching a horizontal rod across the middle of the shape, then rotating the figure half a turn about the rod. The top is now on the bottom and the bottom is now on the top. "Reflect" refers to what you see when you look in mirror: your left hand becomes the right hand of the reflection, and your right hand becomes its left hand. So we often use the word "reflect" to mean the same thing as "flip" except that the imaginary rod on which you turn the shape is vertical this time rather than horizontal. In more technical use, a "reflection" can be about any axis, horizontal or vertical or at any angle.
To my knowledge, in both math and computer programs, these words are synonymous, and can both refer to reflection over any axis. But what he says is probably more or less true elsewhere, that we tend to think of flipping something upside-down, but reflecting horizontally.
Programs commonly have “flip” (horizontal and vertical) in their menus. Here is the menu in Microsoft Word’s Shapes tool, as a simple example:
In a more sophisticated drawing program, there will be different tools. I made most pictures here using GeoGebra as a geometrical drawing tool; here is its “Transform” menu:
Here I made three copies of an L shape in Word, one green and two red, and applied “Flip Vertical” and “Flip Horizontal” to the latter, respectively:

Vertical and horizontal refer to the direction of motion; the direction of the reflecting line is perpendicular to the motion. The line is always taken to be through the middle of the object.
"Rotate" simply means to turn the shape, just as if you drew the shape on paper, put the paper on the desk, and turned the paper.
Word and Paint both have “rotate” (right, left, or other angles) in their menus. Here I again made three copies of an L shape, and applied “Rotate Right 90°” and “Rotate Left 90°” to the latter:

Each was rotated around its center.
For “free rotation”, it is common to have either a dialog where you enter an angle, or a “handle” to rotate the object:
By the way, what does translation (sliding) look like in a computer drawing? It’s commonly called “dragging”, and doesn’t need a menu, just a handle to drag. (I can’t catch that in a picture!)
After a little talk about quadrants, he concluded:
Everything I've said is about two-dimensional shapes (shapes you can draw on paper). My description of reflection is wrong in 3 dimensions: it isn't rotation on an axis as I described it, but reflection in a plane (like a mirror). In two dimensions, these two actions are the same. I hope this has helped. If you have a drawing program that has these functions, it will be a big help to your daughter - but you can do the same things by just cutting a paper shape and turning and flipping it.
Orientation-preserving transformations
Here’s a 2007 question about a property of some transformations:
Explanation of Orientation in Transformations We've been learning about transformations; translations, reflections, rotations, and dilations, and my teacher keeps saying that a translation, a rotation, and a dilation preserve the orientation. I'm confused as to what orientation is. I think it has to do with naming the triangle. My teacher has mentioned about naming them clockwise or counter-clockwise. I've looked for it in our book, but it's not explained. Could you help?
Here we have one additional transformation mentioned, the dilation. The others all preserve size as well as shape, which is the meaning of “isometry”; dilation (stretching evenly in all directions) preserves shape but not size. But here, the question is about what makes reflection different: What is this “orientation” that reflection “doesn’t preserve”?
I answered:
Hi, Laura.
Imagine making a triangle out of paper that is, say, white on one side and black on the other. Avoid making it isosceles. Here's mine:
A
\ \
\ \
\ \
C---------------B
Now if you slide it around (translate it) or turn it (rotate it), or look at it through a magnifying glass (dilate it), it will still have the white side up, and if you go from A to B to C you will still be going clockwise.
If I had named the vertices in the opposite order, then no matter what you did, they would always be counterclockwise.
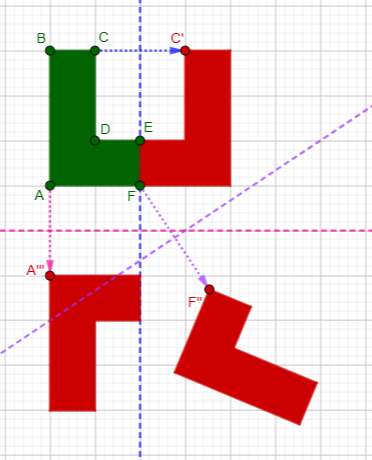
Here I made the green triangle, and translated it (magenta) using the vector DE, then rotated it by 60° around point F (orange), and then dilated it by a factor of 2 from F (red):
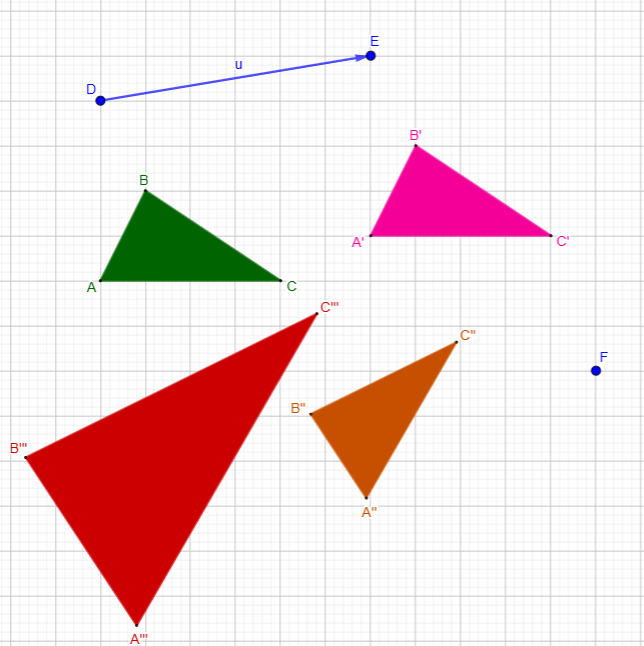
All of those transformations preserved the orientation, which remains clockwise.
But now reflect it, say in a vertical line. You can only do that with your model by flipping it over (so the black side is now up):
A | A
\ \ | /XXX/
\ \ | /XXXXXXX/
\ \ | /XXXXXXXXXXX/
C---------------B | B---------------C
We can see in two ways that its orientation is different: we had to turn it over; and when we go from A to B to C now, we are going counterclockwise. And that difference is what we call "orientation".
Here I’ve reflected the same triangle:
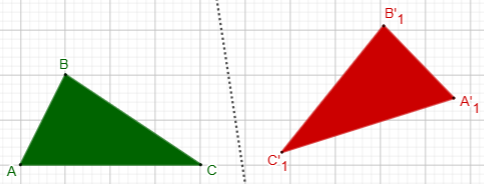
As we’ve seen, of course, flipping it over isn’t reflection in a 3D sense. True reflection doesn’t change the color; it just changes the order, while still keeping the white side on top! Flipping it over only simulates reflection.
If we were talking about transformation in 3D space, then we would consider these two triangles as still having the same orientation, because we could go around to the back of the paper (or screen, in our imagination) and still see it clockwise. We’d identify orientation not by mere “clockwise-ness”, but by a 3D feature called “handedness”. I won’t try to explain that here. But you can picture it with my mirror-twin picture.
But …
We’ll close with an interesting question from 2003:
Reflection and Rotation I am a math teacher. I have a strong math background but not for these topics. Can rotation of a figure and reflection of that same figure yield the same result at times? If a shape with one line of symmetry, such as a club (from playing cards), is reflected across a line, this same image could be obtained by rotating the shape, right?
We’ll be looking at “lines of symmetry” more in a later post on symmetry, but you’ll get the idea.
I answered:
Hi, Anita. I think you are talking about something like this:Here I drew a T and an L, and reflected both across a line. The image of the L clearly can be obtained only by reflection; but the T image can also be obtained by rotation about a point on the line, as shown.
You can’t move the reflected L (by translation or rotation) so that it would match the original L; the orientation has been changed.
But the reflected T is identical to the original, because T is symmetrical. That means it can be rotated back into place.
The reason for this is that any rotation or translation is equivalent to two reflections; when the object has a reflection symmetry, a single reflection produces the same effect as that reflection followed by a reflection in its line of symmetry, and so is equivalent to a rotation; specifically, it will be a rotation about the point of intersection of the line in which it was reflected, and the line of symmetry (of both the original object and the image).
We’ll talk about combining transformations next time, and see how this is true.
So if a problem asks for any transformation that will take the first T into the other, you can use either the reflection or the rotation. Of course, if the corresponding points on the original and the image were marked, that would force you to choose either the reflection or the rotation.
Anita replied,
Wow! That was a prompt response! Thank you so much. I especially like the illustration. Yes, that's exactly what I meant. You were very helpful.
Next time, we’ll look at combining transformations; in particular we’ll see the fourth isometry, the glide reflection, which is really just a combination of translation and reflection (flip-slide).

Pingback: Slides, Turns, and Flips: How to Combine Them – The Math Doctors
Pingback: From Transformations to Symmetry – The Math Doctors
Pingback: Trouble with Transformations – The Math Doctors