Continuing to look at past questions that didn’t make it into the blog, I find a question about percentage change in temperature, which nicely ties together a couple older topics that have long been on my list to cover. Let’s do that now.
Why doesn’t percent change work for temperature?
Here is the question, from P. W., in May 2023:
Middle school students can readily determine that a price rise from $50 to $68 is a 36% increase. They are likely to regard a temperature rise from 50°F to 68°F as a 36% increase as well.
They are likely then to be at a loss to explain what’s wrong when they carry out the calculation for the corresponding rise from 10°C to 20°C, which appears to be a 100% increase.
What suggestions have you as to how to explain, from as fundamental a point of view as reasonable, why there is no such problem (say) if the price increase is figured in Euros, and most important, how to remedy the situation with respect to temperature so that a temperature change can be characterized in some suitable way. I would be nice if, armed with your explanations, a student might be able to explain it to a student who missed the class.
We discussed percent change in a series beginning with Percent Change: Finding and Applying It, where we define it as $$\text{percent change}=\frac{\text{new }-\text{ old}}{\text{old}}\times100\%.$$ If the old price is $50 and the new price is $68, then $$\text{percent change}=\frac{68-50}{50}\times 100\%=\frac{18}{50}\times 100\%=36\%.$$ We could do exactly the same thing when the old temperature is 50°F and the new temperature is 68°F, and get the same answer.
But if we convert to Celsius, using \(C=\frac{5}{9}(F-32)\), we find that the two temperatures are \(C(50)=\frac{5}{9}(50-32)=10\) and \(C(68)=\frac{5}{9}(68-32)=20\), and the increase is now $$\text{percent change}=\frac{20-10}{10}\times 100\%=\frac{10}{10}\times 100\%=100\%.$$ So the percent increase depends on what units we use!
If we converted $50 and $68 to Euros, the percent increase would not change. At this moment, it would be $$\text{percent change}=\frac{66.01-48.53}{48.53}\times 100\%=0.36\times 100\%=36\%.$$
Something seems to be wrong with temperatures, when calculations that don’t depend on whether the unit is $ or € do depend on whether it is °F or °C. How to explain it?
The problem of units
Doctor Rick answered:
Hi, P. W., thanks for writing.
It took me a while to realize the exact point you’re making: that 50°F = 10°C, and 68°F = 20°C, and therefore one might naively expect the ratio of 50°F to 68°F to be the same as the ratio of 10°C to 20°C. It is surprising that the percentage increase we calculate depends on the system of measurement we’re using.
You know the cause of this oddity, right? You’re asking how we would explain it to a Middle Schooler.
We’ll see that this is not all that P. W. had in mind; but it is an important piece of it. We’ll be looking for the underlying problem in temperature when it comes to percent calculations, and the issue of units helps to reveal it.
The unusual feature of degrees Fahrenheit and Celsius is that we are not just talking about different units, but also different starting points: 0°F is not the same temperature as 0°C. That’s why we don’t just have a conversion factor between °C and °F, as we would between, say, feet and meters:
F = 3.28M (F = length in feet, M = length in meters) [1]
Instead, we need a conversion formula, which is a linear equation.
F = 1.8C + 32 (F = Fahrenheit temp, C = Celsius temp) [2]
The graph of the relation between feet and meters is a straight line that passes through the origin; any ordinary conversion works this way. However, when you graph the relation between Celsius temperature and Fahrenheit temperature, you get a line that does not pass through the origin!
Here are those graphs. First, meters to feet:
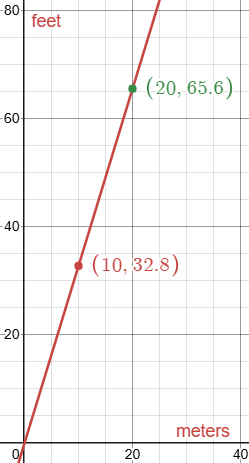
Here, the ratio of feet to meters is always equal to the slope of the line. And since, in this example, $$\frac{65.6}{20}=\frac{32.8}{10},$$ it is also true that $$\frac{65.6}{32.8}=\frac{20}{10}.$$ So the number of feet is proportional to the number of meters, and the ratio of two temperatures is consistent.
Second, Celsius to Fahrenheit:
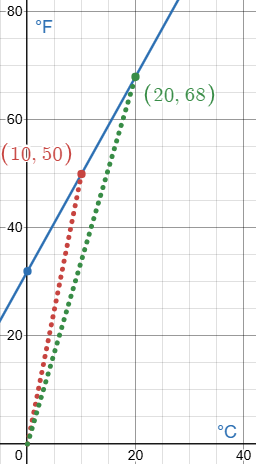
Here, the ratio of F to C is the slope of a line from the origin to a point on the graph, which varies, as shown by the dotted lines; in fact, it would be infinite at \(0^\circ C\). And since this time we can’t say that $$\frac{68}{20}=\frac{50}{10},$$ it is also not true that $$\frac{68}{50}=\frac{20}{10}.$$ So the temperature in °F is not proportional to the temperature in °C, and the ratio of two temperatures is not consistent.
In such a situation, the ratio of two quantities is not meaningful. However, the ratio of two temperature differences is still meaningful. For instance,
The difference between 50°F and 68°F is half the difference between 50°F and 86°F.
The statement is still true when I replace Fahrenheit temperatures with Celsius temperatures:
The difference between 10°C and 20°C is half the difference between 10°C and 30°C.
Why is this? When we consider temperature differences, the zero point is irrelevant; only the “size” of a degree matters. If I convert the difference, 20°C – 10°C = 10°C, to Fahrenheit, I get
1.8(10°C) = 18°F
which is just the difference 68°F – 50°F. Note that in this conversion, I did not add 32°! In graphing terms, the factor 1.8 is the slope of the line plotted from equation [2] above — it’s the ratio of the sizes of the two kinds of degree. When I add 1°C to a temperature, I add 1.8°F.
When we talk about a change from one temperature to another, we are in effect choosing our own “zero point”, so the ratio of two changes is independent of the units we use, just like for lengths. On the other hand, a percent increase in temperature means an increase in how much warmer it is than the zero of our chosen scale. Changing that changes our percentage.
Absolute units make it meaningful
The zeros in the Fahrenheit and Celsius scales are chosen arbitrarily. There is, however, such a thing as absolute zero; it has real meaning in physics. The Kelvin temperature scale uses Celsius degrees but a different zero point: 0°K (officially called 0 K) is -273.15°C. There is also a scale that uses the Fahrenheit degree but puts the zero point at absolute zero; it’s called the Rankine scale. Conversion between Kelvin and Rankine scales is just a matter of multiplying by a factor; if one temperature is twice another on the Kelvin scale, then it is also twice the other on the Rankine scale.
So Kelvin and Rankine are like Celsius and Fahrenheit but sharing the same zero – and this zero has real meaning; temperature in these scales is proportional to energy.
In the Ask Dr. Math Archive, we have several answers, not to your exact question (no mention of percentages), but to a related question — one that is perhaps even more perplexing than the one you raise: “What is twice as cold as zero?”
If you do not already have an account with NCTM (the National Council of Teachers of Mathematics), you can get one free, so you will have access to the pages above. There you will see that we tried to grapple with the meaning of “twice as cold” (or “twice as hot”) — it certainly isn’t the same as “twice as far from zero”, which is what the question assumes. The matter of Fahrenheit versus Celsius is mentioned, but it isn’t the only issue.
Let’s look at these two pages here, because they are very relevant to the question. If there is a 100% increase in temperature, then the new temperature must be 200% as high, so it will be twice as hot. Right? Or not?
Twice as hot? It’s relative
This question comes from 2007:
Doubling Zero? I have a student who asked, "What is twice as cold as zero?"
Doctor Ian answered, starting with “twice as hot”:
Hi Claire, It's not really a sensible concept, because temperature is a relative measurement, not an absolute one (like length, or mass). What you CAN sensibly ask is something like: In the _____ scale, what temperature is twice as far from zero degrees as _____ degrees? For example, it makes sense to say that In the Celsius scale, 48 degrees is twice as far from 0 degrees as 24 degrees.
Here, “twice as hot” has been replaced with “twice as far from zero”.
But that doesn't make it "twice as hot". When asked this way, you can say that In the Celsius scale, 0 degrees is twice as far from 0 degrees as 0 degrees. But this doesn't mean that 0 is "twice as cold" as zero. The real lesson here is that just because you can form a question that is grammatical, that doesn't mean the question makes sense, or has an answer.
Similarly, if I asked, “What mountain is twice as high as Pike’s Peak?”, you would give different answers depending on whether you meant altitude above sea level, or above the surrounding landscape – or above the center of the earth! The question as stated would be meaningless.
Twice as warm? Use Kelvin
We got the same question from Daniel in 1999:
Twice as Cold as Zero I've asked and wondered about this a lot but have found no good answer so far. What is the temperature if it's twice as cold [or warm] as zero degrees?
Doctor Nbrooke answered:
Hello, and thanks for writing to Dr. Math. You pose a very interesting question. What is the temperature if it's twice as cold as zero degrees? The Fahrenheit and Celsius temperature scales are "relative" temperature scales, in that they are both relative to a couple of specific temperatures, namely the freezing and boiling points of water. Let's make your question a little more specific: "What is the temperature if it's twice as warm as 0 degrees Celsius (the freezing point of water)?" To answer this question we need to convert this Celsius temperature to an "absolute" temperature scale, a scale with no negative temperatures. We'll use the Kelvin scale. 0 degrees Kelvin is the point at which all motion in matter stops; it is known as "absolute zero." No temperature can exist that is lower than 0 degrees Kelvin. The formula to convert from Celsius to Kelvin temperature is K = C + 273.15, where K is the Kelvin temperature and C is the Celsius temperature. So 0 degrees Celsius is equal to 273.15 degrees Kelvin. We can double this number to get 546.30, the temperature that is twice as warm as 0 degrees Celsius. We can then subtract 273.15 from our answer to convert it back to the Celsius scale. The temperature is 273.15 degrees Celsius when it is twice as warm as 0 degrees Celsius. Makes perfect sense, doesn't it?
Implicitly, he has defined “warm” as the amount of energy; if you double the temperature (Kelvin), you have doubled the heat energy (all other things being equal). So, yes, this does make sense.
I’ll omit an additional question included there, specifically dealing with the question of what it means (if anything) for one temperature to be twice as cold as another, which adds even more confusion. I think it’s worth reading.
Percentage change from a negative or zero value
P. W. wrote back, changing the focus from inconsistency between units to another issue:
Thanks for your reply.
Celsius vs Fahrenheit was an unintentional red herring. Properties of the conversion between °C and °F are not fundamental to my question. I apologize for sending you away from what I was driving at.
Fahrenheit on its own gives nonsense percentage changes, e.g., from 0°F to 80°F (% change undefined) or from -40°F to (+)40°F (% change = –2). Celsius has the same defect, on its own. Prices in dollars or in Euros do not.
My question is then slightly different: what is it about (say) Celsius that makes it illegitimate here, while the Euro is perfectly OK? And, in effect, why has this problem never appeared before in the student’s experience? What fundamental property do all the OK situations have that °F and °C do not? Is it just that OK quantities have a zero, and that only positive values make any sense?
Bottom line, what is required of any quantity if it is to be suitable for percentage change calculations? (Fractional changes are more fundamental than % changes, so one can focus on them.) I’m tending in that direction for my “what to tell the student” bottom line, but I’m not yet confident of it — your experience is far deeper than mine, and I’d like to hear more from you on this.
And thanks for your time and expertise.
The discussion of units was perhaps more relevant than he sees, because the zero point is central (no pun intended) to both issues.
I joined in, with a suggestion:
My own thought is that this is largely about temperatures being an interval scale, rather than a ratio scale:
https://onlinestatbook.com/2/introduction/levels_of_measurement.html
https://en.wikipedia.org/wiki/Level_of_measurement
The fact that the zero point is not inherently meaningful (except for Kelvin) means that ratios (such as percentages) are not meaningful.
This idea is closely related to what we later discussed in
Types of Data: Discrete, Continuous, Nominal, Ordinal, …
The concept of “levels of measurement” is that variables in statistics can be divided into four increasingly meaningful categories. Here is an excerpt from that post:
- Nominal data merely gives a name to a category; in statistics, this is usually not a number, but something like male/female, colors, or states. The important thing is that, even if it’s a number, no arithmetic performed on it would make sense. All you can do is ask if they are the same (=).
- Ordinal data gives some sort of order or rank to an item; this might be a number (such as the number of stars in a movie review, or pain ranked on a scale from 1 to 10), or it might just be words (low/medium/high, or very unsatisfied/unsatisfied/neutral/satisfied/very satisfied) that might be encoded as a number. Again, no arithmetic calculations would make sense; but we can compare them (<, >).
- Interval data is numerical data in which not only the mere order, but the amount of difference between numbers, is meaningful. The classic example is temperature scales such as Celsius, where a difference of 10 degrees, say, has a specific meaning regardless of the temperature, but 0 has no real meaning, so you can’t talk about something being twice as hot as another (though a temperature difference may be twice as much as another). … This means that addition (as in finding an average) and subtraction (of two values) make sense (+, -).
- Ratio data goes beyond interval data in having a meaningful zero. Most measurements we make, like height, length, and weight, are this type, since zero means there is no height, length, or weight. Here, multiplication (by a scaling factor) and division (by one another, to find a scaling factor) make sense (×, ÷).
Doctor Rick concurred:
No problem, this question is interesting too!
I almost included a reference to “levels of measurement” as Doctor Peterson did; that is surely at the heart of both issues.
The direct answer to the original question is simply that temperature is not a “ratio level” measurement, so ratios (and percentages) are inappropriate. But even with money, there are situations where negative values can occur, and get in the way. (And a percent increase from zero is infinite, even for money!) That leads to another topic:
We had considerable discussion on the old Ask Dr. Math about situations in which percentage change doesn’t make sense, or else we have to work hard to find some sense in it. It appears that this has not made it into a Math Doctors blog. I don’t recall that this was ever related to temperatures, but any quantity that can be negative (or zero) can cause problems. A common example is profit. If a company had a $10,000 loss (-$10,000 profit) last quarter and a $5,000 profit this quarter, the calculation for percentage change in profit is:
(5000 – (-10,000)) / (–10,000)×100% = –150%
Is that a 150% decrease in profit? But we made a lot more money this quarter! It doesn’t make sense.
See these items from the Ask Dr. Math Archives:
Calculating Percent Change when the Base is a Negative Number
We’ll look at these next time, because they are too long to fit here.
P. W. replied:
The cited paper on scales, which directly addresses the Fahrenheit scale as an example of one not suitable for such comparisons as percentage changes is just what I wanted. I will do the remaining work of addressing the middle-schooler rather than the research psychologist.
This will also allow me to inject the notion that physics, when the student gets there, will make it clear that there is indeed a fundamental zero to temperature, so that percentage changes in temperature can make sense.
Thanks for the help both of you have provided.
Summarizing how this all fits together:
- Celsius and Fahrenheit have arbitrary zero points that have no inherent meaning.
- On one hand, this is why ratios between temperatures depend on what scale you use.
- On the other hand, it is also why these are interval scales; that is, ratios (and percentages) are not meaningful.
- Also, those zero points permit temperatures to have negative values, where percent change would be, to say the least, hard to interpret.
- This is true not only of temperatures, but of some situations involving money. More on that next time!

Pingback: When Percentages Don’t Make Sense – The Math Doctors