Last time, we saw how Newton’s method works. Here, we’ll look at a question about why it might not work, which will lead to a deep examination of how iterative methods work in general, from which we will discover why Newton’s method is as good as it is. I have to say, as I read through this answer actively, trying out examples and making graphs to illustrate it, I came to appreciate the answer more and more.
What about arctan or cube root?
The question came to us in 2009:
Newton-Raphson Method Are there any equations that cannot be solved using the Newton-Raphson method (irrespective of the initial estimate)? I thought arctan(x) = 0 might not be solvable but one just needs to choose an initial value within about 1.39 of the root. I tried cube root of x = 0 and it seems that Newton-Raphson always diverges away from the root irrespective of the initial estimate (other than x = 0 of course). Is this correct? I am struggling with proving algebraically that Newton-Raphson always fails with cube root of x = 0. I would also like to solve what the critical value (for the first estimate) is for solving arctan(x) = 0 using Newton-Raphson (i.e. when does it diverge away and when does it converge to the root).
The Newton-Raphson method is another name for Newton’s method, emphasizing the fact that Isaac Newton himself did not formulate the method as we know it today.
Here is the graph of \(\arctan(x)\), showing how Newton’s method converges if we start at 1.33, just below William’s suggested boundary of 1.39:
And here we see it diverge when we start from 1.42, just above that boundary:
William has observed that for some equations like this one, you have to choose the initial guess carefully or it will fail (as we saw last time), while for others (as we’ll see below) there may not be any initial guess for which it will work. What makes the difference? And how can we know when it will converge?
Doctor Jacques answered:
Hi William,
It is correct that you cannot solve x^(1/3) = 0 by Newton-Raphson: the derivative of x^(1/3) is x^(-2/3)/3, and the iteration formula becomes:
x' = x - x^(1/3)/(x^(-2/3)/3)
= x - 3x
= -2x
and it is clear that this diverges if you start with any non-zero value of x.
(I have corrected a very minor sign error.)
He’s using \(x’\) to represent the next approximation, not a derivative; so whatever guess you have, the next will be twice as far from zero and on the opposite side. As we iterate this (repeat the same process), it clearly can’t approach zero, ever.
Here is what this looks like:
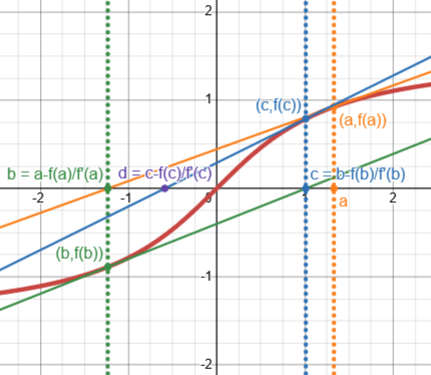
The red curve is the cube root; my initial guess is \(a=0.05\) (yellow); we follow successive tangents to get to \(b=-0.1\) (green), \(c=0.2\) (blue), and \(d=-0.4\) (purple). Rather than converging, the distance from the correct solution doubles at each step, alternating sides. It doesn’t converge, and never will for any initial guess, (Aren’t we lucky to already know that the solution is zero?)
(Incidentally, it is only when you are trying to find when the cube root is a number close to zero that Newton’s method fails; if we were solving, say, \(\sqrt[3]{x}=4\), it would converge easily.)
Exploring iteration in general
We’ll get to Newton’s method, but first we need some more general background.
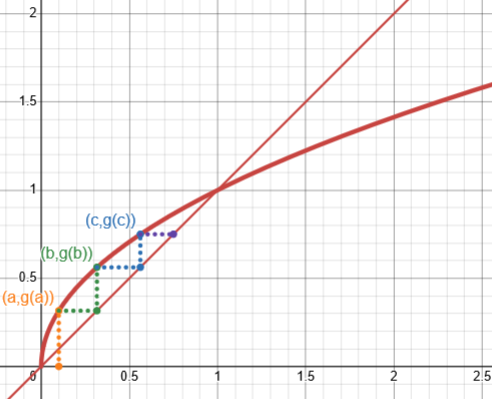
I don't know if it is possible to give a precise set of rules for the convergence of the N-R method; however, we can explore some related ideas and try to shed some light on the subject. It may be useful to study first another iterative method. Assume that we want to solve an equation of the form: x = g(x) [1] We might try to start with an initial guess x[0], and compute successive approximations by the formula: x[n+1] = g(x[n]) [2] If the sequence x[k] converges to some limit a, then a is a solution of [1], i.e. a = g(a). For example, if we want to solve the equation x = sqrt(x) (near 1), and if we start with an initial guess of 2, this procedure gives the sequence of values: 2.0000 1.4142 1.1892 1.0905 1.0443 which converges (very slowly) to 1.
Since convergence means that the successive values are very close, clearly in the limit, with the same number on both sides of \(x_{n+1}=g(x_n)\), we have \(x=g(x)\), a solution of the equation. In this example, with \(g(x)=\sqrt{x}\), we are solving \(x=\sqrt{x}\), whose solutions are \(x=1\) and \(x=0\), since \(x-\sqrt{x}=0\) can be factored as \((\sqrt{x}-1)\sqrt{x}=0\).
The interesting fact about the equation [1] is that it has a nice geometrical interpretation: each solution is an intersection of the curve y = g(x) and the line y = x. The algorithm [2] also has a geometrical interpretation. We start with an initial value x[0], and find the corresponding point on the curve y = g(x). From that point, we draw a horizontal line to the 45� line y = x. The x-coordinate of the intersection is the next approximation x[1] (try it, it is not very easy to draw this in an e-mail...). You will see that, if the sequence converges, you get either a staircase pattern or a "square spiral", depending on whether g(x) is increasing or decreasing. If the sequence diverges, you get the same pattern in reverse, i.e., the points get further apart from the solution.
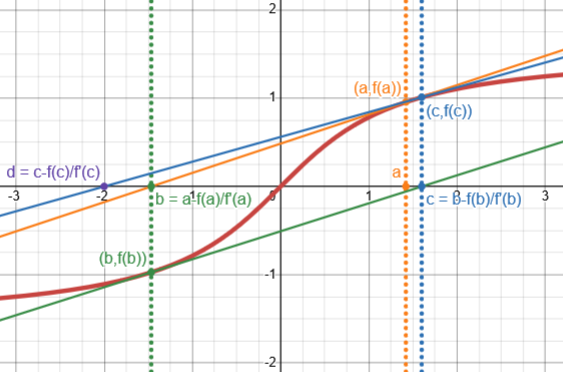
Here is what this process looks like graphically for the square root:
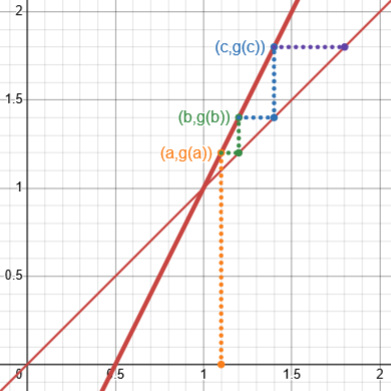
If we start closer to 0, we might expect to approach the other solution, \(x=0\), but it doesn’t:
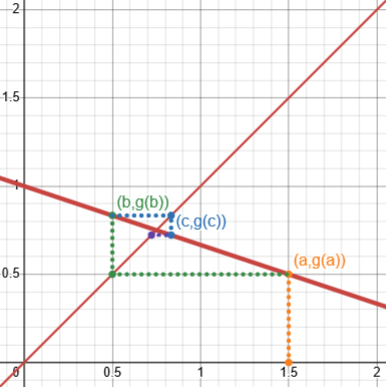
The problem is that the procedure may not converge. For example, if you try it with the equation: x = 2x - 1 (whose solution is x = 1), and start with an initial value close to 1, like 1.1, you will notice that the sequence x[n] diverges.
Here is the iteration for \(g(x)=2x-1\), showing how the iteration diverges:
Here is an example for a decreasing function showing convergence by a “square spiral”; here \(g(x)=1-\frac{x}{3}\):
But sometimes it can diverge in interesting ways; here is \(g(x)=2-x\):
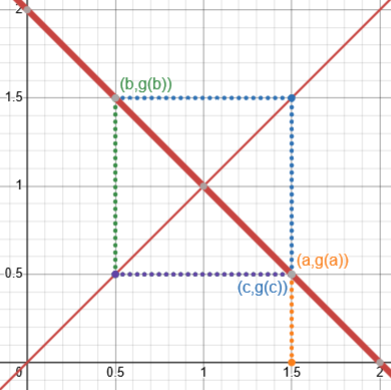
This just keeps cycling through two values.
The same is true for \(g(x)=\frac{1}{x}\):
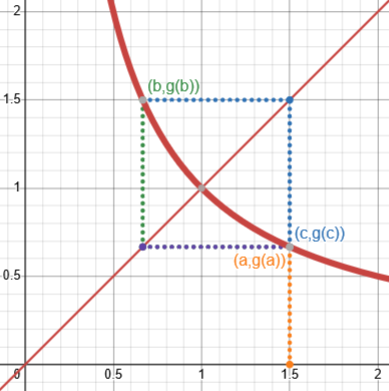
When will an iteration converge?
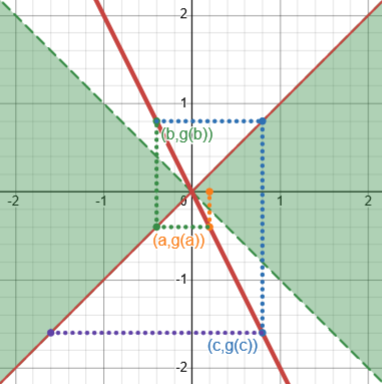
To find a sufficient condition for convergence, we draw two lines at (+/-) 45° from the solution point (a, g(a)). One of these lines is y = x, the other one is perpendicular and has equation y - g(a) = -(x - a). These lines divide the plane in four regions. We call the left and right regions "good" and the top and bottom regions "bad". The main result is that, if there is a neighborhood of a such that the graph of y = g(x) is entirely contained in the "good" region in that neighborhood, and if you start with an initial value in the neighborhood, the sequence x[n] will converge to a. Note that this is only a sufficient condition: if the condition is not satisfied, anything can happen. (If there is a neighborhood of a such that the graph of y = g(x) is entirely in the "bad" region in that neighborhood, then the sequence cannot converge "smoothly" to a, although you might still stumble on the solution by accident, depending on the behavior of g(x) outside the neighborhood).
A sufficient condition means that when we know it is true, we can be sure the associated fact is true; when it is not also a necessary condition, the fact can be true without it. Being in the “good region” is not the only way an iteration can converge, but it does imply that it will (for some starting values). See Necessary and Sufficient Conditions: If, or Only If?
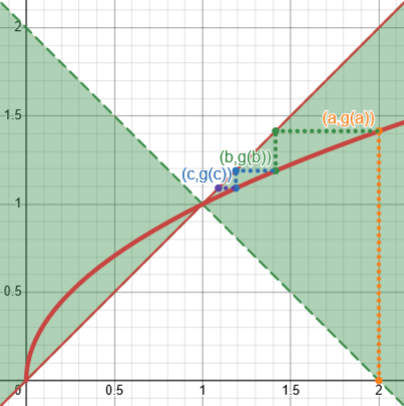
Here is our first example, \(g(x)=\sqrt{x}\), showing that the curve is entirely within the good regions (and, as we’ve seen, the iteration converges):
Here is our last example, \(g(x)=\frac{1}{x}\), showing that it is not:
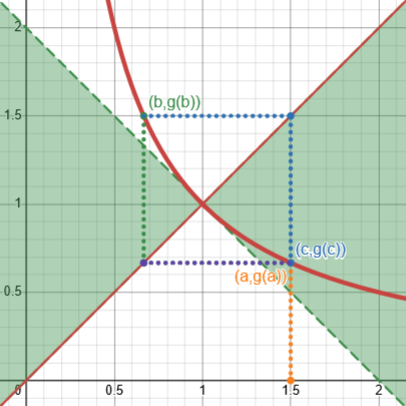
Again, not satisfying this condition does not imply that it won’t converge, but it does permit it to fail!
This can be proved rigorously (it is not very hard), but it can be seen easily by looking at the graph. In doing so, you will also notice that the convergence will be faster if the graph of g is closer to the horizontal.
Observe that in the convergent example above, each step results in a new value that is closer than the previous one, because the curve is below \(y=x\) and above \(y=-x\).
Now, it is a standard result of analysis (a variation of Rolle's theorem) that a _sufficient_ condition for the graph to be contained in the good region is that there exists a positive real number L < 1, such that |g'(x)| <= L in the neighborhood in question, where |g'(x)| is the absolute value of the derivative of g(x). (Note that it is not enough to have |g'(x)| < 1 : L must be fixed). To summarize: If there is a neighborhood of a such that |g'(a)| < L in that neighborhood, where L is positive and < 1, then the procedure [2] will converge to a for any initial value in the neighborhood in question. Note that this also is merely a sufficient condition. Using a previous remark, you will also expect that the convergence will be faster if L is smaller.
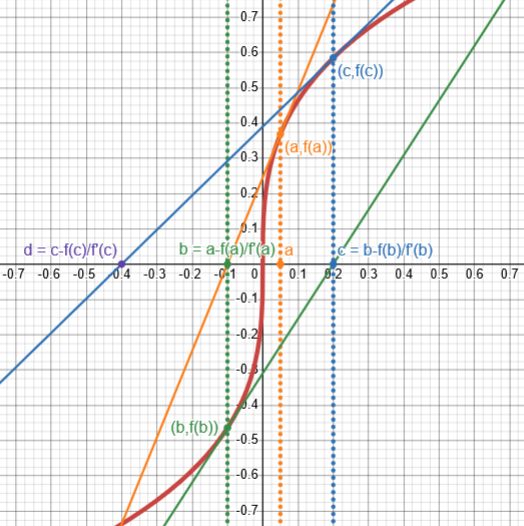
Here, for example, is \(g(x)=3(x-1)^3+1\), which converges for \(x=1.5\), but not for \(x=1.6\):
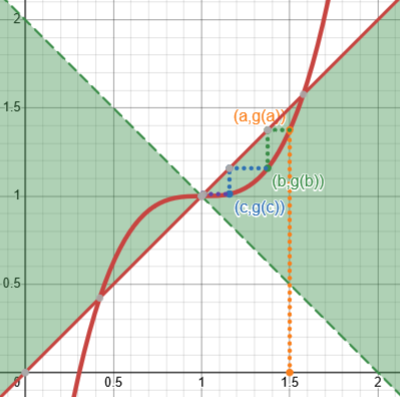
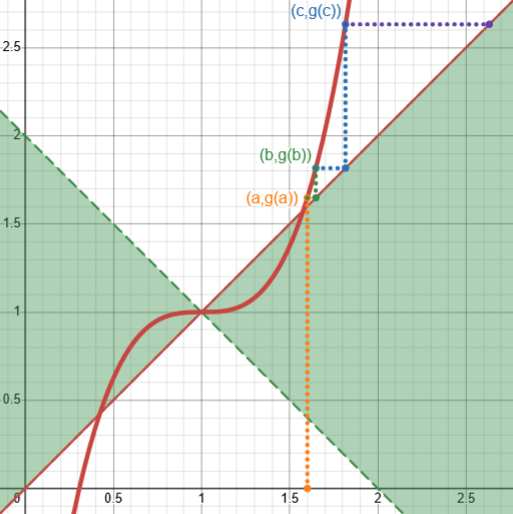
You may notice that the first iteration converges despite not being in the region where the derivative is less than 1 (since the slope at \(x=1.5\) is greater than 1), demonstrating that that, too, is only a sufficient, not a necessary, condition.
Applying this to Newton’s method
Now, Newton’s method involves iteration. How might we have invented an efficient iterative method to find roots of a function, given what we now know about how iteration works?
Given an equation: f(x) = 0 [3] there may be many ways to convert it to the form [1]; some of these ways will lead to convergent sequences, and some will lead to divergent sequences; in addition, the speed of convergence may be different depending on the form you select. For example, the equation x = sqrt(x) that we encountered previously can also be written as x = x^2. In this latter form, the algorithm [2] will never converge to the root x = 1 : if the initial value is > 1, the sequence diverges and if the initial value is < 1, the sequence converges to the other root x = 0.
Recall that form [1] was \(x=g(x)\), and [2] was the iteration \(x_{n+1}=g(x_n)\). What we want to do is to find zeros of a function, which means solving form [3], \(f(x)=0\).
The iteration for \(x=\sqrt{x}\) always worked well; but if we just square both sides, we get \(x=x^2\), which is not so well behaved. Here is what happens when we start at, respectively, \(x=0.75\), converging toward zero, and at \(x=1.05\), diverging:
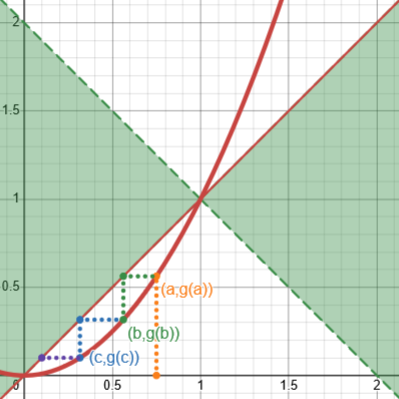
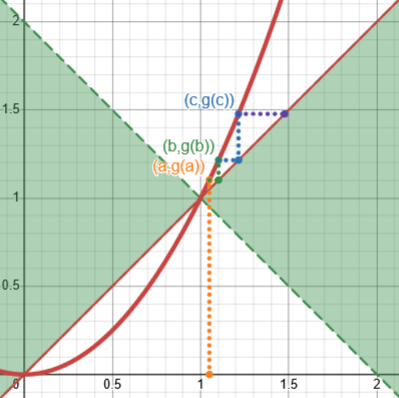
We can think of our iteration of \(g(x)=\sqrt{x}\) as an attempt to solve the equation \(\sqrt{x}-x=0\), by adding x to both sides and iterating. But we see here that if we did the same thing to try to solve \(x^2-x=0\), we would not get the solution we want. So we can’t blindly let \(g(x)=x+f(x)\) and use iteration to find when \(g(x)=x\).
And what makes these two functions behave so differently? The derivative of \(g(x)=\sqrt{x}\) is less than 1 at the point of interest, putting the curve in the “good” region, so the iteration converges; while the derivative of \(g(x)=x^2\) is greater than 1, so iteration diverges (from the desired solution).
Now, how does all this relate to Newton’s method? It turns out to be an example of the sort of iteration we’ve been examining, but carefully designed to converge quickly.
One possible way to convert an equation [3] to the form [1] is to write it as:
g(x) = x + a*f(x) [4]
which means that we take g(x) = x + a*f(x) for some constant a. As we have seen, the convergence will be faster if we can make |g'(x)| as small as possible in some neighborhood of the root. We have:
g'(x) = 1 + a*f'(x) [5]
If the derivative f'(x) is approximately equal to some constant k in the vicinity of the root, a good choice for a would be -1/k, since this will make g' approximately 0. If we guess k as f'(x), this gives the iteration formula:
x[n+1] = g(x[n])
= x[n] + a*f(x[n])
= x[n] - f(x[n])/f'(x[n]) [6]
which is Newton's formula (at last...).
So we multiply our function by a constant designed to put the graph of \(g(x)\) right in the middle of the “good” region, and that “invents” Newton’s method.
For example, let’s go back to the equation we worked with last time, \(\sin(x)-0.7031x=0\). We could conceivably put this in the form \(g(x)=x\) just by adding x to our function, taking $$g(x)=x+(\sin(x)-0.7031x)=\sin(x)+0.2969x$$ and iterating it. Here is what that would look like:
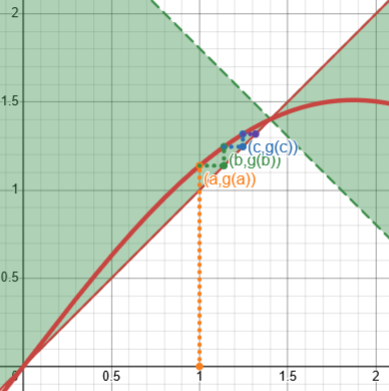
That’s tolerable, but not impressively fast.
But if we instead divide the function by the negative of its derivative first, we get $$g(x)=x-\frac{\sin(x)-0.7031x}{\cos(x)-0.7031},$$ and its iteration looks like this:
Now the graph is horizontal at the solution, so once we get close enough (which didn’t happen here until our second step!), it converges as fast as it can.
One more step: We want to examine how Newton’s method converges, in light of what we’ve learned about iteration.
We can now reverse the argument. Starting with Newton's formula, we write it in the form [2], with:
g(x) = x - f(x)/f'(x)
Note that (at least, if f'(x) is not zero), any solution of x = g(x) is a solution of f(x) = 0.
As we have seen, this will give a convergent sequence if (but not only if) there is a neighborhood of the solution a and a positive L < 1 such that |g'(x)| < L in that neighborhood. We compute g'(x):
g'(x) = 1 - ((f'(x)^2) - f(x)f"(x))/(f'(x)^2)
= f(x)f"(x)/(f'(x)^2) [7]
and the sequence will converge if there is a neighborhood of a such that this is between -L and +L, for some L < 1. If f' and f" are sufficiently well-behaved, there is no problem finding such a neighborhood, since, for x close to the root, f(x) will be very small.
So we don’t have a necessary condition for Newton’s method to converge, but we do have a condition under which we can be sure it will (if we start close enough): $$\left|\frac{f(x)f”(x)}{(f'(x))^2}\right|<L<1\text{ in some neighborhood}$$
Back to the original questions: cube root and arctan
How about the case that William said never converges?
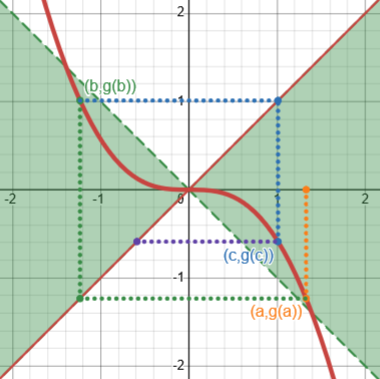
The problem with the equation x^(1/3) = 0 is that we have: f(x) = x^(1/3) f'(x) = x^(-2/3)/3 f"(x) = (-2/9)x^(-5/3) g'(x) = f(x)f"(x)/f'(x)^2 = -2 and this is < -1 for all x, which means that we cannot conclude that the sequence is convergent. In fact, as noted before, this implies that the sequence will always be divergent, because the inequality holds for all x. Intuitively, this comes from the fact that f"(x) tends to infinity faster than f'(x)^2. We have: f"(x)/f'(x)^2 = -2x^(-1/3)
Here is how iteration for the cube root fails to converge, starting from 0.2:
Since \(\displaystyle g(x)=x-\frac{\sqrt[3]{x}}{\frac{1}{3}x^{-2/3}}=-2x\) as shown, it is never in the “good region”.
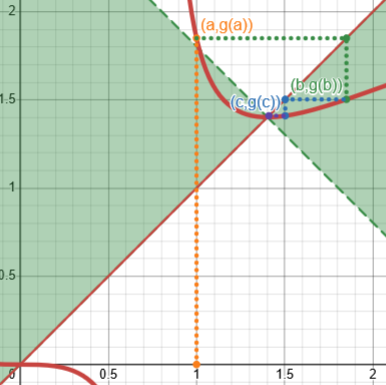
Now let’s look at the first equation William asked about, \(\arctan(x)=0\). The formula for Newton’s method is $$g(x)=x-\frac{f(x)}{f'(x)}=x-\frac{\arctan(x)}{\frac{1}{1+x^2}}=x-(1+x^2)\arctan(x),$$ so $$x_{n+1}=x_n-(1+x_n^2)\arctan(x_n)$$
Here is the graph of g, showing how the iteration converges, starting at 1.33:
We can see that the curve leaves the “good region” at \(x\approx1.39175\), supporting William’s observation that Newton’s method converges “within about 1.39″.
Where is our condition true for this function? Given that \(f(x)=\arctan(x)\), $$f'(x)=\frac{1}{1+x^2}\\f”(x)=\frac{-2x}{(1+x^2)^2}\\\left|\frac{f(x)f”(x)}{(f'(x))^2}\right|=\left|\frac{\arctan(x)(-2x)(1+x^2)^2}{(1+x^2)^2}\right|=\left|2x\arctan(x)\right|$$ This turns out to be less than 1 when \(|x|<0.76538\), approximately.
This is not the same as the point where our g leaves the “good region”; rather, it’s where our g has a slope of -1. This interval \(|x|<0.76538\) is a subset of the interval where the process will converge. As has been repeatedly emphasized, it is not a necessary condition. The important thing is that there is some interval where Newton’s method converges.
On the positive side, there are cases where such an approach can lead to exceptionally fast convergence. See, for example:
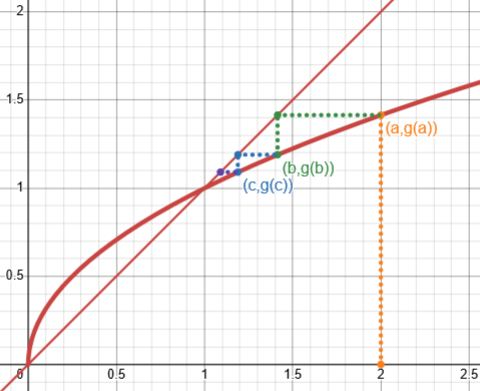
An Iterative Method of Calculating Pi
http://mathforum.org/library/drmath/view/65244.html
There, Doctor Jacques shows how you can very rapidly compute pi by iterating \(g(x)=x+\sin(x)\) starting with a rough estimate of 3, getting nine decimal places of accuracy after only two steps. This works faster that Newton.
