A couple recent questions involved errors made both by students and by the authors of their textbooks, involving trigonometric or inverse trigonometric functions. These offer some good lessons in pitfalls to be aware of.
Two wrong answers for a derivative
First, consider this question from Rahul in mid-August, comparing his own answer with the book’s:
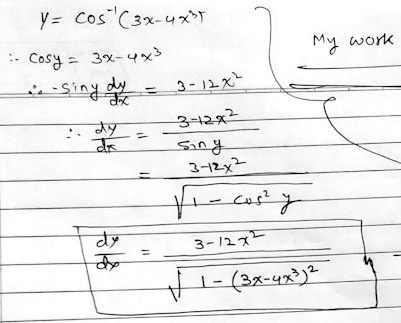
Please see my work in the attachment. My question is, I am not able to convert or simplify expression no. 1 into expression no. 2.
I believe both methods should give the same answer.
Please help.
The problem is to differentiate \(y=\cos^{-1}(3x-4x^3)\), but the main issue is not the calculus but the trigonometry and algebra. Rahul used implicit differentiation in a straightforward way, with a very small error; the book uses an unusual substitution to simplify the function, evidently inspired by a triple-angle formula, as we’ll see. If both are correct, there ought to be a way to algebraically show the equivalence of the answers. Can we do that?
Small error in the student answer
I answered:
Hi, Rahul.
First, have you tried expanding the first answer, and then trying to make the second answer look like the first, by multiplying the numerator and denominator by -(1-4x^2)? It does almost work. But check your work for the first method; you dropped a sign.
He took the cosine of both sides and then differentiated implicitly (much as, in logarithmic differentiation, we take the log of both sides to simplify things). The only problem is in dropping the negative in solving for dy/dx. There is no problem in taking the positive square root, because in the range of the inverse cosine, the sine is always positive. So the correct answer is $$\frac{dy}{dx}=\frac{12x^2-3}{\sqrt{1-(3x-4x^3)^2}}$$
Doing what I suggested, we can expand this to $$\frac{dy}{dx}=\frac{12x^2-3}{\sqrt{1-9x^2+24x^4-16x^6}}$$
Trying to make the other answer look like this, we get $$\frac{-3}{\sqrt{1-x^2}}\cdot\frac{1-4x^2}{1-4x^2}=\frac{-3(1-4x^2)}{\sqrt{(1-x^2)(1-4x^2)^2}}=\frac{12x^2-3}{\sqrt{(1-x^2)(1-8x^2+16x^4)}}=\frac{12x^2-3}{\sqrt{1-9x^2+24x^4-16x^6}}$$ which is the same answer!
But do you see a restriction hidden here? If \(1-4x^2\) is negative, then it is not equal to the square root of its square, and our work changed the sign. So the two expressions are only equivalent for \(x\in(\frac{1}{2},\frac{1}{2})\).
Big error in the book’s answer
But, also, there are some problems with the second method:
First, the assumption that x is the sine of an angle restricts the domain (at least in principle).
Second, in combining functions, they’ve ignored range issues. I’m guessing, since you say it comes from a book, that there is some context that provides both a reason for doing something so odd, and a justification for their assumptions.
So, from the start, this work is valid only for \(x\in[-1,1]\), since only then can we make the substitution at all. It would be valid if the problem specified, or implied, that condition. That doesn’t imply the answer is wrong, but it is suspect.
But also, the inverse cosine only cancels the cosine as shown when the given angle is in the range of the inverse cosine, so the fifth line assumes that \(0\le\frac{\pi}{2}-3\theta\le\pi\), requires that \(-\frac{\pi}{6}\le\theta\le\frac{\pi}{6}\), so that \(-\frac{1}{2}\le x\le\frac{1}{2}\). This is discussed in Mixing Trig and Inverse Trig Functions and More On Mixing Trig Functions.
I suspect that all this was done just to show off what can be done if you see a shortcut, in this case recognizing that the polynomial argument \(3x-4x^3\) is reminiscent of the triple-angle formula \(\cos(3\theta)=3\cos^3(\theta)-3\cos(\theta)\). Instead, it’s a demonstration of the danger in rushing through any work involving inverse trig functions! When you have a wonderful trick to show, don’t let it trick you!
Behind the scenes
But we can also just graph the various functions involved. This is often a good quick check (now that graphing is easy!).
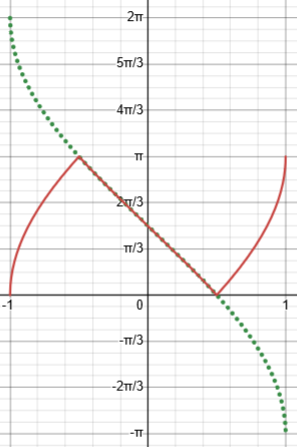
First, here are the original function, y = arccos(3x-4x^3) in red, and the supposedly equivalent y = pi/2 – 3 arcsin(x) in green:
Notice that they reverse direction for some inputs. Think about why.
This exactly fits my observations about unstated assumptions. The first part of the book solution is not a valid simplification of the given function.
Now, here are the two derivatives you want to make equal, #1 in red and #2 in green [after my correction]:
Again, these differ in sign for some values. Think about why. In particular, do the graphs of the derivative(s) look like the slopes of the original function(s)?
I’d like to see what the book says, and what the context is.
The little vertical lines are an artifact of the way Desmos graphs jump discontinuities; it should really look more like this:
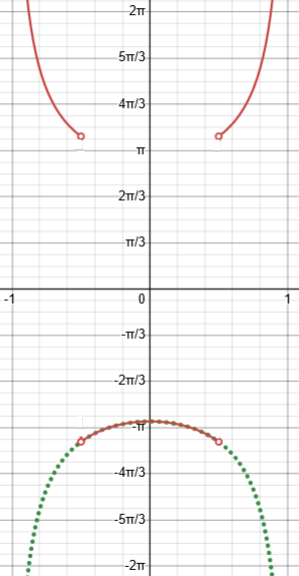
We can see that the actual derivative, in red, suddenly changes its sign at \(x=\pm\frac{1}{2}\) because the function “bounces” to stay in the range of the inverse cosine; the simplified version, in green, misses this.
Two wrong answers for a range
A few days later, we got this question from Debarghya:
Dr. I have seen the following problem:
If A = sin(cos x) + cos(cos x). The least and greatest value of A are
- a) 0 and 2 b) -1 and 1 c) -√2 and √2 d) 0 and √2.
My solution does not match with the options. Moreover, I don’t understand the solution given in book, because they have not considered range of inside function cos x which is restricted from [-1, 1]. Plz help.
My solution:
Book’s solution:
The correct answer is not one of the provided choices; both solutions have errors.
Error in the book’s answer
I answered:
Hi, Debarghya.
Interesting problem! Both your answer and the book’s are wrong.
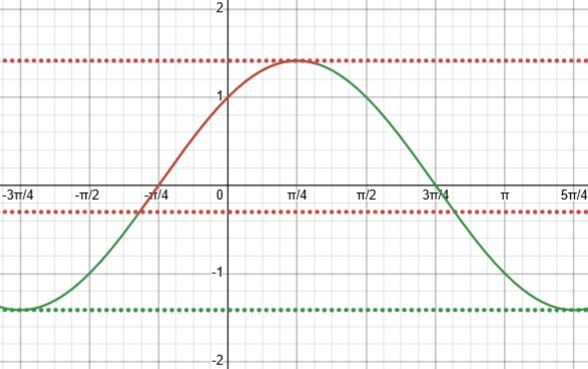
Theirs is wrong for the reason you state: They fail to consider that the argument of the outer cosine is restricted to [-1 – π/4, 1 – π/4], so that the cosine does not reach both of its extreme values. Here is a graph of cos(u) + sin(u) = √2cos(u – π/4), restricted to this domain (in red), showing its range (dotted red), and the unrestricted lower bound (dotted green):
The book found the range of the unrestricted function, between the highest and lowest lines shown (from \(-\sqrt{2}\) to \(\sqrt{2}\)), evidently forgetting that what I called u is a cosine, and can’t cover all the inputs needed to attain that entire range.
Since 1 – π/4 > 0, 0 is included in the domain of u, and the cosine does reach its maximum of 1; but since -1 – π/4 > -π, -π is not included, and the cosine does not reach its minimum of -1. Rather, the minimum value of the range is √2 cos(-1 – π/4) = -0.301…
As shown in the red part of the graph, \(u=\cos(x)\) ranges from \(-1\) to \(1\), so the argument of the outer cosine ranges from \(-1-\frac{\pi}{4}\), which does not extend back to its minimum, to \(1-\frac{\pi}{4}\), which takes it past its maximum.
Error in the student answer
Debarghya had two errors, one minor and the other important:
On the other hand, you made the opposite mistake: You used the sine rather than the cosine, which is not a problem; but you made a sign error, so that where you wrote √2 sin(cos(x) – π/4), you should have √2 sin(cos(x) + π/4). Fixing this, your work would yield
√2 sin(-1 + π/4) ≤ f(x) ≤ √2 sin(1 + π/4)
So the correct work would be $$f(x)=\sin(\cos(x))-\cos(\cos(x))\\=\sqrt{2}\sin\left(\cos(x)+\frac{\pi}{4}\right)$$ and when the cosine is at its lowest and highest values, $$f(x)=\sqrt{2}\sin\left(\pm1+\frac{\pi}{4}\right)$$
But here’s the big error: Because the sine is not monotonic, you can’t just take the sine of every term in an inequality. Your (corrected) lower limit would be correct (in contrast to theirs), namely √2 sin(-1 + π/4) ≈ -0.301. But because 1 + π/4 > π/2, the sine has turned downward before the upper limit of the domain, and the maximum value is just the max of the unrestricted function, namely √2 ≈ 1.414, rather than √2 sin(1 + π/4) ≈ 1.381.
We saw this in the graph above.
The issue of applying a monotonic function (one that is always increasing, or always decreasing) to an inequality was discussed in Monotonic Functions, Inequalities, and Optimization, where we said
If a function g is a monotonically increasing function, then a value of x that (locally/globally) (minimizes/maximizes) f(x) also (locally/globally) (minimizes/maximizes) g(f(x)), and vice versa.
This is because the greatest output of such a function corresponds to the greatest input. The present problem illustrates the fact that this is not necessarily true for a non-monotonic function.
The correct answer
Here is the actual graph of sin(cos(x)) + cos(cos(x)), with the actual limits of the range (red dots) and the incorrect upper limit, √2 sin(1 + π/4) (green broken line), which is actually the y-intercept rather than the maximum:
So the correct answer is not one of the choices, but also is not your answer, but rather
√2 sin(-1 + π/4) ≤ f(x) ≤ √2
I think their errors are more serious than yours! But at least their answer contains the actual range, so they haven’t excluded any values that are attainable…
Debarghya replied:
Yes … I understood my mistake. The sign error was just a silly one but the conceptual mistake that I committed was serious … since sine is not monotonic so it comes down after π/2 and the value of sin at (1+ π/4) must be lesser than that at π/2. yes…i got the point…thanks dr.
Inverse trig ranges strike again
Finally, here is another question from Debarghya that has several interesting features:
Dr. I have got a question from a book by A Dasgupta on inverse trigonometric function. I have solved the problem alright. but during the solution suddenly I observed an anomaly in finding the value of arcsin(sin 2θ) when 2θ belongs to [-π, -π/2].
When I use inequation to get the angle I find [-2θ – π]. but if I try to use reference angle and quadrant to find same angle I get [π – 2θ]. Why this anomaly? I am not comfortable with -ve [negative] angles. Perhaps the problem lies in handling -ve angles while finding reference angle.
My solution:
But my question is, when we evaluate any composite inverse trig function for an angle outside principal domain, such as sin-1(sin(2θ)) for 2θ in [-π, -π/2] then we do as follows:
sin-1(sin(2θ))
⸫ Reference angle, α = -π – (-2θ) = 2θ – π
In third quadrant sine is -ve.
⸫ In the interval [-π/2, -π/2] the sine function lies in 4th quadrant where angle is -ve.
⸫ sin-1(sin(2θ)) = -(2θ – π) = π – 2θ
Here we get the angle (π – 2θ) whereas in the problem (at *) we got the angle (-2θ – π). Why this anomaly?
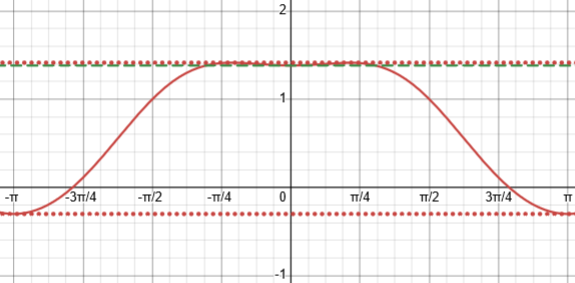
The problem involves the function $$2\tan^{-1}(x)+\sin^{-1}\frac{2x}{1+x^2}$$
Just as I would do in solving an equation with this expression, he first “gives a name to” one of the two angles involved, namely \(\theta=\tan^{-1}(x)\), so that \(\tan(\theta)=x\) and \(x\) is in the range of the inverse tangent, namely \((-\frac{\pi}{2},\frac{\pi}{2})\). Then he observes that $$\sin^{-1}\frac{2x}{1+x^2}=\sin^{-1}\frac{2\tan(\theta)}{1+\tan^2(\theta)}=\sin^{-1}(\sin(2\theta))$$
This involves a fact I had only recently become aware of, through a question from another user in India, Kalyan. When I first saw something like this, I thought it was an error, since $$\sin(2\theta)=\frac{2\tan(\theta)}{1+\tan^2(\theta)}$$ looks so much like $$\tan(2\theta)=\frac{2\tan(\theta)}{1-\tan^2(\theta)}$$ which is familiar to me. But the former is indeed true: $$\sin(2\theta)=2\sin(\theta)\cos(\theta)=2\frac{\sin(\theta)}{\cos(\theta)}\cos^2(\theta)=\frac{2\tan(\theta)}{\sec^2(\theta)}=\frac{2\tan(\theta)}{1+\tan^2(\theta)}$$ In fact, it is listed in Wikipedia, and is (in part) the basis for the powerful tangent half-angle substitution method of integration. It’s worth knowing!
So now the function has become $$2\theta+\sin^{-1}(\sin(2\theta))$$ and we want to simplify the second term. But \(2\theta\) can be anywhere between \(-\pi\) and \(\pi\), so \(\sin^{-1}(\sin(2\theta))\) is not necessarily equal to \(2\theta\); to handle this, he considers several separate cases. And it turns out that in two of the three, the function is constant.
I answered:
Hi, Debarghya.
First, I find the problem itself a little odd:
If \(\displaystyle 2\tan^{-1}x+\sin^{-1}\frac{2x}{1+x^2}\) is independent of x, then …
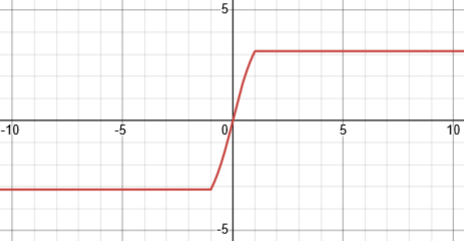
My best interpretation is that they are asking what domain you could restrict it to so that it would be constant. Here is its graph:
As you found, it is constant on either (-∞, -1] or [1, ∞), so none of the choices is a complete answer; both (a) and (c) are correct, but it doesn’t appear that you can choose both. It would be wrong to say it is constant on (-∞, -1] ∪ [1, ∞), as you did, since on that domain it takes two different values, so it is not independent of x.
Your work for the problem is good.
Finding \(\sin^{-1}(\sin(2\theta))\)
Let’s look at his three cases visually, before answering his concern.
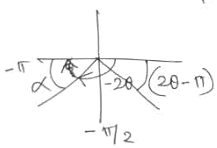
(i) \(2\theta\in\left(-\pi,-\frac{\pi}{2}\right]\)
If the angle is in the third quadrant, we want the angle in the fourth quadrant with the same sine (y-coordinate):
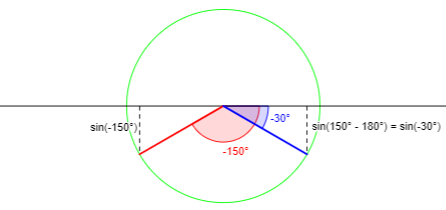
See below for details!
Here \(\sin^{-1}(\sin(2\theta)=-\pi-2\theta\), so $$2\theta+\sin^{-1}(\sin(2\theta))=2\theta+(-\pi-2\theta)=-\pi$$ is constant.
(ii) \(2\theta\in\left(-\frac{\pi}{2},\frac{\pi}{2}\right)\)
If the angle is in the first or fourth quadrant, then it is the inverse sine already:
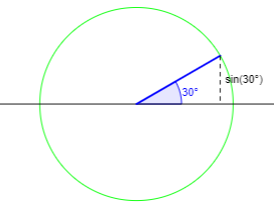
Here \(\sin^{-1}(\sin(2\theta))=2\theta\), so $$2\theta+\sin^{-1}(\sin(2\theta))=2\theta+2\theta=4\theta=4\tan^{-1}(x)$$ is not constant.
(iii) \(2\theta\in\left[\frac{\pi}{2},\pi\right)\)
If the angle is in the second quadrant, we want the angle in the first quadrant with the same sine (y-coordinate):
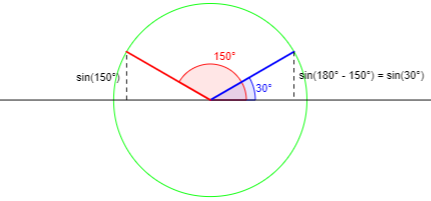
Here \(\sin^{-1}(\sin(2\theta))=\pi-2\theta\), so $$2\theta+\sin^{-1}(\sin(2\theta))=2\theta+(\pi-2\theta)=\pi$$ is constant.
For some similar issues and explanations, see Subtleties of Inverse Trig Functions.
Using reference angles in quadrant III
Now for your own question:
But my question is when we evaluate any composite inverse trig function for an angle outside principal domain, such as sin-1(sin(2θ)) for 2θ in [-π, -π/2] then we do as follows:
sin-1(sin(2θ))
⸫ Reference angle, α = -π – (-2θ) = 2θ – π
In third quadrant sine is -ve.
⸫ In the interval [-π/2, -π/2] the sine function lies in 4th quadrant where angle is -ve.
⸫ sin-1(sin(2θ)) = -(2θ – π) = π – 2θ
Here we get the angle (π – 2θ) whereas in the problem (at *) we got the angle (-2θ – π). Why this anomaly?
The error I see is in your calculation of the reference angle. Note that if 2θ is in [-π, -π/2], then 2θ – π is in [-2π, -3π/2], so that can’t be the reference angle, which must be a positive acute angle. Furthermore, your answer, π – 2θ, is in [3π/2, 2π], which is not the range of the inverse sine, so it is clearly wrong.
Looking at your sketch,
observe that the reference angle, α, is the positive angle between the given angle and the nearest half of the x-axis, which in this case means from the lower number, -π, to the larger number, 2θ. (NOT -2θ as you marked it!). So we subtract the lower from the greater, 2θ – (-π) = 2θ + π. For example (using degrees to keep the numbers simple), if 2θ = -150°, then the reference angle is 2θ + 180° = -150° + 180° = 30°, which is in the correct interval.
When you then use -α as the inverse sine, that gives the correct -2θ – π.
The example is what I showed above for case i.
We discuss related ideas in
Mixing Trig and Inverse Trig Functions
Specifically, in the section “Inverse trig(trig)”, I say that I read “arccos(cos(θ))” as “the angle in [0, π] whose cosine is the cosine of θ.” For the present question, I read “arcsin(sin(2θ))” as “the angle in [-π/2, π/2] whose sine is the sine of 2θ.” To find this angle, we want to reflect the given angle across the y-axis (so that the y-coordinate remains the same), which we do by subtracting from -π. That gives the answer you got (correctly), in the form -π – 2θ.
But I will admit that I generally have to check my thinking several times to get it right! Negatives always make things harder.
One thing I do to check my thinking is just what I did here, seeing that the result is in the right interval, and also using a numerical example.
Working with negatives
Debarghya replied,
Thanx a lot dr. for your patience and explanation. I have understood the things you mentioned. but why I wrote -2θ I want to explain. I think my problem lies in interpreting -ve values.
In any problem if we specify a +ve quantity by a variable x then in the same problem to denote same quantity but with -ve value we always use -x. Am I right?
If I am right then when the angle 2θ was in 2nd quadrant and between [π/2, π] we had used 2θ. but when same quantity has become negative then we have to use -2θ. in that case when 2θ = 150° then as per my notation the angle in -ve direction becomes -150° and hence reference angle is π -2θ = 180° – 150° = 30° and same result obtained.
The confusion is due to the fact that I am using the notation 2θ for +ve values (and hence -2θ for -ve case) and you are using 2θ for all angles (+ve or -ve).
If \(x\) is positive, then \(-x\) is negative; that is true. But if \(2\theta\) is negative, it must still be called \(2\theta\)!
I responded:
You ask,
In any problem if we specify a +ve quantity by a variable x then in the same problem to denote same quantity but with -ve value we always use -x. Am I right?
The negative sign does not mean “this number is negative”, but “the opposite of this number”. If x > 0, then -x < 0. But if x < 0, then -x > 0. So x can represent a negative number, and -x is not necessarily negative.
If I am right then when the angle 2θ was in 2nd quadrant and between [π/2, π] we had used 2θ. but when same quantity has become negative then we have to use -2θ. in that case when 2θ = 150° then as per my notation the angle in -ve direction becomes -150° and hence reference angle is π – 2θ = 180° – 150° = 30° and same result obtained.
You’re asking for “arcsin(sin 2θ) when 2θ belongs to [-π, -π/2]”. This means that 2θ < 0, implying that θ < 0. In this case, -2θ would be positive.
An example of this case would be 2θ = -150°, so that π – 2θ = 180° – (-150°) = 330°. That is not a valid reference angle.
The confusion is due to the fact that I am using the notation 2θ for +ve values (and hence -2θ for -ve case) and you are using 2θ for all angles (+ve or -ve).
Your usage is non-standard, and will lead to great confusion in communicating with others. The variable θ must be allowed to have either sign.
For some relevant thoughts, see Talking About Negative Numbers.
Negative numbers are risky; I try to slow down and check every detail whenever I work with negative numbers.

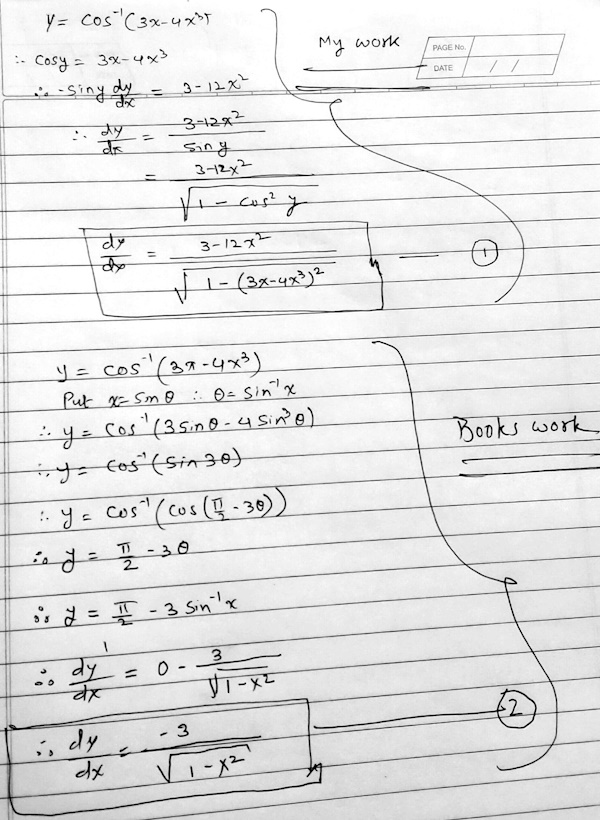
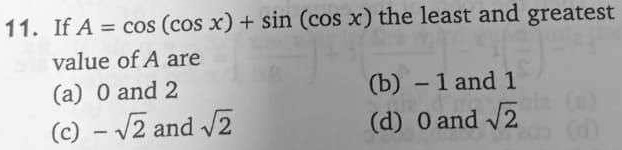

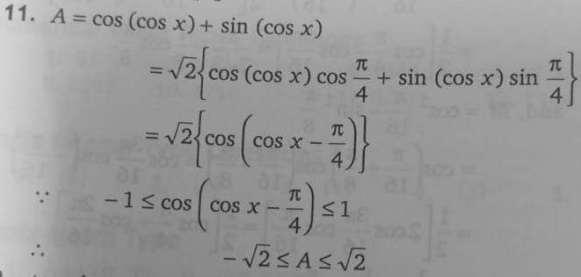

Pingback: Inverse Trig Problems With Unstated Restrictions – The Math Doctors