In discussing the value of radians, we introduced the idea that trig functions are easier to evaluate that way. That raises the question, how do you find the value of a trigonometric function without a calculator, and how do calculators themselves do it? Let’s look into that.
Three methods
We’ll start with a general question, from 1999:
Methods of Computing Trig Functions Hello, I'm trying to understand something. The book says "In right triangle ABC, with A as the right angle: tan(C) = c/b" To find the angle C if I know the lengths of 2 sides (b = 3, c = 4), I can use tan(C) = c/b = 4/3 = 1.33. Without using the tables at the back of the book, what would I do next to figure out the actual angle of C when I know tan(C) = 1.33? Thank you.
If you haven’t seen one (since we use calculators much more these days), here is an example:
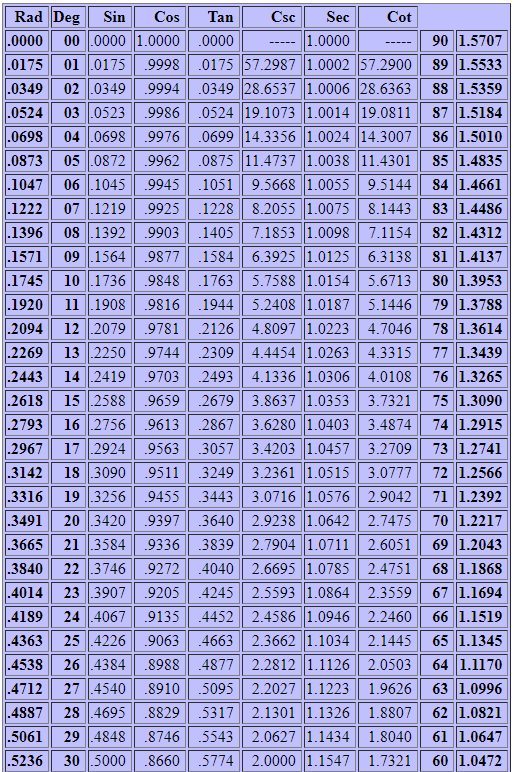
But when they were really needed, they were more precise; here is the start of the one I used in college (taking 22 pages in CRC Standard Mathematical Tables):

This is for angles in degrees and minutes; the first page of the table covers 0 to 2 degrees. There was also a table for tenths of a degree, and another for radians (through 2 radians).
But what could you do without a table?
Doctor Rick answered:
Hi, David. I'm not sure exactly what your problem is, but I think you're thinking, "What good does it do to define this thing called a tangent, if all I can do with it is look up the answer in a table? I haven't learned anything if I have to look up the answer every time!" Another way to put it: "So how did they come up with the numbers in that table, anyway? And why don't they teach us that?" The fact is, it's not easy to make those tables; in centuries past, people devoted a good part of their lives to calculating the numbers in the table by hand. And now that we have computers, the methods used to compute trig functions (in computers or scientific calculators) make use of things you won't learn for a while yet. But it's good to learn enough about these methods to appreciate the fact that you have tables and calculators. So here is something I wrote for another student who wondered how one can calculate a trig function by hand. I hope it helps you a little.
This is the goal of this post: Not to teach you how to find an inverse tangent or a sine by hand for your next problem, but to show that it isn’t magic – though it isn’t something you’ll want to do more than once!
Before we had calculators, we either looked up the answer in a book of tables (I still have mine) or we used a special scale on a slide rule, which is essentially a table on a stick. That begs the question: How were those tables calculated? I know of three methods. I must admit I have never used any of them! A few people dedicated their lives to doing the calculations and putting the results in tables, and the rest of us bought the tables so we could spend our lives doing other things.
We’ll do a couple examples here. But I, too, have never done this as part of solving a bigger problem.
Make a table like Ptolemy’s
METHOD 1: The first "trig table" was produced by Ptolemy of Alexandria, Egypt, in the second century AD. It was part of a book called the Almagest, a name given to an Arabic translation, from its Greek nickname "the greatest." This book was used by astronomers for 1000 years. To construct the tables in the Almagest, Ptolemy started with some angles that can be calculated using geometry. He could have used 30 degrees (whose sine is 1/2), but he instead chose to use 36 degrees, whose sine can be found from the construction of a regular pentagon. Then Ptolemy used the equivalent of our half-angle formulas in trigonometry. He repeatedly divided the angle in half until he got a figure for the sine of 1/4 degree. Finally, he built up the sines and cosines of all the angles in steps of 1/4 degree by using the equivalent of our trigonometric sum and difference formulas, which he came up with.
In case you’re interested, here is the start of Ptolemy’s table:

This gives the chord length (given a 60-unit radius, written in sexagesimal notation), \(120\sin\left(\frac{\theta}{2}\right)\), for angles from \(\frac{1}{2}^\circ\) to \(6^\circ\), and is explained here. The method of construction is explained elsewhere in the same article.
Use the Taylor series
METHOD 2:
If you want to compute the sine of an angle without computing a whole table full of angles, you can use the second method: a formula called the Taylor series expansion of sin(x). You won't learn how to derive this formula until you take calculus, but it isn't hard to write down:
3 5 7 15 17
x x x x x
sin(x) = x - --- + --- - --- + ... - --- + --- ...
3! 5! 7! 15! 17!
where, for instance, 5! (5 factorial) is 5 * 4 * 3 * 2. The series goes on forever, but if x is between 0 and pi/2 (and that's really all you need), this many terms (9 of them) gives an answer as good as most calculators.
As an example, $$\sin\left(\frac{\pi}{6}\right)=\sin\left(0.5236\right)=0.5236-\frac{0.5236^3}{6}+\frac{0.5236^5}{120}-\frac{0.5236^7}{5040}+\dots\\=0.5236-0.0239+0.000328-0.000005=0.5000$$
We can stop there because subsequent terms won’t add enough to matter.
There are Taylor series for cos(x) and arctan(x), also:
2 4 6 14 16
x x x x x
cos(x) = 1 - --- + --- - --- + ... - --- + --- ...
2! 4! 6! 14! 16!
3 5 7
x x x
arctan(x) = x - --- + --- - --- + ..., where |x| < 1
3 5 7
If |x| > 1, compute arctan(x) = pi/2 - arctan(1/x). The arctangent formula, unfortunately, converges VERY slowly near x = 1 (you'd need a huge number of terms), so it's not very useful as it stands.
The tangent, of course, can be calculated from the sine and cosine. The inverse sine and cosine can be computed from the inverse tangent:
arcsin(x) = arctan(x/sqrt(1-x^2))
arccos(x) = pi/2 - arctan(x/sqrt(1-x^2))
We’ll be seeing more about the arctan function.
If you’re a calculator, use CORDIC
METHOD 3: There is a way that takes less calculation than the Taylor series. It's called the CORDIC algorithm, and it requires computing about 100 numbers and storing them in the calculator's memory - something it can do, but you and I wouldn't like so much. Also this method is easier when you work with binary numbers, which calculators do but you and I don't. So for people, the Taylor series method would probably be better, but for calculators the CORDIC method is a snap. What I haven't seen yet is how computers calculate the inverse tangent.
We’ll see a little more about this below; more powerful computers have more powerful methods, but this may still be used for calculators.
So those are the three methods I know of: - Ptolemy's method of building a table using half-angle and sum and difference formulas; - the Taylor series method to calculate one sine or cosine with a nice formula; - the CORDIC method that calculators use. I still prefer a calculator or a table, but it is satisfying to know how I COULD do it myself if I had to.
More about CORDIC
This question is from 1996, and was probably my first introduction to CORDIC:
Calculators and Trig Functions I have read through your archives and found that the only way you present to solve a trigonometric function, for example, sin (.78539), is through a complicated formula: sin(.78539) = .78539 - .78539^3/3! + .78539^5/5! - .78359^7/7! ... Is there no simpler way to do this? It doesn't seem logical to me that a calculator could do this as fast as it does, especially without a radian measure to start with. I understand the principle of the unit circle, and was wondering if there was a way (possibly outside the realm of trigonometry into calculus) to determine the y value on a graph of the arc subtended by the angle theta. This gives the value of sine as 1/y (1 divided by the height arc in relation to the x-axis). I have asked teachers at my school, but none could make it clear to me. Perhaps you can help. I only ask about sine because, after reading some of the other letters here, I realized that the other functions can be derived from sine.
Calculators can, in fact, do this sort of (Taylor series) calculation rapidly, and the conversion from degrees to radians with no trouble; but efficiency is in fact an issue. So another way is used.
Doctor Jerry answered:
Hi Jared, I recently went to a mathematics conference at which Prof. Bruce Edwards gave a paper titled "How Do Calculators Calculate." Here are the first sentences of his paper: "How do calculators quickly produce the values of transcendental functions? For instance, how does the TI-85 calculate tan 1.5? The calculator does not use series or polynomial approximations, but rather the so-called CORDIC method." I'll try to give a short description of the CORDIC method, but you may want to refer to the paper by Charles W. Schelin, "Calculator Function Approximation", _American Mathematical Monthly_, 1983, pp 317-325.
The first paper appears to be here (from 1997); the second is here, but requires access. The name CORDIC stands for “COordinate Rotation DIgital Computer”.
To calculate the sine and cosine of a number t, we first need to clarify some notation. We use x_{k} to mean x sub k; x_{k+1} would mean x sub k+1; and so on. Also, x^k means x to the power k; x^{k+1} means x to the power k+1. For -pi/2 <= t <= pi/2, let :
x_{k+1} = x_k - d_k*y_k*2^{-k}
y_{k+1} = y_k + d_k*x_k*2^{-k}
z_{k+1} = z_k - d_k*arctan(2^{-k}).
The constants arctan(2^{-k}) are stored in the calculator. I don't know how many of these are stored, but judging from Edwards' comments, it might be something like
e_k = arctan(2^{-k}) for k = 0,1,2,...,50.
In any case, if you want more accuracy, you need to store more of these constants. We also store the product
K = cos(e_0)*cos(e_1)*...*cos(e_{46}).
The choice of the number of factors in this product depends upon the accuracy wanted. The constants d_k are defined by d_k = sgn(z_k). The sgn function gives +1 for any number greater than or equal to 0 and -1 for any number less than 0.
That is, we define $$x_{k+1}=x_k-d_ky_k2^{-k}\\y_{k+1}=y_k+d_kx_k2^{-k}\\z_{k+1}=z_k-d_k\arctan\left(2^{-k}\right)\\d_k=sgn(z_k)$$ and store $$e_k=\arctan\left(2^{-k}\right)\text{ for }k=0,1,2,\dots,50\\K=\cos\left(e_0\right)\cos(e_1)\dots\cos\left(e_{46}\right)$$
To do the calculation, take x_0 = K, y_0 = 0, and z_0 = t.
Calculate x_1, y_1, and z_1 from the above formulas. Then calculate x_2, y_2, and z_2. Etc.
Note that only addition and multiplication are required.
With t = 1, after a while, one gets
x_{47} = 0.54030230586814,
y_{47} = 0.84147098480790,
z_{47} = 0.00000000000000.
The x and y values are the cosine and sine of 1 radian.
(Doctor Jerry wrote “x_0 = 1/K”, but I have changed it to “x_0 = K”, as stated in the paper, and that works for me.)
Each step is simple, so the calculator can quickly work through many of them. It’s much more efficient than the Taylor series, as good as that is, with basic hardware.
Here’s the whole process, done with a spreadsheet, where t is the input angle (gray parts would be precomputed and stored):
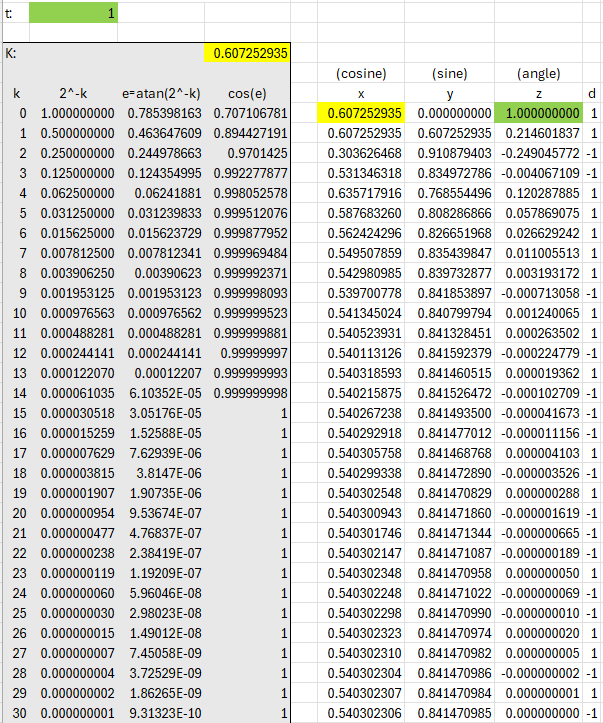
The last line shows that \(\cos(1)=0.540302306\) and \(\sin(1)=0.841470985\), both of which are correct to the 9 decimal places shown. The values don’t change after this.
For an explanation of the algorithm, in addition to the two papers mentioned, you can see Wikipedia.
More about series
This is from 2002:
Trigonometry by Hand I am the type of person who just has to know how everything works. I have been wondering for months how to do sines, cosines, tangents, arcsines, arccosines, and arctangents without using tables or a calculator. I have tried to figure out these formulas for months, but I cannot get anything to work. If you could tell me these formulas, I would be very pleased.
Doctor Rob answered, focusing on the series that Jared didn’t like:
Thanks for writing to Ask Dr. Math, Sam! For sin(x) and cos(x), where x is in radians, use the infinite series sin(x) = x - x^3/3! + x^5/5! - x^7/7! + x^9/9! - ... cos(x) = 1 - x^2/2! + x^4/4! - x^6/6! + x^8/8! - ... Take as many terms as you need to get the accuracy you desire. Then tan(x) = sin(x)/cos(x).
The series for the tangent is harder to describe, and does not work for all x.
Here are the sums of the first, first two, first three, and first four terms of the series for sine, compared with the actual sine, showing how well the series approximates the values:
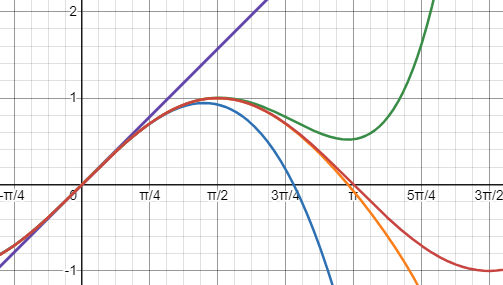
Similarly, here are the first, first two, first three, and first four terms of the series for sine, compared with the actual cosine:
Inverse trig functions
For arctan(y), if |y| < 1, use the infinite series arctan(y) = y - y^3/3 + y^5/5 - y^7/7 + y^9/9 - ... which gives you the angle in radians, again. If |y| > 1, then |1/y| < 1, and you can use the identity arctan(y) + arctan(1/y) = Pi/2. If |y| = 1, you can write down the answer by inspection.
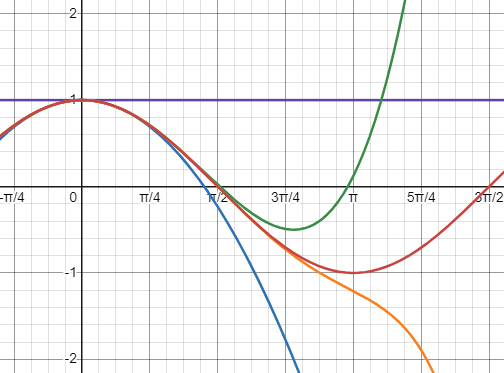
Again, here are the first, first two, first three, and first four terms of the series for sine, compared with the actual arctan:
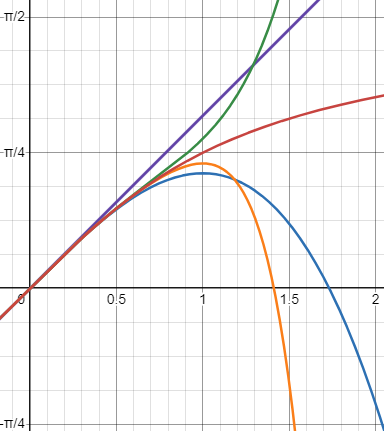
This doesn’t work very well at all for x larger than 1, or even close to 1; we’ll see how to make it practical, beyond the one trick offered here, below.
For arcsin(y) and arccos(y) with 0 < y < 1, you can use the facts that arcsin(y) = arctan(y/sqrt[1-y^2]), arccos(y) = arctan(sqrt[1-y^2]/y). If -1 < y < 0, then 0 < -y < 1, and there are the helpful identities arcsin(y) + arcsin(-y) = 0, arccos(y) + arccos(-y) = Pi. If y = -1, 0, or 1, you can write down the answer by inspection. The above series converge very rapidly for small values of x and y, but less so for large ones. You can ensure that the values of x you use in the first two series are between 0 and Pi/4 by applying various trigonometric identities relating sine and cosine values.
Examples below will illustrate this.
No, really, how do I find arctan using series?
In Finding Angles, Barry in 1996 had asked a question much like the question asked in our first question above; Jayme in 1997 wasn’t happy with the answer there (which was to use a calculator to find \(\arctan\left(\frac{b}{a}\right)\)):
Computing Angles of a Right Triangle From your archives: "How do you compute the other two angles of a right triangle? I know the hypotenuse and the other two lengths, but how do I get the other two angles?" The answer, from Dr. Tom, is "push the arctan button on your calculator"! Come on, I have neither a scientific calculator, nor a slide rule, nor a book of tables. Instead, I have my head and a pencil and paper. Is there a way to do this manually? If a table is required, where can I find it? Thanks.
Most likely Jayme either had one of those tools, or could find one online; but that felt unnecessary. So, could you do without the tables if you either had to, or just wanted to?
Doctor Rob answered:
There are tables in every book on trigonometry ever written. There are also tables in the Handbook of Chemistry and Physics (old) or the Chemical Rubber Company Tables (newer). If you insist on not doing it with tables, you can compute the arctangent function using Maclaurin series as follows: arctan(x) = x - x^3/3 + x^5/5 - x^7/7 + x^9/9 - ... (-1 < x < 1). If you truncate this series, the error will be less than the first omitted term. The answer will appear in radians, so you will need to multiply by 180/Pi to convert to degrees. Admittedly this involves quite a bit of calculation using pencil and paper, but it is feasible.
The Maclaurin series is just a specific kind of Taylor series, namely one that starts at zero, as most examples do.
For example, if you find that you need the arctangent of .32000, you can compute
x = .32000 x = .32000
x^2 = .10240
x^3 = .03277 -x^3/3 = -.01092
x^5 = .00336 x^5/5 = .00067
x^7 = .00034 -x^7/7 = -.00005
x^9 = .00004 x^9/9 = .000004
sum = .30970, accurate to 5 significant figures,
arctan(x) = .30970 radians,
= .30970*180/Pi = 17.745 degrees.
Note that, for efficiency, he doesn’t calculate each power of x directly, but finds the square, and then multiplies by that repeatedly to get all the odd powers.
But if x is near 1 …
The smaller x is, the faster this series converges. If x is very close to 1, so that the series converges too slowly, you can use the formula arctan(x) = 2*arctan[(sqrt[1+x^2]-1)/x], and the argument of the arctangent on the right is farther from 1 so that the Maclaurin series will converge faster. This process can be iterated. For very small values of x, arctan(x) = x is a good approximation.
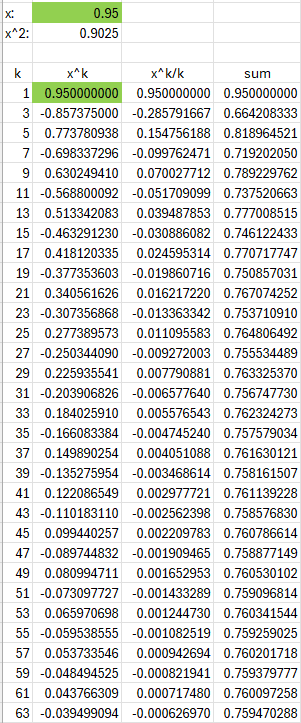
As an example of the problem, if we calculated the series for \(\arctan(0.95)\), we’d get $$x-\frac{x^3}{3}+\frac{x^5}{5}-\frac{x^7}{7}+\frac{x^9}{9}-\dots\\=(0.95)-\frac{(0.95)^3}{3}+\frac{(0.95)^5}{5}-\frac{(0.95)^7}{7}+\frac{(0.95)^9}{9}-\dots\\=0.95-0.28579+0.15475-0.09976+0.07002=0.78922$$ whereas the correct answer is 0.75976. In fact, we only have three significant figures after 30 terms:
But using the suggested formula, we have $$\arctan(x) = 2\arctan\left[\frac{\sqrt{1+x^2}-1}{x}\right]\\\arctan(0.95) = 2\arctan\left[\frac{\sqrt{1+(0.95)^2}-1}{0.95}\right]\\=2\arctan\left[0.39927\right]\\=2(0.37988)=0.75976$$
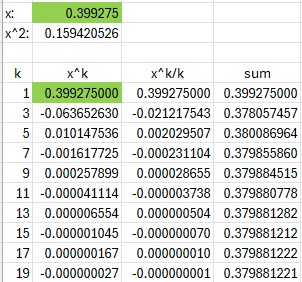
Applying the series to 0.39927 converges much faster:
If x is extremely close to 1, here is a method which is actually better: When x is near the tangent of an angle A you know, such as x near 1 and A = Pi/4, then you can do this: y = arctan(x), x = tan(y), tan(y-A) = [tan(y)-tan(A)]/[1+tan(y)*tan(A)], y = A + arctan([x-tan(A)]/[1+x*tan(A)]), arctan(x) = A + arctan([x-tan(A)]/[1+x*tan(A)]). The fraction inside the arctan on the right is quite small, and the convergence of the Maclaurin series is accordingly very fast. In the case where A = Pi/4, one is faced with finding the arctangent of (x-1)/(x+1), which is very small.
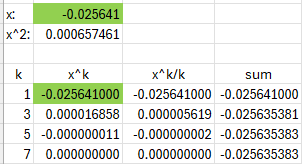
So you can take advantage of a couple known values to make the work even easier. In this case, again taking \(x=0.95\), we get \(\frac{x-1}{x+1}=\frac{0.95-1}{0.95+1}=-0.025641\), whose arctangent is -0.025635, so our answer is \(\arctan(0.95)=\frac{\pi}{4}+(-0.025635)=0.75976\); and this arctan converges in just four terms:
… and if x is large …
If your x > 1, then 1/x < 1, and you need to use the relation arctan(x) = Pi/2 - arctan(1/x).
For example, if we try to use the series to find \(\arctan(2)=1.1071\), this is what happens:
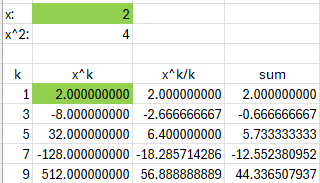
It doesn’t converge at all. But \(\arctan\left(\frac{1}{2}\right)=\arctan(0.5)=0.46364\), and \(\frac{\pi}{2}-0.46364=1.1071\). This, again, converges reasonably:
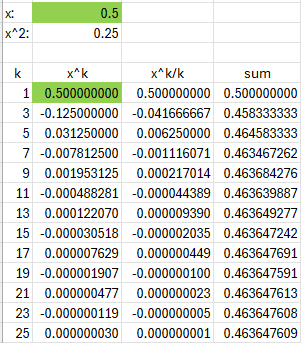
Today, there are many online calculators, or the one on your phone (which has a scientific mode, if you haven’t discovered it). But’s it’s still fun to know you could do it all “by hand” if you really wanted to.
